理想变压器的工作原理和应用

在研究分析变压器时，为了使问题的分析研究简单化和理想化，经常根据实际情况加以修改或补充。理想变压器是实际变压器的元件模型，是实际变压器的理想化模型，是对互感元件的理想科学抽象，是极限情况下的耦合电感。理想变压器的3个理想化条件如下。

（1）耦合电感无损耗，即线圈是理想的。

（2）理想变压器无漏磁通，即耦合系数k＝1，为全耦合。

（3）自感系数L1、L2和互感系数M无限大，且L1/L2为常数。

针对线性变压器而言，磁通与电流是线性关系，理想变压器是一种线性非时变元件。

以上3个条件在工程实际中不可能满足，但在一些实际工程概算中，在误差允许的范围内，把实际变压器当理想变压器对待，可使计算过程简化。

例8－7　在图8－24所示收音机电路中，输出变压器的作用是让扬声器阻抗和晶体管的输出阻抗匹配，从而驱动喇叭振动发出声音。已知信号源电动势E＝6V，内阻r＝100Ω，扬声器的电阻R＝8Ω。（1）计算直接将扬声器接到信号源上时的输出功率。（2）若用N1＝300匝N2＝100匝的变压器耦合，输出功率是多少？（3）若使输出功率达到最大，问匝数比为多少？此时输出功率等于多少？

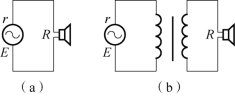
图8－24　例8－9题图

解题分析：这是一道变压器应用的实际例题，要想对其中的参数进行具体求解，首先要对变压器的基本性质进行学习。

理想变压器有3个重要特性。

（1）电压变换。

（2）电流变换。

（3）阻抗变换。

下面结合图8－25对理想变压器的3个重要特性进行一一分析。

图8－25　理想变压器特性分析示意图

（1）变压关系。

经推导可知理想变压器一次、二次线圈的匝数N1、N2与一次、二次线圈端电压成正比，即

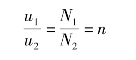
在正弦稳态下，电压相量关系为

式中　n——匝比或变比，是理想变压器的唯一参数。

（2）变流关系。

根据互感线圈的电压、电流关系（电流参考方向设为从同名端同时流入或同时流出），有

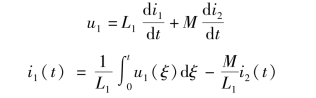
代入理想化条件，得

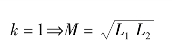
可以得出理想变压器的电流关系为

注意：理想变压器的变流关系与两线圈上电压参考方向的假设无关，但与电流参考方向的设置有关，若i1、i2的参考方向一个是从同名端流入，一个是从同名端流出，此时i1与i2之比为

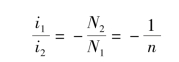
理想变压器的伏安关系统一可表示为

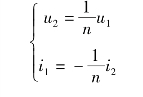(www.xing528.com)

或者写为相量形式，即

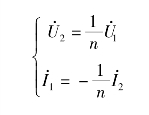
（3）变阻抗关系。

当理想变压器次级接阻抗为ZL的负载时，如图8－26（a）所示，由理想变压器的变压、变流关系可得一次侧的输入阻抗为

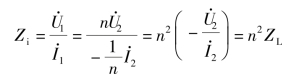
理想变压器输入端的等效阻抗与负载阻抗成正比，比例常数是变压器匝数比的平方。Zi称为二次侧对一次侧的折合等效阻抗，如图8－26（b）所示。

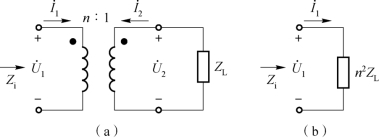
图8－26　理想变压器等效阻抗示意图

换言之，理想变压器具有变换阻抗的功能，二次侧折算到一次侧后，阻抗扩大了n2倍，而一次侧电流保持不变；一次侧折算到二次侧后，阻抗缩小到原来的1/n2。若负载为纯电阻RL时，一次侧的输入阻抗也变为纯电阻性，其值为

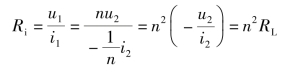
注意：理想变压器的阻抗变换性质只改变阻抗的大小，不改变阻抗的性质。

（4）传输能量。

由理想变压器的变压、变流关系得初级端口与次级端口吸收的功率和为

上式表明，理想变压器既不储能也不耗能，在电路中只起传递信号和能量的作用。如果在理想变压器的二次侧接上负载，则一次侧电源提供的功率将全部传输到负载上，即理想变压器本身消耗的功率为零。

通过上面的学习，下面对例8－7进行具体解析。

求解步骤如下。

（1）如图8－24（a）所示，当直接把扬声器接到信号源上时，输出功率为

（2）如图8－24（b）所示，当通过变压器耦合时，输出功率可利用变压器的输入等效电路来计算。从一次侧（输入等效电路）看，扬声器的一次侧输入阻抗为

输出功率为

（3）若使输出功率达到最大，要求扬声器的一次侧输入阻抗匹配。

练一练：已知某收音机输出变压器的原边匝数为600，副边匝数为30，原边原来接有16Ω的扬声器。现因故要改接成4Ω扬声器，问输出变压器的匝数N2应该改为多少？

综上所述，理想变压器是一种线性无损耗元件。它的唯一作用是按匝数比n变换电压、电流和阻抗，也就是说，表征理想变压器的参数仅仅是匝数比n。在实际应用中，用高磁导率的铁磁材料作铁芯的实际变压器，在绕制线圈时，如果能使两个绕组的耦合系数k接近于1，则实际变压器的性能将接近于理想变压器，可近似地当作理想变压器来分析和计算。

知识点归纳

理想变压器既不耗能又不储能，它将一次线圈输入的能量全部从二次线圈输出。在传输过程中，仅将电压、电流按变比作数值变换。理想变压器纯粹是一种变换信号和传输电能的元件。

理想变压器的特点如下。

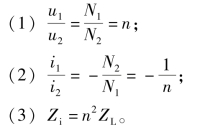
课后思考

（1）初级回路的阻抗能否反射到次级回路呢？如果能，请写出它的表达式。

（2）理想变压器和全耦合变压器有何相同之处？有何区别？

（3）试述理想变压器和空心变压器的反射阻抗不同之处。