只考虑一个方向上的风速,也就是10min平均风速的风向。考虑在10min内,具有常量U10和σU的风速过程U(t),它可以假设成是静态的。风速过程的谱密度表示了风湍流的能量是如何在各个频率之间分布的。有几个模型可以用来描述谱密度,最常见的谱密度模型是哈里斯(Harris)谱,即
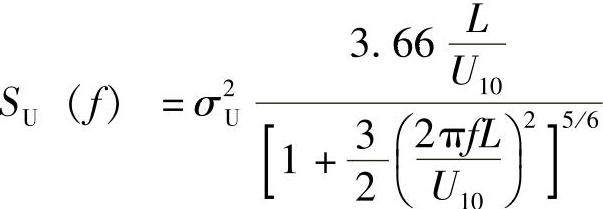
式中 f——频率;
L——特征长度,与积分长度尺度Lu有关,L=1.09Lu。
全尺寸数据校验表明,L的值在66~440m范围内,L≈200m用于与谱的高频部分匹配。根据经验,建议哈里斯谱不要用于低频范围,如f<0.01Hz时。
另一个比较常用的功率谱密度模型是凯莫尔(Kaimal)谱,即
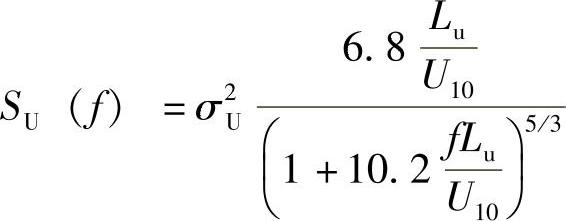
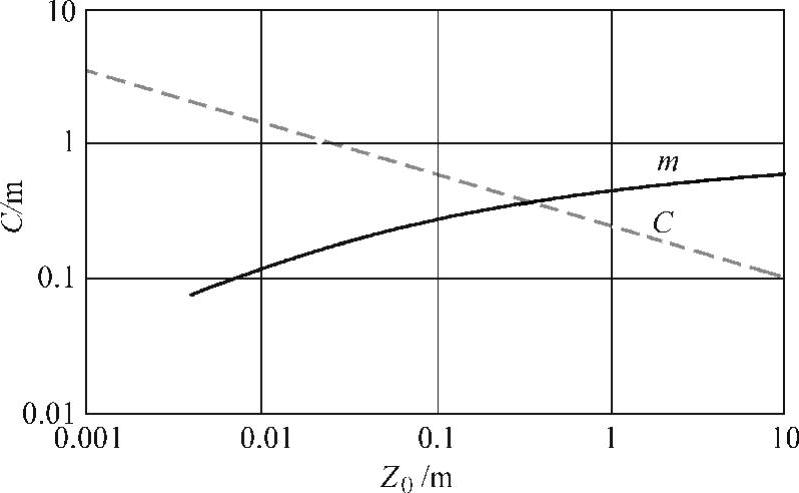
图3-4 凯莫尔谱积分长度尺度的系数C和m
上式中的积分长度尺度由L=100Czm给出,其中z是高度,C和m取决于粗糙长度z0,如图3-4所示,Eurocode1(欧洲规范1)使用该谱。
对于惯性尾部区域的高频,IEC61400-1要求设计所用的功率谱密度近似采用下面的形式:
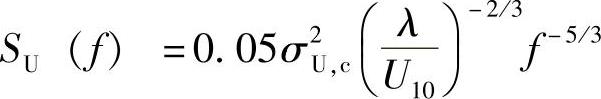
上式中的湍流尺度参数λ取决于地形高度z,即
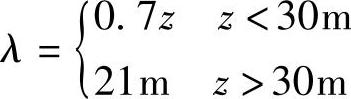
湍流尺度参数是由无量纲、纵向功率谱密度等于0.05时的波长定义的。
设计时,计算常常与轮毂高度的风条件有关,如U10和σU都是在轮毂高度上计算的。必须注意,湍流尺度参数λ与积分长度尺度L有关,L=4.76λ。IEC61400-1中所谓的凯莫尔谱由下式给出:
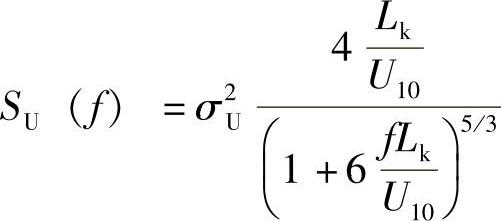
式中 Lk——Lk=8.1λ。
对于垂直和横向风速谱密度的计算,上式可以分别用σUy和σUz来代替σU,用λy=0.3λ和λz=0.1λ来代替λ。
必须注意,用上面的模型计算功率谱密度有一定的随机性。每个模型都理想化和简单化了,并且在一个有限的频率范围内为了提供一个好的数据拟合进行了校准。特别是在低频部分,模型显示出了很大的差异,图3-5给出了三种功率谱密度模型,可做无量纲尺度比较。(https://www.xing528.com)
谱矩对于表示风速过程U(t)是十分有用的,第j阶谱矩定义为

在如10min这样一段比较短的时间内,风速过程U(t)通常表示成一个由10min平均风速U10和标准偏差σU决定的高斯(Gaussian)过程。这个时间段给定点的任意风速U遵循由平均风速U10和标准偏差σU决定的正态分布。同质地形的湍流常常是这种情况,但是复杂地形的湍流很难得到-0.1的偏斜,这就意味着并不满足高斯假设。
注意,对于同质地形,虽然短期风速过程遵循高斯过程,但常常却并不是一个窄带的高斯过程,这是由谱密度导致的,这对预测极端风速是非常重要的。这样的极端值和它们的概率分布可以通过一系列的频矩来表示,请参见相关随机过程理论教科书。
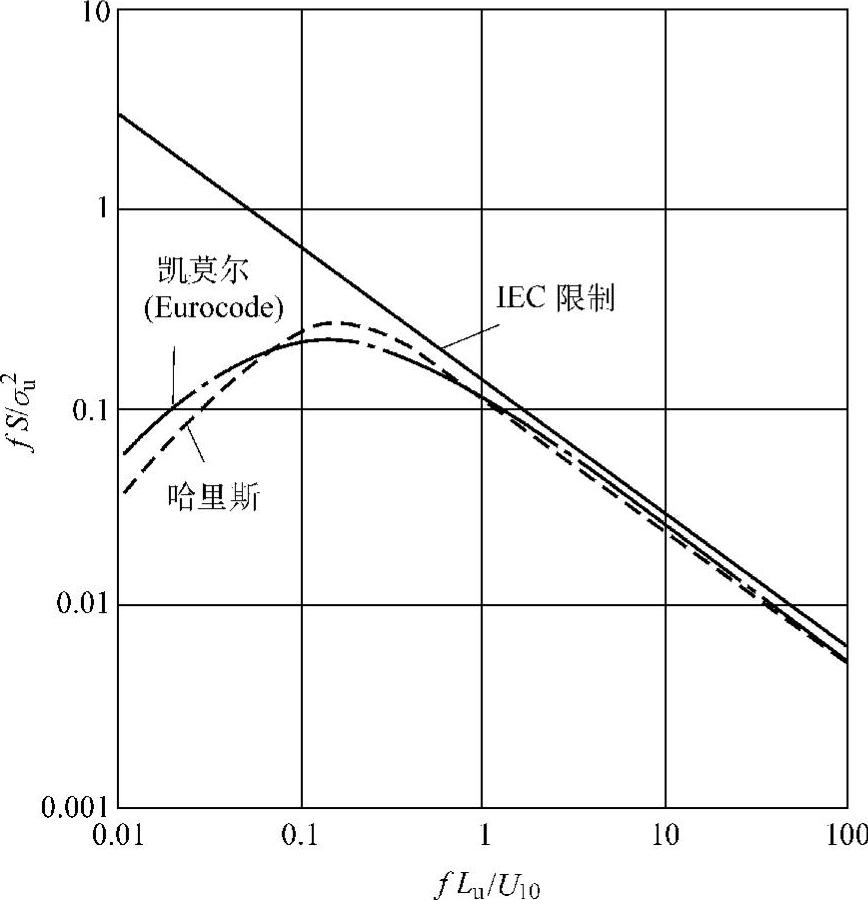
图3-5 哈里斯、凯莫尔及IEC功率谱密度的比较
一段时间内任意一点的风速都和其他点不同,两点之间的距离越近,它们风速的相关性越大。风速在空间上形成一个随机场,一个常用的描述风速场自相关函数的模型可以从下面的指数达文波特(Davenport)相干谱公式中导出:
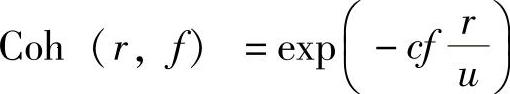
式中 r——两点之间的距离;
u——距离r之间的平均风速;
f——频率;
c——无量纲延迟常数,也被称作相干衰减,它反映风速场的相关长度。
自相关函数为
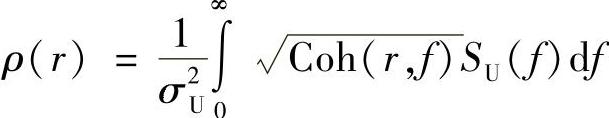
式中 SU(f)——风速的功率谱密度,这个相关模型可以考虑不同相关长度,使水平和垂直情况进一步精细化。
注意,达文波特模型的一个缺点是对r=0是不可微分的。还应注意,由于分解,极限值ρ(0)常常取稍微小于1.0的值,而达文波特模型却总是导致ρ(0)=1.0。
注意,参考上面的内容作为功率谱密度模型的一个参数,积分长度尺度Lu定义为
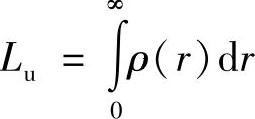
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




