航空材料检测中的分布函数和可靠度

分布函数F（x_p）也称为累积频率函数，是指随机变量X小于某一数值x_p的概率，对概率密度函数f（x）进行积分，下限取为-∞，上限取为x_p，即可得到分布函数，即

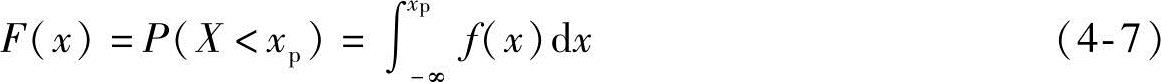
按照积分的定义，分布函数F（x_p）可用图4-2中的阴影面积表示。当x_p值增加时，阴影面积变大，F（x_p）值随之增大。可见，当已知概率密度函数f（x）时，分布函数F（x_p）[即X＜x_p的概率P（X＜x_p）]，完全取决于x_p的大小。

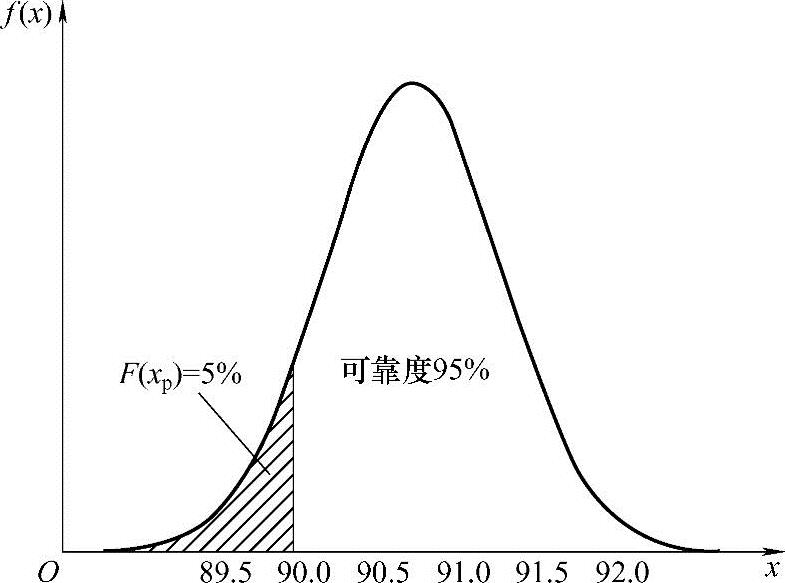
在疲劳可靠性中，分布函数以及概率密度函数占有极其重要的地位。这里简要说明它们的物理意义及其与可靠度的关系。设已知某分布的概率密度函数为f（x），当给定任一x_p值，即可知道随机变量小于x_p的概率为F（x_p）。反之，当指定任一概率，也可求得对应这一概率的x_p值。例如，指定F（x_p）=5%（见图4-3），对应的灯泡使用寿命x_p=90个月，即随机变量小于90个月的概率为5%。这就意味着：平均100个灯泡中，可能会有5个灯泡的使用寿命低于90个月。如果将这批灯泡的安全使用寿命定为90个月，则表示100个灯泡中，可能会有5个灯泡在未达到使用寿命之前，过早地发生了失效。由此可见，指定的这个概率5%相当于“破坏率”，也就相当于灯泡寿命低于90个月时的破坏率。破坏率越小，安全使用寿命就越低。对于飞机结构中的零部件，破坏率常取0.1%。它表示1000个零部件中，只能有一个零部件未达到安全寿命而提前发生破坏。这样小的概率，实际上很难实现，因此，由此破坏率确定的安全寿命是比较可靠的。对于重要的零部件，破坏率还可以取得更低一些。对于一般便于更换或易于检查的零部件，则破坏率可以取得高一些，从而给出较高的安全寿命。

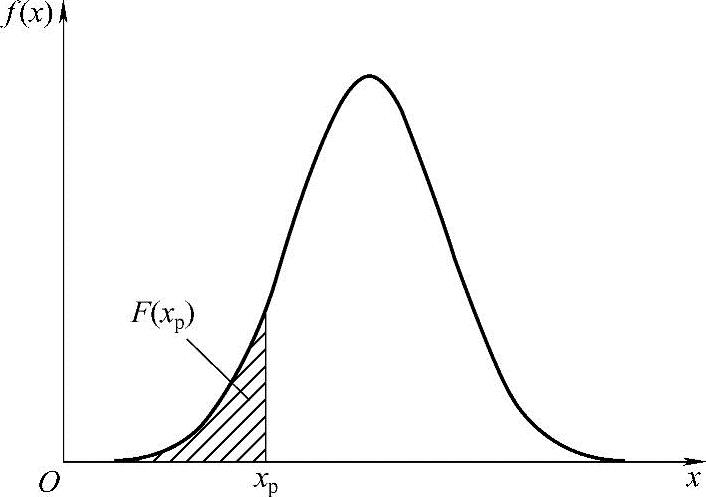
图4-2 对概率密度曲线积分得到随机变量X的分布函数F（x_p）

(www.xing528.com)

图4-3 可靠度和概率密度曲线的关系

由于概率密度曲线和横坐标轴之间所包围的面积为1，故图4-3中阴影面积右边的空白面积为95%。它表示随机变量X大于90个月的概率，即灯泡使用寿命为90个月的“存活率”。这意味着：平均100个灯泡中，可能会有95个灯泡的使用寿命都比90个月长。在疲劳可靠性中，通常将存活率称为“可靠度”。可靠度和破坏率之间存在以下关系：

破坏率+可靠度=1 （4-8）

此关系的数学形式为

P（X＜x_p）+P（X≥x_p）=1 （4-9）

当破坏率取0.1%时，可靠度为99.9%。由此可知：安全寿命的可靠性如何，可以通过可靠度显示出来。如可靠度定得较高，虽然给出较低的安全寿命，但可靠性较大。可靠度是安全寿命的“可靠性”指标。在飞机零部件的可靠性设计中，都会要求其寿命具有一定的可靠度。