摩擦自激振动解析解的争议：不确定机械问题的建模与控制补偿

如果外加主动控制力u=0，那么广义摩擦力F（v）的模型性质将决定系统式（7-4）如何产生自激振动和自激振动的形式。文献[2，3]提出负阻尼理论来解释摩擦自激振动成因，在文献[2]中假设式（7-4）中的摩擦力是如下形式

F（v）=F₀+γ·x（7-5）式中F₀——速度为零时的摩擦力；

γ——摩擦力曲线的斜率。

将方程（7-5）代入式（7-4），可得下式

上面方程的解为

x（t）=ae^-iΩt+b（7-7）

式中a和b——常数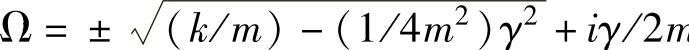；m。

另外，文献[3]进一步忽略了上面方程中F₀项，使得求解更为简化。从而用负阻尼效应解释摩擦自激振动成因及其形式。

但是，文献[1]认为这一理论存在缺陷，有可能和实验结果相违背。造成负阻尼理论和实际相矛盾的关键在于两方面：一是方程中的常数力项（如F₀）被不合理地抛弃了；二是忽略了静摩擦力与动摩擦力之间差值的影响。(www.xing528.com)

最近，文献[5]给出了另一种解释并给出了摩擦产生极限环振荡的条件，该文将摩擦力F在v₀点进行泰勒展开

式中F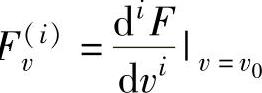，i=1，2，3。

将上面方程代入式（7-4）中，可得下式

上面方程可转化成如下方程求解

式中

v=ωt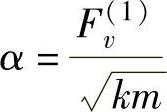

y（v）=x（v）/x₀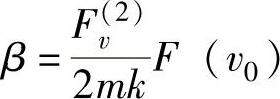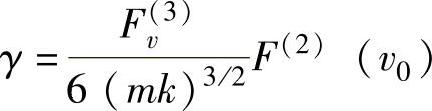通过求解上面的微分方程可获得系统的响应，并进一步给出了极限环产生的条件。

通过上面的分析可以看出，从微分方程的解析解给出的摩擦自激振动成因是在假设摩擦力满足某特定条件下进行的。这种分析有一定的理论意义，但正如文献[1]所指出的，有可能和实验结果相违背或有些偏差，原因在于摩擦力模型的假设与简化都是为了能给出解析解，忽略了实际物理意义。