离散无记忆序列信源的熵分析

假设随机序列X=（X₁，X₂，…，X_N）中的各分量之间相互独立，即X是N维离散无记忆序列信源（离散无记忆N次扩展信源），则其概率满足

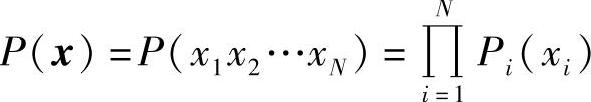
将上式代入式（2.65），可得该离散无记忆序列信源的熵为

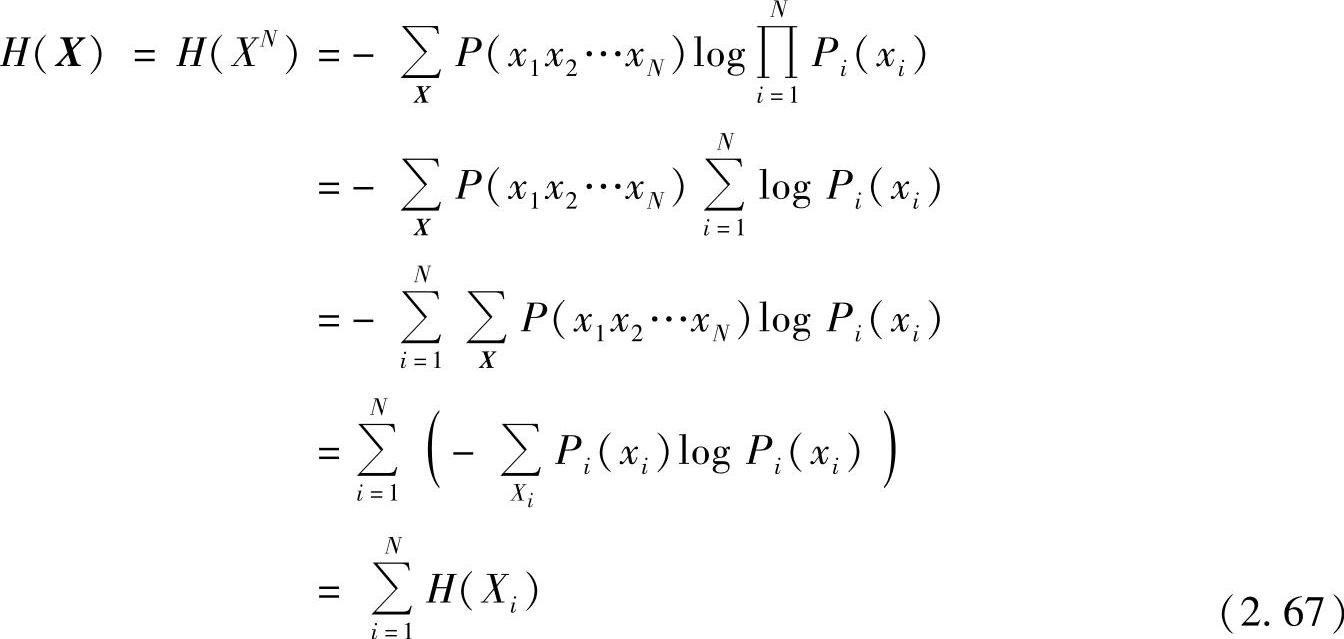
式（2.67）表明，离散无记忆序列信源的熵等于每一分量信源的熵的和。

在以上条件的基础上，进一步假设信源序列满足平稳性（是平稳的离散无记忆序列信源），即离散序列信源X的各分量的概率分布相同，则其联合概率满足

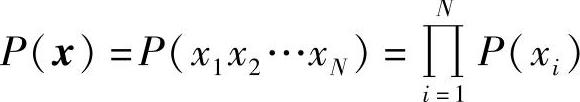
此时，各分量信源的熵相同，即H（X₁）=H（X₂）=…H（X_N）=H（X），由式（2.67）可得平稳的离散无记忆序列信源的熵为

H（X）=H（X^N）=NH（X） （2.68）

式（2.67）和式（2.68）的结论也可以根据熵的性质2.16（可加性）直接证明。

利用定义式（2.66）可以计算N维序列信源的平均符号熵H_N（X）。特别地，如果该N维序列信源是平稳的、无记忆的，则有H_N（X）=H（X）。

将上述分析结果总结为离散无记忆序列信源的熵定理如下：

定理2.1 1）离散无记忆信源X的N维序列信源X=X^N=（X₁，X₂，…，X_N）的熵H（X）=H（X^N）是信源X的各维信源熵H（X_i）（i=1，2，…，N）的和（见式（2.67））。(www.xing528.com)

2）当该信源还具有平稳特性时，N维序列信源X=X^N=（X₁，X₂，…，X_N）的熵是信源X的信息熵H（X）的N倍（见式（2.68））。

【例2.29】

求下列离散无记忆信源X的二次扩展信源及其信源熵。

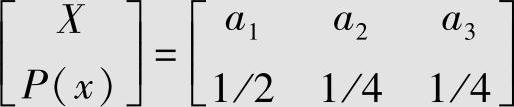
解 给定信源X的二次扩展信源X²的概率空间见表2.4。离散无记忆信源X的熵为

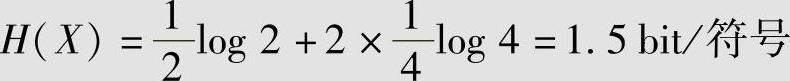
其二次扩展信源X²的熵为

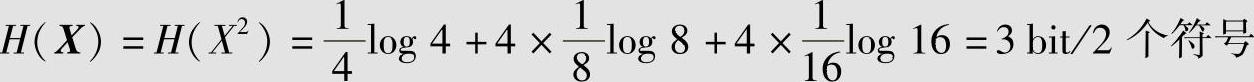
可见，H（X）=2H（X）。

表2.4 例2.29的二次扩展信源的概率