基于粒子群算法和混合罚函数法的优化求解方法

粒子群（PSO）算法通过群体之间的信息共享和个体自身经验的总结来修正个体行动策略，最终求取优化问题的解。PSO中每个优化问题的潜在解都是搜索空间中的一个“粒子”，所有粒子均有一个由优化函数决定的适应值；此外，每个粒子均有一个速度决定其飞翔的方向和距离。PSO初始化为一群随机粒子，通过迭代找到最优解。在每次迭代中，粒子本身找到的最优解，称为个体极值p_best；另一个极值是整个种群目前找到的最优解，称为全局极值g_best，每个粒子根据如下公式更新自己的速度和位置：

v_T+1=φ₀v_T+φ₁r₁（T）（p_best-x_T）+φ₂r₂（T）（g_best-x_T） （7-14）

x_T+1=x_T+v_T+1 （7-15）

式中 T———迭代次数；

x_T———第T次迭代时粒子的空间位置；

v_T———第T次迭代时粒子的速度，v^j_T≤r（x_j^max-x_j^min），v^j_T为第T次迭代时离子的第j维速度，x_j^max和x_j^min为第j维的取值范围，r为最大允许变化系数；

φ₀———惯性常数；

φ₁和φ₂———学习因子；

r₁（T）和r₂（T）———（0，1）内的随机数。

在求解有约束优化问题时，最常采用的办法是罚函数法。罚函数法的基本思想是：把一般较复杂的有约束最优化问题转化为简单的无约束问题，通过求出无约束问题的最优解来逼近原有约束最优化问题的解。罚函数法可以分为两大类：外点法和内点法，分别从可行域的外部和内部逐步趋近于约束边界的最优点。本模型求解方法采用的混合罚函数法是外点法和内点法的组合。

对于有约束最优化模型：

在构造混合罚函数时，对于等式约束h_i（x）=0用外点法构造惩罚项，对于不等式约束g_j（x）≤0用内点法构造惩罚项。添加罚函数后的增广目标函数形式为(www.xing528.com)

式（7-17）中，r^（k）为罚因子，它是一个递减的无穷序列。其中第二项是外点法的惩罚项，其作用是当r^（k）减小而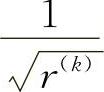增大时，迫使搜索点从被违反的不等式约束边界的外部向边界内移动，并同时靠近等式约束边界。上式第三项是内点法的惩罚项，其作用是使搜索点不越出已被满足的不等式约束边界，但随着r^（k）的不断减小，却可使搜索点向有效约束边界逼近。

通过添加罚函数，原优化问题就转化为如式（7-17）的无约束极小化问题。极小化罚函数P[X，r^（k）]，则可求得相应的极值点x[r^（k）]，当k充分大时，x[r^（k）]即为原优化模型的最优解。

设计算法时需要考虑以下几个问题：

1）初始粒子x^（0）的选取。初始粒子x^（0）必须要满足为解算问题的内点，这是因为选取了混合罚函数的缘故。若随机生成的初始粒子不为系统的内点，则必须要进行修正。修正时，在不满足约束的条件中，取一个g_k（X）（k=s+1，s+2，…m）作为临时目标函数，求在满足s不等式约束下，所有被违反的不等式约束之和的负值极小化。该极小化求解同样采用构造罚函数的方法来进行，得到满足所有不等式约束的内点。

2）在PSO算法中，p_best和g_best的更新是根据式（7-14）、式（7-15）进行的，但是在本章的算法中由于采用了混合罚函数，故需将式（7-14）、式（7-15）进行更新。

3）惯性权重系数w的确定：在PSO算法中，较小的w可以使粒子在局部空间内挖掘最优解，较大的w可以使粒子探索更大的空间，有利于发现全局的最优解，合适的惯性权重系数可使迭代过程在局部和全局寻优中达到平衡。因此为了使粒子合理地搜索解空间区域，通常用自适应改变惯性权重系数来克服PSO在迭代后期全局搜索能力的不足的缺点：

式中 iter_max———最大的迭代次数；

iter———当前的迭代次数。

该式表示在迭代初期采用较大的w值以加快全局搜索，随后将w逐代减小，以获得更为精细的结果。

4）r^（0）的选取以及罚因子缩小或增大的规律，对无约束极小化的次数，甚至对罚函数法的成败，都有着极大的影响。用内点法时，r^（0）过大，或用外点法时，r^（0）过小，罚函数容易极小化，但其极小点离约束最优解较远，使极小化次数增多；反之，罚函数极小点离约束最优解较近，但又可能在初次极小化时遇到困难。经过实验，我们将初始罚因子设为1，并且令r^（k）=cr^（k-1），其中c为0.5，这样来保证r^（k）是一个无穷递减序列。