三种典型信号的稳态误差分析

《控制系统MATLAB计算及仿真》已对三种典型给定输入信号作用下的稳态误差进行了充分复习。需要特别强调，定义系统误差e（t）=r（t）-b（t），只有当H（s）=1时，e（t）=r（t）-c（t），《控制系统MATLAB计算及仿真》中的相关公式才适用。还要强调单位加速信号是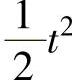。在解算有关加速信号的题目时，要特别关注t²前的系数。

【例7-5】 对图7-4所示系统：1）当K=8、a=0时，确定系统的阻尼比ζ、无阻尼自然振荡角频率ω_n与在r（t）=t作用下系统的稳态误差e_ss；2）当K=8、ζ=0.7时，确定参数a与在r（t）=t作用下系统的稳态误差e_ss；3）在保证ζ=0.7与在r（t）=t作用时e_ss=0.25的条件下，确定参数a与K。

解：1）当K=8、a=0时，确定ζ、ω_n与e_ss。

①当a=0时，求Φ（s）。

clear；syms s G H a zeta omegan；G=8/（s∗（s+2））；a=0；H=1；

[n，d]=numden（G/（1+G∗H））；phi=simple（n/d），

程序运行后得到。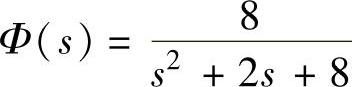

②求ζ、ω_n。

clear；syms s zeta omegan；

[zeta，omegan]=solve（omegan^2=8，2∗zeta∗omegan=2）；

zeta=vpa（zeta，4），omegan=vpa（omegan，4），

程序运行后得到ζ=0.3535、ω_n=2.828。

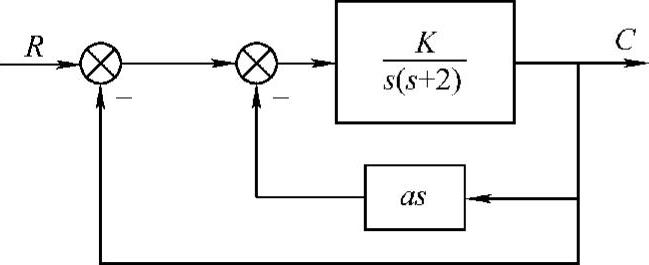
图7-4 双闭环系统

③对系统判稳。

clear；P=[128]；roots（P），

程序运行结果是系统的特征根均有负实部，根据代数稳定判据，系统稳定。

④求e_ss。

在r（t）作用下，闭环系统误差（象函数）。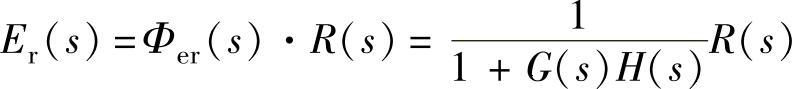

clear；syms s；G=8/（s∗（s+2））；H=1；xb=1；r0=0；v0=1；

a0=0；[essrr0，essrv0，essra0]=insteerr（G，H，xb，[r0，v0，a0]）；

程序运行后得到e_ssv=1/4。

2）当K=8、ζ=0.7时，确定参数a与在r（t）=t作用下系统的稳态误差e_ss。

①当ζ=0.7时（a≠0），求Φ（s）。

clear；syms a G H1 H phi1 phi s；G=8/（s∗（s+2））；H1=a∗s；H=1；

phi1=simple（G/（1+G∗H1）），phi=simple（phi1/（1+phi1∗H）），

程序运行后得到、。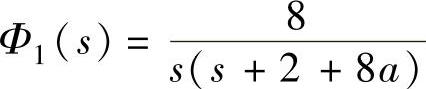

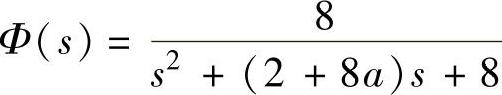②求a、ω_n。

clear；syms a s zeta omegan；zeta=0.7；

[a，omegan]=solve（omegan^2=8，2∗0.7∗omegan=2+8∗a）；

a=vpa（a，4），omegan=vpa（omegan，4），

程序运行后得到a=0.245、ω_n=2.828。

③对系统判稳。

clear；a=0.245；P=[12+8∗a 8]；roots（P），

程序运行后得知系统的特征根均有负实部，根据代数稳定判据，系统稳定。

④求e_ss。

clear；syms s；G=8/（s∗（s+2+8∗0.245））；H=1；xb=1；r0=0；v0=1；a0=0；

[essrr，essrv，essra]=insteerr（G，H，xb，[r0，v0，a0]）；essrv=vpa（essrv，4），

程序运行后得到e_ssrv=0.495。

3）在保证ζ=0.7与在r（t）=t作用时e_ss=0.25的条件下，确定参数a与K。

①求e_ss的数学表达式。

clear；syms a K G H1 H phi1 phi s；G=K/（s∗（s+2））；H1=a∗s；H=1；R=1/s^2；

phi1=simple（G/（1+G∗H1））；Er=simple（R/（1+phi1∗H））；essr=limit（s∗Er，s，0，right），

程序运行结果essr=（2+K∗a）/K。

②求参数a与K。

clear；syms a K omegan；

[K，a，omegan]=solve（（2+a∗K）/K=0.25，1.4∗omegan=2+a∗K，omegan^2=K）；

K=vpa（K，4），a=vpa（a，4），

程序运行后得到K=31.36，a=0.1862。

4）验证确定参数a与K后，在r（t）=t作用下的稳态误差e_ss=0.25。

①求局部反馈内环传递函数。

clear；syms a K G H1 H phi1 phi s；G=31.36/（s∗（s+2））；(https://www.xing528.com)

H1=0.1862∗s；phi1=simple（G/（1+G∗H1）），

程序运行结果phi1=490000/（15625∗s+122488）/s。

②验证确定参数a与K后e_ss=0.25。

clear；syms s；G=490000/（15625∗s+122488）/s；H=1；xb=1；r0=0；v0=1；a0=0；

[essrr，essrv，essra]=insteerr（G，H，xb，[r0，v0，a0]）；essrv=vpa（essrv，4），

程序运行后得到e_ssrv0=0.25，说明以上参数计算正确。

需要说明的是，多元联立方程求解时，按未知变量的英语字母顺序列出其解，先列大写字母的，后列小写字母的。故等号左端方括号内需按此规则顺序输入未知变量。有困难时，可验算其根来解决。

【例7-6】 对图7-5所示系统，指定e（t）=r（t）-c（t）。1）当K₂=1时，试问系统对r（t）是几型的？2）若使系统对r（t）为Ⅰ型的，试计算选择K₂的值。

解：1）当K₂=1时，容易看出系统对r（t）是0型的。

2）求系统闭环传递函数。

clear；syms K1 K2 T1 T2 s R C B E G H1 G1phi；

G=K1/（（T1∗s+1）∗（T2∗s+1））；H=K2；

phi=factor（G/（1+G∗H）），

程序运行结果phi=K1/（T1∗s^2∗T2+T1∗s+T2∗s+1+K1∗K2）。

求等效单位反馈系统的前向通道传递函数。

clear；syms K1 K2 T1 T2 s R C B E G H1 G1phi；

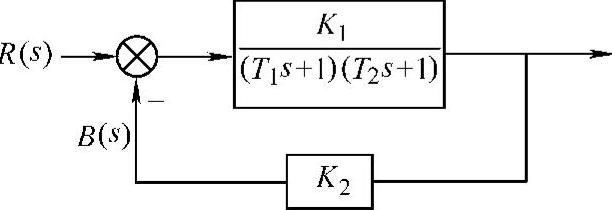
图7-5 负反馈控制系统

[G]=solve（K1∗（1+G）=G∗（T1∗s^2∗T2+T1∗s+T2∗s+1+K1∗K2），G）；

G=factor（G）；G=collect（G，s），

程序运行结果G=K1/（T1∗s^2∗T2+（T1+T2）∗s-K1+K1∗K2+1）。

分析前向通道传递函数表达式，当系统为Ⅰ型系统时，其G（s）应有一个积分环节，那么，表达式分母的一部分值K₁K₂-K₁+1应为0。

计算选择K₂的值。

clear；syms K1 K2；[K2]=solve（（1+K1∗K2-K1）=0，[K2]），

程序运行后得到。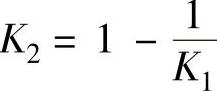

【例7-7】 设复合控制系统框图如图7-6a所示。已知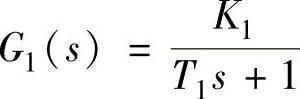、、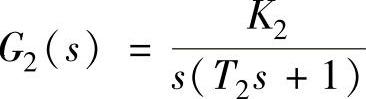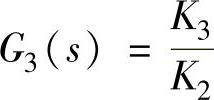。系统在扰动输入n（t）=1（t）作用下，要求系统稳态误差为零，试确定顺馈通道

的传递函数参数G_n（s）。

解：1）将控制系统框图7-6a等效变换，如图7-6b所示。

2）关系式。根据自动控制原理，对系统等效结构图有以下关系式，即

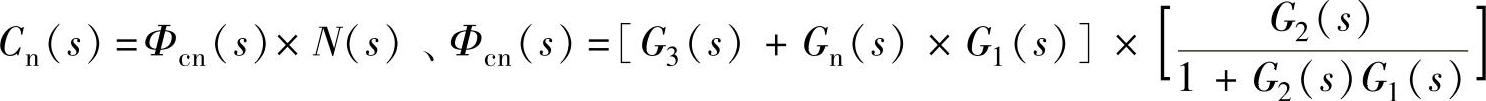
还有e（t）=r（t）-c（t），当r（t）=0时，e_n（t）=-c_n（t）或E_n（s）=-C_n（s）。

3）计算系统的E_n（s）。

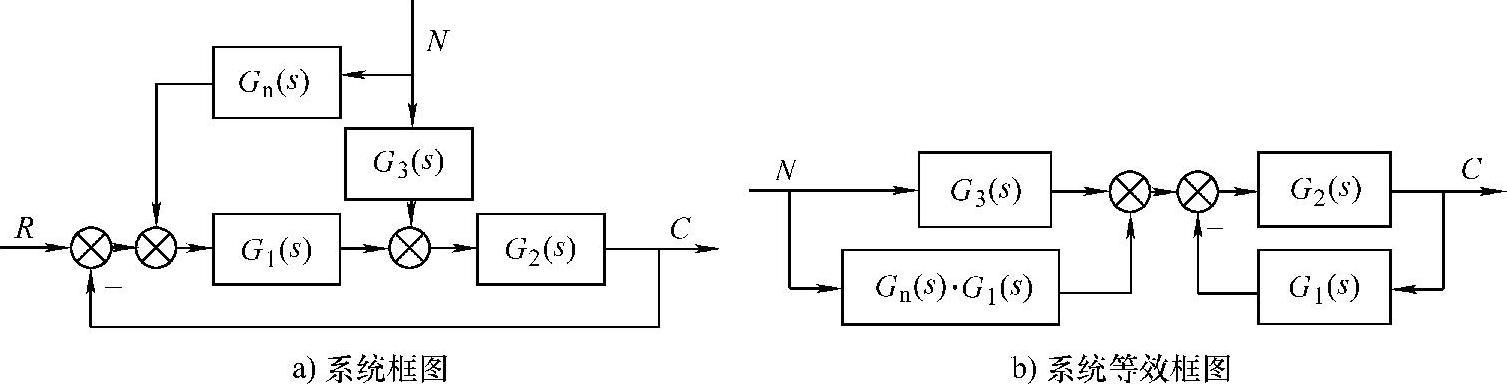
图7-6 复合控制系统

clear；syms s G1 G2 G3 Gn K1 K2 K3 T1 T2 N n　phien Cn En；

G1=K1/（T1∗s+1）；G2=K2/（s∗（T2∗s+1））；G3=K3/K2；

phien=（G3+Gn∗G1）∗（G2/（1+G2∗G1））；

n=sym（1（t））；N=laplace（n）；Cn=phien∗N；En=factor（-Cn），

程序运行结果

En=-1/s∗（K3∗T1∗s+K3+Gn∗K1∗K2）/（T2∗s^3∗T1+T2∗s^2+T1∗s^2+s+K1∗K2）

4）分析关系E_n（s）的表达式。

只要E_n（s）表达式分子为0，在扰动输入n（t）=1（t）作用下，系统稳态误差就能为零。也就是当K₃T₁s+K₃+G_nK₁K₂=0时，e_ss=l_s→im₀s·E（s）=0。

clear；syms s K1 K2 T1 T2 En ess；

En=-1/s∗0/（T2∗s^3∗T1+T2∗s^2+T1∗s^2+s+K1∗K2）；

ess=limit（s∗En，s，0，right），

程序运行结果ess=0。

5）计算顺馈通道的传递函数参数G_n（s）。

clear；syms Gn s K1 K2 K3 T1 T2 Gn；

[Gn]=solve（K3∗T1∗s+K3+Gn∗K1∗K2=0，Gn），

程序运行后得到G_n（s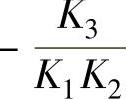）=（T₁s+1）。