地下水数值模拟基础：系数矩阵存储方式讨论

有限元法形成的系数矩阵(渗透矩阵)[A]有下列特点:

1.高度稀疏性

从组成矩阵[A]的元素:

来看,由于基函数的特点,ψi只在共有结点i的几个单元上不为0,其他单元上均为0;ψj也只在共有结点j的几个单元上不为0,其他单元上均为0,所以d i,j和p i,j就只有在共有结点i和j的极少数几个单元上(也即共有结点i的几个单元和共有结点j的几个单元中能彼此重叠的几个单元)不为零,其余大量单元上都是0。因此矩阵[A]是高度稀疏的,非零元素的个数和矩阵的阶数相比,一般不超过10%,矩阵的阶数大时,一般不超过5%。

2.对称性

即使各向异性介质,渗透系数或导水系数也是对称张量,从d i,j和p i,j的特征可以看出所形成的矩阵是对称的。所以只要存贮一半,另一半元素可以利用对称性求得。

3.非零元素分布的规则性

只要结点编号方法选择得合理,d i,j和p i,j的上述特征决定了这些非零元素在矩阵[A]中位于主对角线的两侧,呈带状分布。

鉴于系数矩阵的高度稀疏性,如果不加任何处理,就要对那些0进行无效运算,为此有必要把这些零元素从存贮中去掉,以加快运算速度。现在介绍一种能有效节省存贮量的存贮方法-变带宽一维存贮法。为此先介绍带宽的概念。所谓带宽是指在每行中,一般地说从第一个非零元素起,到对角线元素为止的元素的个数(实际上只包括了大约一半元素,并不是这一行的全部非零元素,故实为半带宽)。设第i行的带宽为nn[i],则

式中:n为该矩阵的阶(方程的个数)。

矩阵[A]各行带宽的总和(即总带宽)为mR=nn[i],此时,如果元素a i,j(j≤i)作为一维数组G[1∶mR]的元素而言,则是第nn[p]-(i-j)个元素。既然元素按带状分布,假如我们只对带状区域内的元素进行编号,摒弃带外的零元素,在计算过程中可以大大节省总存贮量。这就要求带外的零元素在计算过程中始终保持为零,或者说在计算过程中保持[A]的带状和带宽。

采用一维数组G[1∶mR]进行存贮,此时整个[A]只存贮它的下三角形部分(包括对角线元素)的元素,按行的次序一行接一行地排成一维数组存入计算机中。对每一行来说,事实上只存贮它最左边第一个非零元素起,到对角线元素为止的所有元素(包括带内的零元素)。逐行累加依次对各元素进行编号,并用下标变量M[i]表示第i行最后一个元素(即对角线元素a i,i)的编号。为方便起见,通常规定M[0]=0。由M[i]的含义可知,第i行元素共有nn[i]个。这些元素的编号依次为

M[i-1]+1、M[i-1]+2、…、M[i-1]+nn[i]=M[i]

为了便于理解,下面通过一个六阶带状对称正定矩阵[A]的例子来具体了解上述编号规则。编号规则如下:

每个元素a i,j右上角括弧内的数字就是按一维数组存贮时相应的编号,一共有12个元素。用一维数组G[1∶12]来存贮这些编号元素,即G[1]、G[2]、…、G[12]中存放的元素分别为a 11、a 21、a 22、…、a 66。此外,还要用一个一维辅助数组M[1∶6]来存放对角线元素的编号,即M[1]=1、M[2]=3、M[3]=6、M[4]=7、M[5]=9、M[6]=12。

每行的带宽(www.xing528.com)

nn[i]=M[i]-M[i-1] (i=1,2,…,6)

即nn[1]=1,nn[2]=2,nn[3]=3,nn[4]=1,nn[5]=2,nn[6]=3。这样带状区域内输入计算机的每一个元素对应于一个编号;反之,每一个编号也对应于一个元素。带状区域以外的零元素不予存贮。

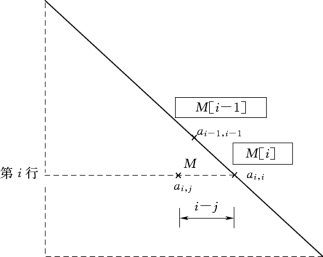
图3-6　元素编号m与其下标

下一步还必须知道在一维数组中编号为m的元素位于矩阵[A]中哪一行哪一列,即如何求得[A]中i行j列元素的编号。为此需要讨论一维元素编号m和下标i、j之间的关系。设a i,j是带状区域内需要输入计算机的一个元素,其编号为m。由于a i,j位于i行,所以有

如果i≠j,则a i,j必位于a i,i的左边。a i,j至a i,i之间还有i-j个元素(图3-6),即

或

此式表明编号为m的元素位于哪一列,即

利用式(3-32)和式(3-34)可知G中编号i、j的关系为m的元素位于哪一行哪一列。反之,由式(3-33)可知[A]中第i行j列元素在G中的编号。因为由i就可以知道M[i]的数值。知道了M[i]、i、j以后,式(3-33)会提供编号m的值。由于i行第一个非零元素的编号为M[i-1]+1,所以由式(3-34)还可以知道它必位于第i-M[i]+M[i-1]+1列。

由式(3-32)、式(3-33)得

上式可用来判别任一元素a i,j是否编了号。若i、j满足式(3-35)表示对a i,j已经编了号。

现以上述六阶矩阵为例来说明m、i、j之间的转换。如已知a i,j的一维数组编号m为4,i、j是多少?m必须满足式(3-32),今m=4,位于M[2]=3,M[3]=6之间,故i=3。再由式(3-34)得j=1。即编号为4的元素为a 3,1。

已知a 5,4,它在一维数组中的编号是多少?由式(3-33)得m=8。

第4行第一个非零元素位于哪一列?由j=i-M[i]+M[i-1]+1知j=4。