非均匀平面薄片质量计算

设有一平面薄片在xOy面上占有闭区域D，它在点（x，y）处的面密度函数为ρ（x，y），其中ρ（x，y）＞0且在D上连续，现在要计算该薄片的质量M.当面密度ρ（x，y）为常数时，此时的薄片是均匀的.其质量可用公式

来计算.但现在面密度ρ（x，y）是变化的，因此，薄片的质量不能直接用上述公式来计算，可采用引例1的思路和方法来解决.

（1）大化小.用任意的曲线网把闭区域D分成n个小闭区域

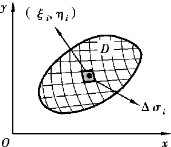
图9-3

Δσi（i=1，2，…，n）同时表示对应小区域的面积（见图9-3）.Δσi对应的质量记为ΔMi，显然

（2）常代变.在每个小区域Δσi中任取一点（ξi，ηi），因为ρ（x，y）在D上连续，所以当区域Δσi很小时，密度ρ（x，y）在Δσi上的变化也很小（见图9-3）.这时，小块薄片可近似地看成均匀薄片，Δσi所对应的平面小薄片的密度近似等于ρ（ξi，ηi），从而Δσi所对应的平面小薄片的质量为

（3）求和.将这n个平面小薄片相加，即得整个平面薄片的质量为

（4）取极限.记λ为n个小闭区域Δσi的直径的最大值，λ越小表示区域D分割越细.当λ→0时，上述和式的极限就是所求的平面薄片的质量M，即

以上两个引例虽然实际意义不同，但解决问题的方法完全相同，并且结果都归结为同一形式的和式的极限.在力学、几何和工程技术中，有许多物理量或几何量都可归结为这一形式的和式的极限.因此，抛开上述两个实例的具体意义，便可抽象出二重积分的概念.

　定义1　设函数f（x，y）是有界闭区域D上的有界函数.用任意的曲线网将闭区域D分成n个小闭区域

其中，Δσi表示第i个小闭区域，也表示它的面积.在每个Δσi上任取一点（ξi，ηi），作乘积(www.xing528.com)

并作和

其中，f（x，y）称为被积函数，f（x，y）dσ称为被积表达式，dσ称为面积元素，x和y称为积分变量，D称为积分区域，称为积分和.

根据二重积分的定义，引例1中曲顶柱体的体积是曲顶柱体的变高f（x，y）在底D上的二重积分

引例2中，非均匀平面薄片的质量是它的面密度ρ（x，y）在薄片所占闭区域D上的二重积分

二重积分是一个和式的极限，我们自然会问，哪些函数是可积的？现有以下结论：

如果函数f（x，y）在有界闭区域D上连续，则f（x，y）在区域D上可积.

总假定函数f（x，y）在闭区域D上连续，所以f（x，y）在D上的二重积分都是存在的，后面就不再加以说明.

图9-4

在二重积分的定义中，对闭区域D的划分是任意的.于是，可选取某种特定的划分方式来计算二重积分.例如，在直角坐标系中，用平行于x轴和y轴的直线网来划分D（见图9-4），那么除了包含边界点的一些小闭区域外，其余的小闭区域都是矩形区域.设矩形区域Δσi的边长为Δxj和Δyk，则Δσi=Δxj·Δyk.因此，在直角坐标系中，面积元素dσ可记作dxdy，从而把二重积分记作

其中，dxdy称为直角坐标系中的面积元素.