连续系统的混沌现象：理论神经信息学初探

上面所说的是迭代系统，或称离散系统。下面讨论连续系统。

2.6.6.1　同宿轨道与异宿轨道［9］

设一非线性自治系统

也可写为

此方程相图如图2．56所示，C 和C′是闭轨。

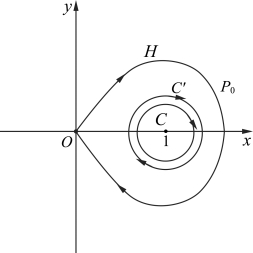
图2.56　方程（2-76）相图

H 被称为同宿轨道，O 点是同宿点（homoclinic point）。什么是同宿点？就是当时间趋向于+∞和-∞时轨道H 趋向于同一点，这一点就是同宿点，而轨道H 就称为同宿轨道。同宿轨道联系着“孤立子”。这是十分有意思的概念。

当没有外力作用时，摆的运动方程是

方程（2-77）相平面图如图2．57所示。

图2.57　异宿轨道

图2．57中有三个平衡点：中心点（0，0），两个鞍点（-π，0）和（π，0）。其中H 轨道就是异宿轨道（heteroclinic orbit），与同宿轨道相似，异宿轨道对应着“激波”。

2.6.6.2　非自治系统

当方程（2-76）中加入一些扰动信号时，其成为非自治系统

时，此时相图2．56变化如图2．58所示。同宿点也可理解为稳定流形和不稳定流形相交的点。在图2．58中可以看出，O 点附近稳定流形和非稳定流形无限皱褶。

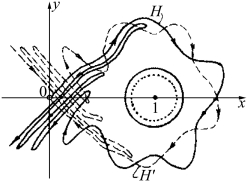
图2.58　方程（2-78）相图（图中实线是不稳定流形，虚线是稳定流形）

在图2．58中有无限个同宿点，而不稳定流形基本上就是奇怪吸引子。在吸引子中有无穷多个同宿点。系统轨道随时间延长不断接近同宿点，同时又不断离开同宿点，这就是连续系统的混沌现象。它具有与离散系统同样的混沌特性。

同样，异宿轨道加上外扰，系统如图2．59（b）所示，它对单摆系统做了一些改进，把原来不动的摆端点改为可以上下运动的，这种上下运动可以将外界输入作为干扰，它的无量纲化后方程是

该系统的相图就如图2．59（a）所示。

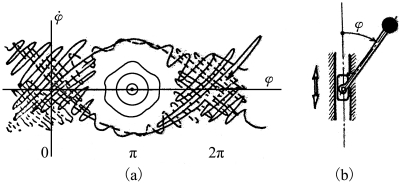
图2.59　异宿轨道加外扰

非自治系统是如何进入混沌态的？这里用一个例子进行实际计算，从参量变化中可以看出它的过程。设有一系统

当δ=0，f=0 时，系统有如图2．60所示的轨道。

图2.60　输入为0 时的相图

当δ=0．25，f=0，ω=1 时，系统轨道形状如图2．61所示。

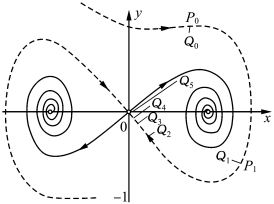
图2.61　系统参数变化时的相图(www.xing528.com)

当δ=0．25，f=0．1，ω=1 时，轨道形状如图2．62所示。

图2.62　参数进一步变化，相图变化

当δ=0．25，f=0．3，ω=1 时，轨道形状如图2．63所示。

图2.63　稳定流形与不稳定流形相交

在图2．60中，稳定流形与不稳定流形没有相交。图2．61是参数变化时的相图，但是稳定流形和不稳定流形并未相交。如图2．62所示，随着参数变化，稳定流形和不稳定流形逐渐接近（见图中S 处）。到图2．63，稳定流形与不稳定流行相交，于是出现无穷个交点（图中没有表示出来，主要为了便于我们观察），除了几个稳定点，最重要的是出现了奇怪吸引子，如图2．64所示。这个奇怪吸引子基本上是从不稳定流形发展而成的。

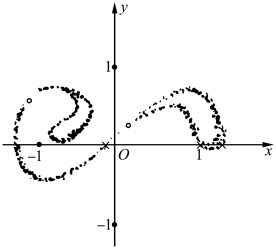
图2.64　奇怪吸引子

。—稳定不动点；“×”—不稳定不动点

当δ=0．15，f=0．3，ω=1 时，形状如图2．65所示。其中A 点是稳定不动点，它对应于一个大的周期解。

图2.65　奇怪吸引子加上一个周期解参数后继续变化的图形

这一过程实际上也就是验证梅尔尼科夫的方法表征系统混沌产生的过程［10］。

2.6.6.3　马蹄映射［9-10］

设有一区域R（ABCD）（见图2．66），它的马蹄映射过程如下：首先把R（ABCD）区拉长，图中指过程①，接着是过程②，把它对折，成为fR，然后放到原来R 方块区。R 与fR 有不相连的两个区域1．和0．，这也可表示为原来R 区域上的两个区．1 和．0 两个区。把这两者的交集是0.0，0.1，1.0，1.1 四个区（见图2．66），这就是一次马蹄变换。再同样映射一次，得到结果如图2．67所示。

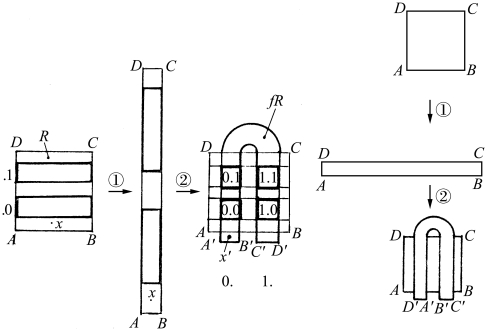
图2.66　马蹄映射

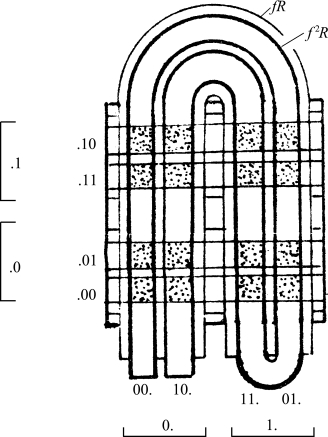
图2.67　两次马蹄映射

从黑块的变换中我们可看出（见图2．68）：

1．10→11．0

这是一种移位变换。在符号动力学中，移位变换是十分重要的特性。

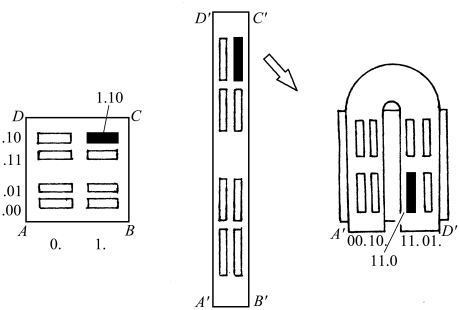
图2.68　马蹄映射对应区域

两次马蹄映射可得16 块，只要映射次数足够多，这里有由任意个0 和1组成的二进制的编号数块。数…11111．11111…或…00000．00000．…移位变换后就是原来的数，这就是周期点，如果是．…010101010．10101010101…，这样每移动两步就会相同，这就是周期2 点，同样我们可以得到无穷多周期点。

马蹄映射是研究混沌轨道有力的工具。

马蹄映射为什么重要？从数学上讲，找到了马蹄映射，就可以证明这一系统是混沌系统，作为具有混沌特性的判据。我们认为更重要的一点是，找到了马蹄映射，就找到了单调性变化的两边。图2．67实际上表明了马蹄映射的符号动力学性质，表明单调性变化规律，也给出了轨道排序规律。这对混沌定量化研究而言十分重要。这里再一次说明，混沌系统轨道并不杂乱无章，或者说混沌轨道并不“混沌”。图2．67那样的变换又被称面包师变换（baker’s transformation）。

2.6.6.4　弹跳球的马蹄变换

弹跳球运动实际上也可找到马蹄变换（见图2．69）。ABCD 这一区域可以变为A′B′C′D′。两者的交集类似于图2．66。

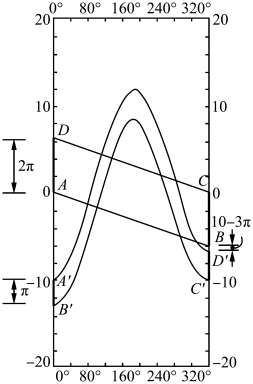
图2.69　弹跳球的马蹄映射

存在这样的映射，说明弹跳球运动存在混沌态。

看来似乎混沌现象的主要特点应归结为“乱”，归结为不规则或随机状，从有序到无序，否则也不会把它称为“混沌”。其实混沌的最核心特性是不稳定性、初值敏感性和轨道的不确定性。很显然，神经系统已经把这一特性运用到了极致，这在以后几章中可以看出。