隐马尔可夫算法实现中的基本问题

1.初始模型的选取

根据Baum-Welch算法，由训练数据得到HMM参数时，如重估式（7-120）、式（7-121）和式（7-122）所示，一个重要问题就是初始模型的选取。不同的初始模型将产生不同的训练结果。因为算法是使P（O|λ）局部极大时得到的模型参数，因此选取好的初始模型使最后求出的局部极大与全局最大接近，是很有意义的。

但是，至今这个问题仍没有完美的答案。实际处理时都是采用一些经验方法。一般认为，参数π和A的初值选取对训练出的HHM影响不大，可以随机选取或均匀取值，只要满足式（7-87）和式（7-88）中要求的约束条件即可。但参数B的初值选取对训练出的HMM影响较大，一般倾向采取较为复杂的初值选取方法。基于这种考虑，一种典型的HMM参数估计过程如图7-15所示。

这里，初始模型λ可以任意选取。但因为有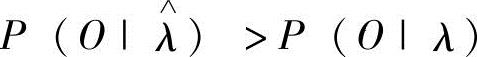，所以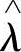是λ改进后的模型。再将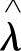作为初始值用重估公式，得到λ-。这样就避免了初值的选择不当，变经典的为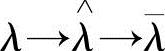。当然，沿图中虚线，不用重估公式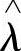，也可近似作为模型参数。

当然，从以后的讨论会看到，HMM有很多类型。因此，针对不同形式的HMM，也可采取不同的有效的初值选取方法。

2.多个观察值序列训练

实际中，训练一个HMM，经常是用到不止一个观察值序列，那么对于L个观察值序列训练HMM时，要对Baum-Welch算法的重估式（7-120）、式（7-121）和式（7-122）加以修正。设L个观察值序列为O^（l），l=1，…，L，其中O^（l）=O₁^（l），O₂^（l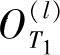），…，，假定各个观察值序列独立，此时有

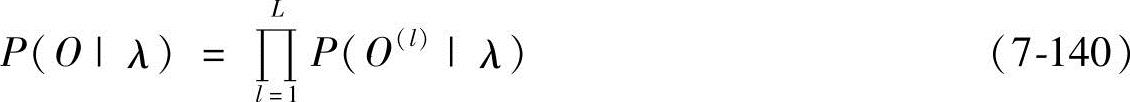
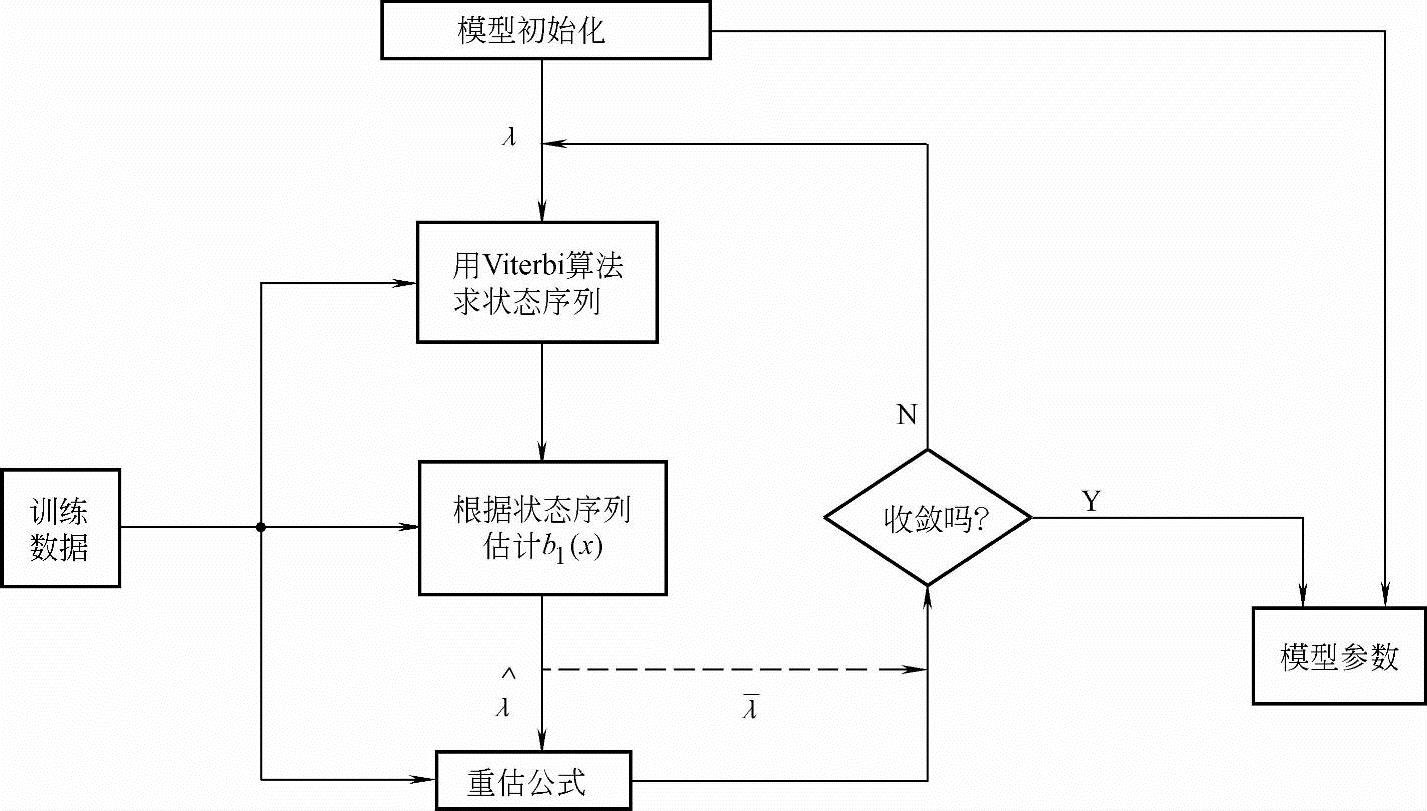
图7-15 一种HMM参数估计方法示意图

由于重估公式是以不同事件的频率为基础的，因此，对L个训练序列，重估公式修正为

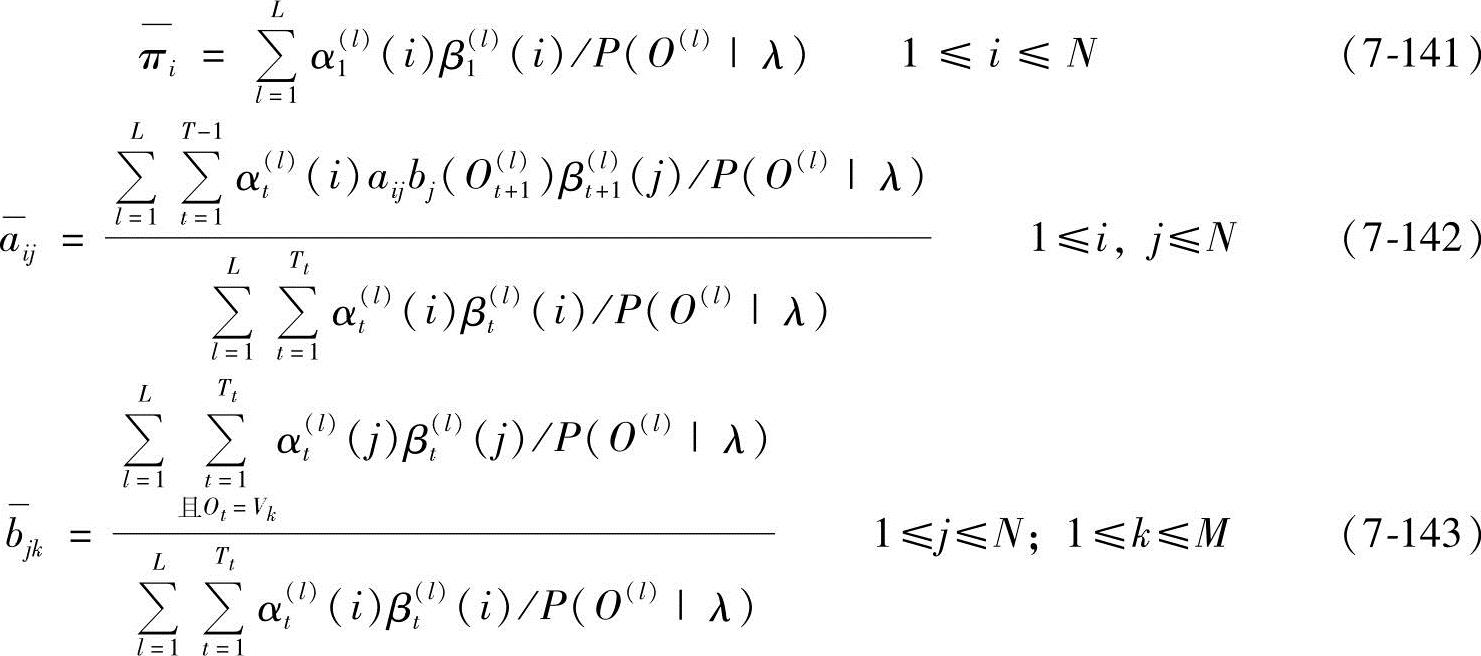
3.比例因子问题

在前向-后向算法和Baum-Welch算法中，都有α_t（i）和β_t（i）的递归计算，因为所有量都小于1，因此α_t（i）（随着t的增加）和β_t（i）（随着t的减少）都迅速趋向于零，为了解决这种下溢（Underflow）问题，必须采取增加比例因子（Scaling）的方法，对有关算法加以修正，处理过程为

（1）对α的处理

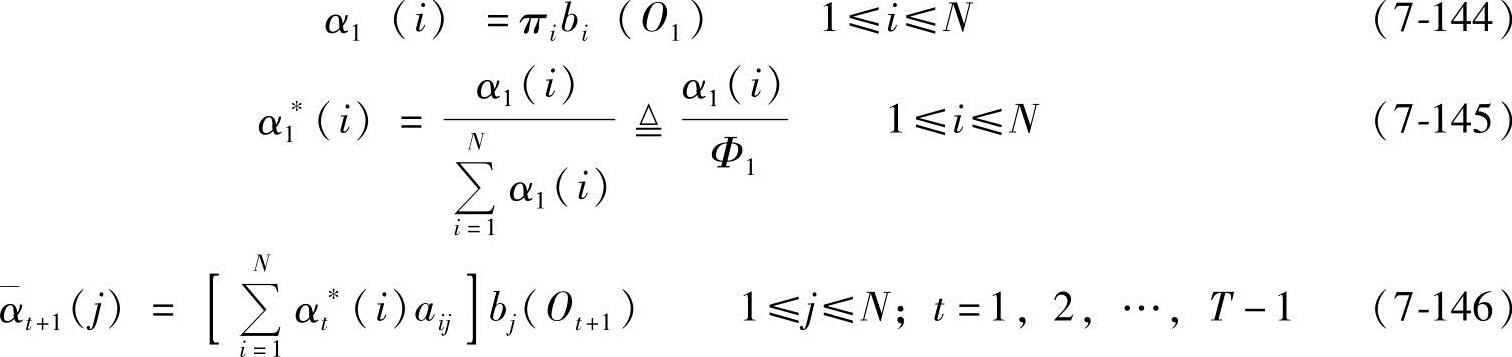
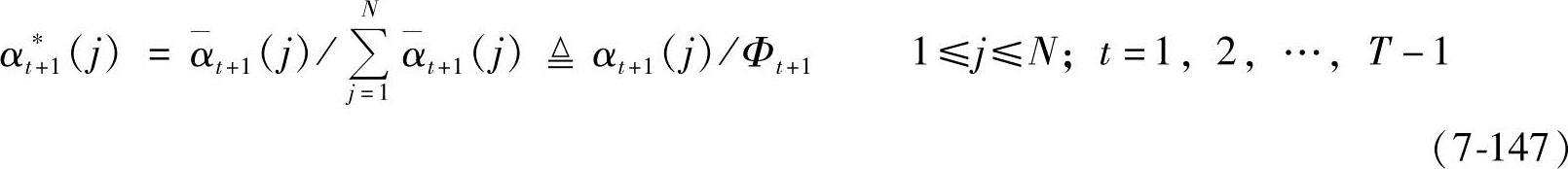
（2）对β的处理

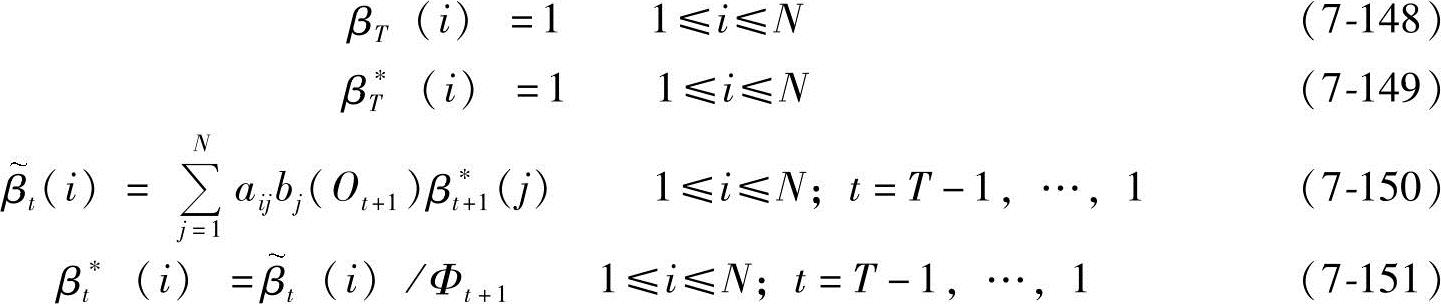(www.xing528.com)

（3）常用计算公式的处理 对α和β做了上述处理之后，为了保持原有公式计算的结果不变，必须在常用计算公式中做相应处理，以消去比例因子的影响。

1）概率P（O|λ）的计算公式：由α的处理过程易推出

α_t^*（i）=a_t（i）/（Φ₁Φ₂…Φ_t） （7-152）

而

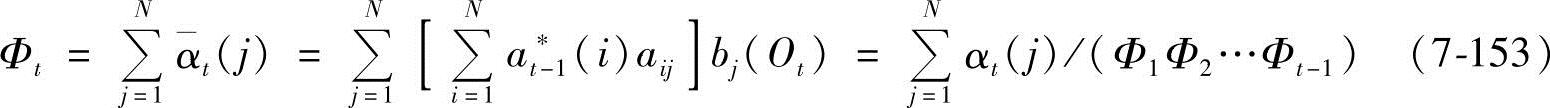
因此

即

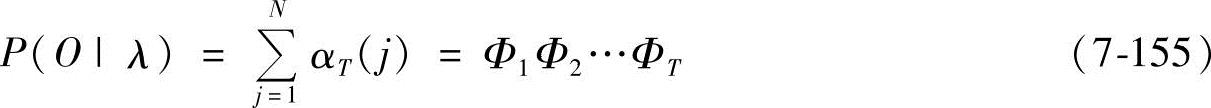
或

2）重估公式：由β的处理易知

因此，重估（多个训练序列）时，式（7-120）、式（7-121）和式（7-122）变为

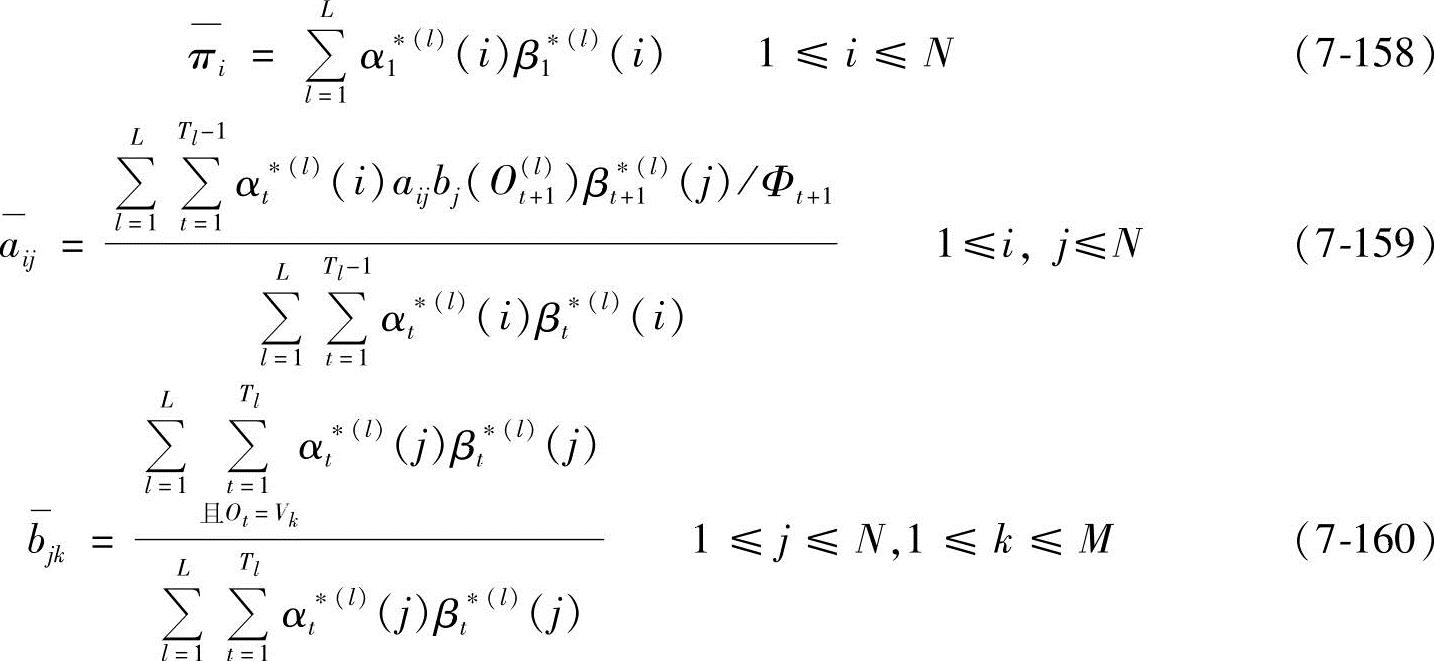
4.HMM的其他形式

在上面几节中所讨论的HMM，由于其观察值是M个离散可数的观察值中的一个，因而称之为离散的HMM，某个状态j所对应的观察值的统计特性是由一组概率b_jk（k=1，2，…，M）来描述的。除了这种经典离散HMM以外，HMM还有其他各具特色的形式，由于经典离散HMM主要由图7-13所示的两部分组成，而其他形式的HMM都是从这两部分出发，对这两部分进行不同的修正而产生的。例如，如果修正图7-13所描述的第二部分由B描述的随机过程，可以得到连续的和半连续的HMM。所谓连续HMM，是指观察值为一个连续随机变量X，因此，某一个状态j对应的观察值统计特性由一个观察值概率密度函数b_j（X）表示；而半连续HMM可以认为是HMM的一种一般形式，连续HMM和离散HMM都是其特例。而且，半连续HMM在一定程度上兼有两者的长处。因为HMM对连续向量使用离散HMM，信息丢失较大，但是如果使用连续HMM，需要使用较多的概率密度函数进行混合，模型复杂，运算量大，并且需要使用更多的训练数据才能得到可靠的模型。如果对图7-13所示的第一部分，也就是由π、A描述的马尔可夫链加以修正，就可以得到另外三种主要的HMM，即利用Gibbs分布取代马尔可夫链的HMM；在马尔可夫链中加入状态驻留时间参数的HMM，以及二阶HMM。此外，还有其他一些形式的HMM存在于各个应用领域，在此不再赘述。