在对2-D裁片中的各质点进行了受力分析后,还需要对模型进行运动求解。根据牛顿第二定律a=F/m,计算出质点Ui的加速度ai,然后列出偏微分方程,利用各种数值方法来求得质点在各时刻的位置与速度。
对质点经过受力分析后,方程(4-1)可展开为:
![]()
整个模型系统形式化为一个线性微分方程,方程右边除了重力Fgravity与质点位置X无关以外,其他都是X的函数,因此必须使用数值方法来进行求解。
适用于织物模拟的数值解法主要有两大类:显式积分法和隐式积分法。
显式数值积分法(Explicit Numerical Integration)强调模拟的真实感,系统时间步长较小,每步的求解量较小,但迭代次数较多。
隐式数值积分法(Implicit Numerical Integration)可以使用较大的时间步长,减少迭代次数,但适用的范围有限。
(1)显式欧拉方法
显式欧拉算法是显式数值解法中最基本、最简单的算法,但是它的求解精度比较低。它是用向前差商来近似代替导数,所以也称为向前欧拉算法。
对于常微分方程:
y′(t)=f(x,y(t)),t∈[a,b]
y(a)=y0
可将区间[a,b]分成n段,每段的时间片分为h=(b-a)/n,方程在第t点有:y′(t)=f(t,y(t)),向前差商近似代替导数:![]() ,y(t)),则y(t)的近似值Y(t)为:
,y(t)),则y(t)的近似值Y(t)为:
Y(t)≈y(tn)=y(t0+nh)
将上式用泰勒级数展开:
![]()
在质点—弹簧模型中,应用显式欧拉法有以下公式:

其中:a是质点加速度,μ是质点质量,F是质点所受合力;(https://www.xing528.com)
v是质点速度,p是质点位置。
欧拉积分实际上是取自泰勒级数的前两项,因此,除非从二阶导数开始以后各项均为0,否则欧拉积分方法总会带来舍入误差,我们可以将误差记为o(h3),只要h取得适当小,就能将误差控制在所期望的范围内。
(2)龙格—库塔法
龙格—库塔(Runge-Kutta)法是一种在工程中应用广泛的高精度显式单步算法。此算法精度高,误差小,但是理论原理也较复杂。4阶Runge-Kutta计算公式如下:
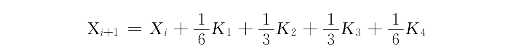

其中
![]()
龙格—库塔法是一个精确度和计算量妥协后的最佳选择,4阶Runge-Kutta需要经过4次函数计算,但可以得到O(h3)的精确度。
(3)Verlet积分法
法国物理学家Loup Verlet在1967年提出Verlet积分方法,该方法广泛应用于分子动力学仿真领域,它比欧拉积分法具有更好的稳定性而且更简单。
Verlet积分算法通过质点当前位置和上一时刻位置来计算下一时刻的质点位置,而不用速度,减少了错误,速度项是隐式地给出,因此该方法相对比较稳定。其计算公式如下:
x(t0+Δt)=2x(t0)-x(t0-Δt)+aΔt2
速度由下式隐式得到:
![]()
表4-2 几种数值积分方法比较

在织物虚拟模拟中,一般都选择显式积分的方法,因为显式的方法是一个标准的、精确的积分方法。显式方法的每一步都要比隐式方法快,并且显式方法易于和空间限制相结合,这些空间限制是指在织物造型系统中那些穿透的质点和被拉长的边。
本文也采用显示欧拉积分法对2-D裁片质点—弹簧系统进行数值求解。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




