理论与算法：基于[18，19]的探讨

小波分析是继傅里叶分析之后的一种新型信号分析方法，与傅里叶变换相比，它具有良好的时频局部分析特性和多尺度分析特性，被看成是数学领域半个世纪以来的工作结晶，因为具有多分辨率的特征，而且在时域和频域都具有表征信号局部特征的能力，被誉为数学显微镜或信号分析的显微镜。小波分析技术凭借多尺度分析和时频联合分析的优势，已在焊接领域中得到了应用。

设给定基本函数为ψ（t），令

式（4-9）中的a，b均为常数，且a＞0。ψ_a，b（t）函数是基本函数ψ（t）先作平移再作伸缩以后得到的，若a，b不断地变化，可得到一组基函数ψ_a，b（t）。对于能量有限信号x（t），即x（t）∈L²（R），则x（t）的小波变换（Wavelet Transform，WT）定义为

由于式（4-10）中的变量a、b、t均为连续变量。因此，式（4-10）又称为连续小波变换。式中的积分范围均为-∞到+∞。信号x（t）的小波变换WT_x（a，b）是a和b的函数，其中a为尺度因子，又称伸缩因子或压扩因子，b为平移因子或时移因子。ψ（t）称为基本小波，或称母小波。ψ_a，b（t）是母小波经位移和压扩所产生的一组函数，称之为小波基函数，或简称小波基。式（4-10）表达的小波变换WT_x（a，b）可以解释为信号x（t）和一组小波基函数的内积。基本小波ψ（t）可以是实函数，也可是复函数。而小波变换幅的平方则是一种能量分布，即

其中C_ψ为

式（4-11）为信号的尺度图，它是随着平移因子b和尺度因子a而变化的能量分布，而不是随t和ω变化的能量分布。

设信号x₁（t），x₂（t），函数ψ（t）∈L²（R），则小波变换的内积定理可以表示为

其中C_ψ为

Ψ（ω）为ψ（t）的傅里叶变换。式（4-13）称为容许条件或相容性条件，式（4-13）又称为小波变换中的Parseval定理。将式（4-12）改写为更简单的形式：

Ψ（ω）为ψ（t）的傅里叶变换。式（4-13）称为容许条件或相容性条件，式（4-13）又称为小波变换中的Parseval定理。将式（4-12）改写为更简单的形式：

设x₁（t）=x₂（t）=x（t），得

设x₁（t）=x₂（t）=x（t），得

式（4-15）表明，小波变换的幅平方在尺度—位移平面上的加权积分等于信号在时域的总能量，因此，小波变换的幅平方可以看作是信号能量时频分布的一种表达形式。

式（4-15）表明，小波变换的幅平方在尺度—位移平面上的加权积分等于信号在时域的总能量，因此，小波变换的幅平方可以看作是信号能量时频分布的一种表达形式。

定理：设x（t），ψ（t）∈L²（R），Ψ（ω）为ψ（t）的傅里叶变换，若容许条件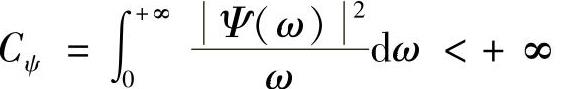成立，则x（t）可由其小波变换来恢复

定理：设x（t），ψ（t）∈L²（R），Ψ（ω）为ψ（t）的傅里叶变换，若容许条件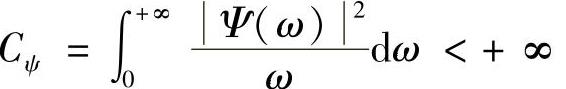成立，则x（t）可由其小波变换来恢复

式（4-16）就是小波变换后重建信号的理论基础，由于计算机只能处理离散信号，相应的小波变换应离散化。通常对a的离散化是采用幂级数的方法来逐级改变的，故令a=（a₀）j，a₀＞0，b=kb₀（a₀）j，j∈Z，通常设a₀＞1，所以对应的离散小波基函数为(www.xing528.com)

式（4-16）就是小波变换后重建信号的理论基础，由于计算机只能处理离散信号，相应的小波变换应离散化。通常对a的离散化是采用幂级数的方法来逐级改变的，故令a=（a₀）j，a₀＞0，b=kb₀（a₀）j，j∈Z，通常设a₀＞1，所以对应的离散小波基函数为

离散化小波变换的系数可表示为

离散化小波变换的系数可表示为

信号的重构公式为

其中，C是一个与信号无关的常数，式（4-17）、式（4-18）和式（4-19）就组成了离散化的小波变换和小波逆变换的公式，也是计算机进行离散化处理的理论基础。

如何选择常数a₀和b₀才能保证信号重构的精度呢？显然，常数a₀和b₀越小，对应的网格越密，信号重构的精度越高，反之，则信号的重构精度就越低。小波离散化的本质实际上是在尺度因子a和平移因子b组成的平面上进行的离散化。为了使小波变换具有可变化的时间和频率分辨率、适应信号的非平稳性，需要改变尺度因子a和平移因子b的大小，使小波变换具有变焦距的功能。实际上是采用动态的采样网格，最常用的就是二进制的动态采样网格。设a₀=2和b₀=1，则网格对应的尺度为2^j，平移为2^jk，于是小波基函数变为

ψ_j，k（t）=2^-j/2ψ（2^-jt-k），j，k∈Z （4-20）

式（4-20）称二进小波，设ψ_j，k（t）∈L²（R），ψ_j，k（t）的傅里叶变换为Ψ（ω），存在常数A，B，且0＜A＜B＜+∞使得稳定条件成立，即

其中，C是一个与信号无关的常数，式（4-17）、式（4-18）和式（4-19）就组成了离散化的小波变换和小波逆变换的公式，也是计算机进行离散化处理的理论基础。

如何选择常数a₀和b₀才能保证信号重构的精度呢？显然，常数a₀和b₀越小，对应的网格越密，信号重构的精度越高，反之，则信号的重构精度就越低。小波离散化的本质实际上是在尺度因子a和平移因子b组成的平面上进行的离散化。为了使小波变换具有可变化的时间和频率分辨率、适应信号的非平稳性，需要改变尺度因子a和平移因子b的大小，使小波变换具有变焦距的功能。实际上是采用动态的采样网格，最常用的就是二进制的动态采样网格。设a₀=2和b₀=1，则网格对应的尺度为2^j，平移为2^jk，于是小波基函数变为

ψ_j，k（t）=2^-j/2ψ（2^-jt-k），j，k∈Z （4-20）

式（4-20）称二进小波，设ψ_j，k（t）∈L²（R），ψ_j，k（t）的傅里叶变换为Ψ（ω），存在常数A，B，且0＜A＜B＜+∞使得稳定条件成立，即

二进小波变换可表示为

二进小波变换可表示为

信号的重构表达式为

信号的重构表达式为