轨道有限长度与压缩理论探讨

第三章介绍了如何通过时滞神经网络系统解轨道有限性并利用Cauchy收敛准则同时证明平衡点的存在性与全局稳定性.更一般地，考虑如下自治时滞常微分系统：

其中x∈ℝn，f：ℝn×ℝn→ℝn连续可微函数.令y=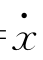，可得

若能通过（9.2）证明y（t）∈L1[0，+∞），则可以得到（9.1）的全局稳定性.进一步，如果｜y（t）｜=O（exp（-αt））（α＞0），那么可推出系统（9.1）的指数全局稳定性.

更进一步，考虑时滞时变（非自治）常微分系统

其初始条件为x（θ）=φ（θ），θ∈[-τ，0]，其中τ=maxj=1，…，mτj.考虑另一个解z（t），对应初始条件ψ（θ）.定义ρ（θ，λ）=λφ（θ）+（1-λ）ψ（θ），λ∈[0，1].设w（t，λ）是系统（9.3）在初始条件ρ（θ，λ）的解，v（t，λ）=∂w/∂λ，则(www.xing528.com)

如果当t→∞，v（t）关于0≤λ≤1一致收敛到零，则由

可得limt→∞‖x（t）-y（t）‖=0.这就证明了时滞时变系统的轨道稳定性.当v（t，λ）=O（exp（-αt））（α＞0不依赖λ），那么轨道是指数稳定的.

此方法可视为对有限轨道长度方法的推广，也可视为压缩原理（[1]～[3]）在时滞系统的推广.可以看出，在第四章和第六章关于周期和概周期解稳定性的分析方法本质上就是证明系统（9.4）的全局稳定性.