附录B：证明引理2-3

引理2-3　任意给定两个满秩矩阵A∈N×M和B∈N×K。根据文献[94]，矩阵对（AH，BH）的GSVD分解返回酉矩阵Ψ1∈M×M和Ψ2∈K×K，非负对角矩阵D1∈M×K和D2∈K×K，以及矩阵X∈N×K，rank{X}＝k。那么，

（1）Av＝Bw≠0成立当且仅当

其中，Γ（A）表示矩阵A的零空间的基向量；ys表示具有合适长度的任意非0向量；y1和y2表示具有合适长度的任意向量。

（2）满足Av＝Bw≠0线性无关的v的个数为s＋dim{null（A）}。(www.xing528.com)

证明：①根据GSVD分解可知，AΨ12Λ1－1＝BΨ22Λ2－1＝X2成立。因此，对于式（B-1）及式（B-2）给出的v和w来说，Av＝Bw成立。

接下来，我们应用反证法，证明仅当v∈span（Φ1）时，Av＝Bw成立，其中，Φ1≜[Ψ12Λ1－1　Γ（A）]。首先，假设存在这样的非零矢量，且满足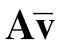＝Bw。那么，可以判断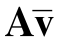∉span（AΦ1）；否则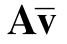，＝AΦ1x，这表明，v－Φ1x＝Γ（A）y1，因此span（Φ1），这与假设相互矛盾。另一方面，由于＝Bw，∈span（X2）成立。联立由GSVD分解可知，span（x2）＝span（AΦ1），因此∈span（AΦ1）。这与∉span（AΦ1）相互矛盾。综上所述，仅当v∈span（Φ1）时，Av＝Bw成立。关于w的论证，有类似情况。

②根据GSVD分解可知，AΨ11＝0，因此span（Ψ11）⊂span（Γ（A））成立。此外，根据矩阵理论可知，rank{Ψ11}＝M－r－s＝M－min{M，N}＝（M－N）＋，这表明，span（Ψ11）中线性无关的矢量数与span（Γ（A））中的相同。因此，span（Ψ12∩span（Γ（A））＝0。又，由于Ψ1是一个酉矩阵，span（Ψ12）∩span（Ψ11）＝0成立。因此，span（Ψ12）∩span（Γ（A））＝0。联立式（B-1）可知，满足Av＝Bw＝0线性无关的v的个数为s＋dim{null（A）}。