运用函数与方程思想解数列问题的优化方法

数列是定义在正整数集或其有限子集上的特殊函数，当然离不开对其函数性质如单调性、最大最小项、周期性的研究，数列的通项公式和前n项和公式是关于n的函数，也可以将其转化为方程或方程组，等差、等比数列中的“知三求二”计算问题也常用解方程(组)的方法求解，运用函数与方程思想解数列问题的题型主要表现在研究数列的最值问题、范围问题以及数列不等式的证明.

例1　在等差数列{an}中，已知S100=10，S10=100，求S110.

解题策略　一个数学问题可以从不同的视角进行分析，本题可以套用公式，列方程，用方程组的“通性通法”求解；可以由公差不为0的等差数列前n项和这个公式，结合二次函数的性质求解；可以创造一个“和数列”，即对等差数列{an}每10项分成一组，每组的和作为一项构造新数列：S10，S20-S10，S30-S20，…，S100-S90仍然是一个等差数列，以此求解；可以根据等差数列的性质，即m，n，p，q∈N*，且m+n=p+q，则am+an=ap+aq进行整体代换求解；还可以构造这一关于n的一次函数，利用点共线求解.基础题型，解法多样，函数与方程的思想这一主线贯穿其中，可拓展“多元解题策略”的视野，供读者赏析.

解法一　设数列{an}的公差为d，则

　解得

解法二　设Sn=an2+bn(a≠0)，则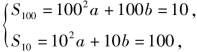解得

从而

解法三　将数列依照原有的顺序每10项分为一组，每组的和作为一项构造新数列：S10，S20-S10，S30-S20，…，S100-S90，则这个数列是一个首项为S10，第10项为S100-S90的等差数列，设新数列的公差为d′，则该数列的前10项和等于S100.

解得d′=-22.

该数列前11项和

解法四　

又由

解法五　形式上是关于n的“一次函数”.

∴点共线.

则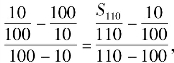解得S110=-110.

例2　已知数列{an}满足且

(1)求证：

(2)设数列的前n项和为Sn，求证：

解题策略　本题将数列递推公式与不等式、函数及其最值等知识相结合.集中考查归纳猜想、构造转化、分类讨论等数学思想方法的运用，技巧性较强，要求考生具备较强的思维能力和运算变形能力，如将递推公式转化为在利用反比例函数时先求函数定义域将Sn转化为含有an+1的表达式，再结合已知条件求出an+1的取值范围都体现了转化与函数思想的运用.

证明　(1)由题意得即

由an=(1-an-1)an-1得an=(1-an-1)(1-an-2)…(1-a1)a1>0.

由得即

(2)由题意得

故

由得

又由(1)知

即

以上各式相加得

即

即

例3　已知数列{an}的各项均为正数，其前n项和为Sn，且对任意n∈N*，有

(1)求数列{an}的通项公式；

(2)设bn=2n(n∈N*)，对每个正整数k，在bk与bk+1之间插入ak个1，得到一个新的数列{cn}，记数列{cn}的前m项和为Tm，求使得Tm=2cm+1成立的所有正整数m的值.

解题策略　第(1)问，由an=Sn-Sn-1，把条件代入得an与an-1的关系，从而求得{an}的通项公式；第(2)问是探究性问题，可采用二项展开式及不等式放缩的技巧进行探究，以寻找正整数m的值是否存在.(www.xing528.com)

解：(1)当n=1时，由及a1为正数，得a1=2；

当n≥2时，由

得(an+an-1)(an-an-1-2)=0，　∵an+an-1>0，　∴an-an-1=2.

故{an}是首项和公差均为2的等差数列.

∴an=2+(n-1)·2=2n(n∈N*).

(2)当m=1时，T1=c1=b1=2，2c2=2×1=2，满足要求.

当m≥2时，若cm+1=1，则Tm≥T2=3>2cm+1，不满足要求；

若cm+1≠1，则cm+1必为数列{bn}中的某一项，不妨设cm+1=2k+1(k∈N*).

于是Tm=(b1+b2+…+bk)+(a1+a2+…+ak)

=(2+22+…+2k)+(2+4+…+2k)=2k+1+k2+k-2.

由Tm=2cm+1，得2k+1+k2+k-2=2×2k+1即2k+1=k2+k-2(k∈N*).　①

显然，k=1不满足①，则当k≥2时，有

∴方程①无正整数解.

综上所述，满足条件的正整数m只有一个，即m=1.

例4　已知函数的最大值不大于又当时，

(1)求a的值；

(2)设证明

解题策略　将函数嵌入数列综合题中，突显数列综合应用的多元切入点，是高考命题的热点，本例以函数性质的研究为背景与数列知识融为一体，又汇集了不等式的证明，数学归纳法，在整个解题过程中函数的思想方法始终贯穿其中，是一道精彩纷呈的好题.

解：(1)由于的最大值不大于即a2≤1.　①

又当时，　即解得a≥1.　②

由①和②得a=1.

(2)证法一　❶当n=1时，不等式成立；

故n=2时不等式也成立.

❷假设当n=k(k≥2)时，不等式成立，

的对称轴为知f(x)在上为增函数，

∴由得

即当n=k+1时，不等式也成立.

根据 ❶和 ❷可知，对任何n∈N*，不等式成立.

证法二　❶当n=1时，不等式成立；

❷假设当n=k(k≥1)时不等式成立，即

则当n=k+1时，

于是因此当n=k+1时，不等式也成立.

根据 ❶和 ❷可知，对任何n∈N*，不等式成立.