【摘要】:练习图31-1中所示为一个承受均匀面积载荷的三明治板。变量是蒙皮的厚度以及上下板间的距离h。由方程式可有:2t优化·ρH=h优化·ρK 其中,情形b:支承结构的抗弯刚度给定要求的刚度为由此可以直接得出变量:将该变量代入重量方程,则可得出自重为现在来确定另外一个变量。重量最小化要求为即因此,最小重量可计算为从以上计算可以看出,当刚度给定时,只有形芯的重量增加一倍,才能达到重量最小化。
练习图31-1中所示为一个承受均匀面积载荷的三明治板。这里考虑对其自重加以优化。变量是蒙皮的厚度以及上下板间的距离h。
现在,根据所要求的承载能力和刚度分别来进行优化。
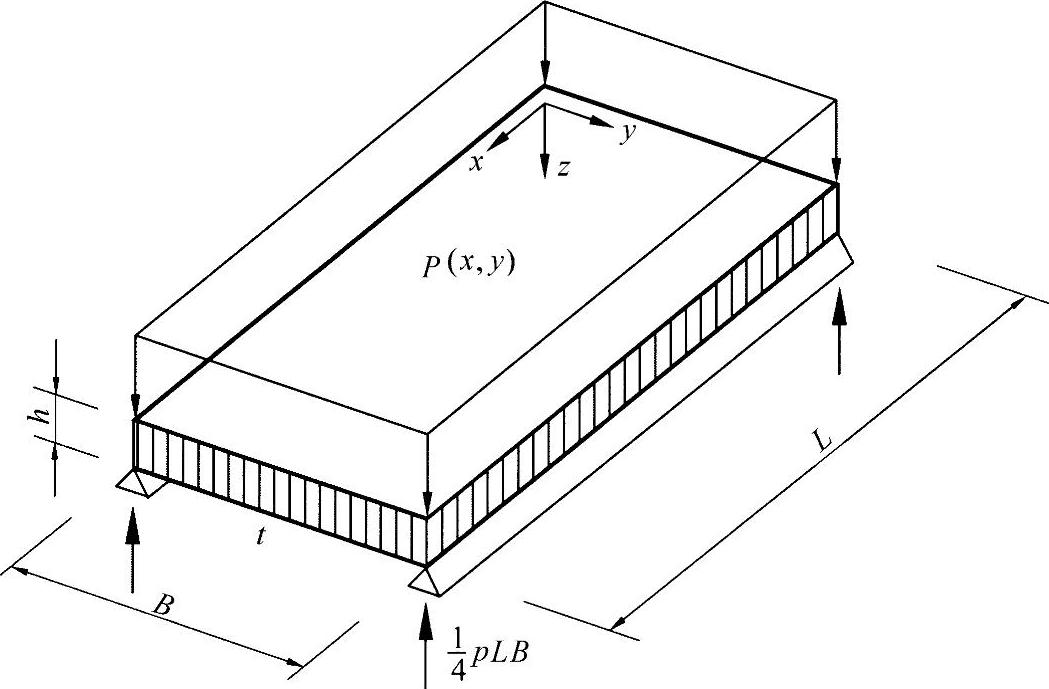
练习图31-1
三明治板材的重力为
G=g·B·L(2t·ρH+h·ρK) (1)
情形a:桁梁承载能力给定
在蒙皮中的应力要求为

对于重量优化的几何尺寸,其前提条件为,在蒙皮中产生的弯曲应力正好为允许值:

平板的面积惯性矩为
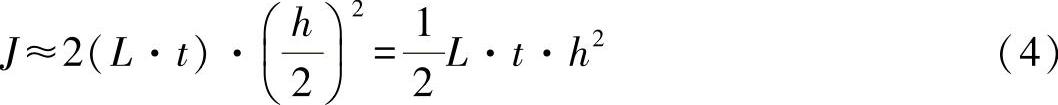
在平板中心产生的弯曲力矩的最大值为
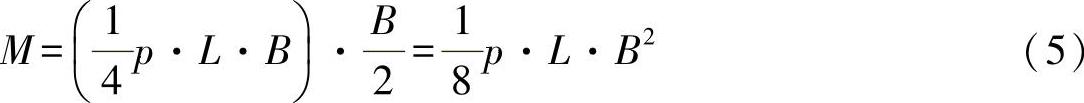
可得出应力:
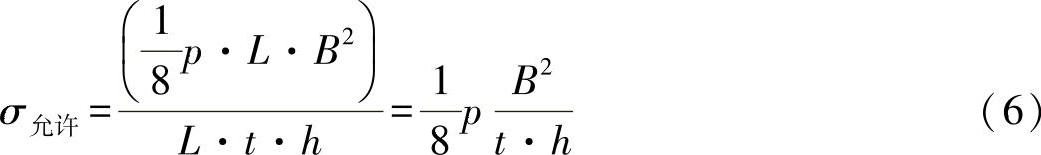
也可确定一个变量:

代入方程式(1),可得出重量为
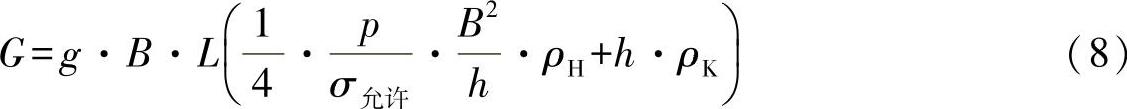
由下述要求:
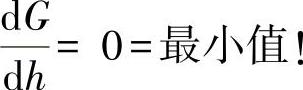
或者
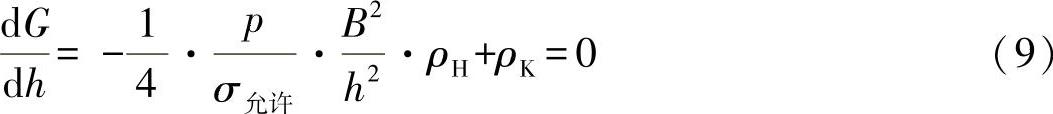
可得出第二个变量:(https://www.xing528.com)
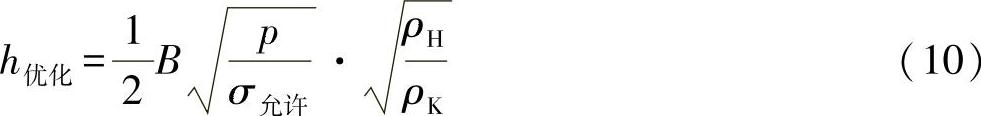
现在代入这些参数,则可以得出最小重量为
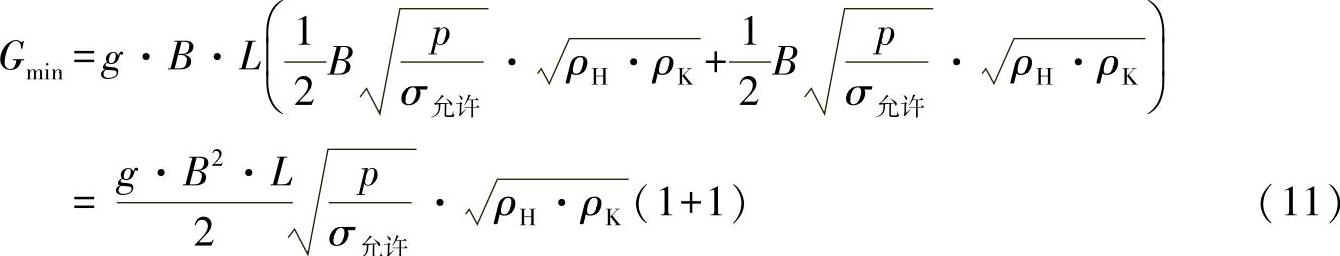
从中可以推导出,对于给出的承载能力要求,在蒙皮与形芯重量相同的情形下,可以实现重量最小化。由方程式(1)可有:
2t优化·ρH=h优化·ρK (12)
其中,

情形b:支承结构的抗弯刚度给定
要求的刚度为
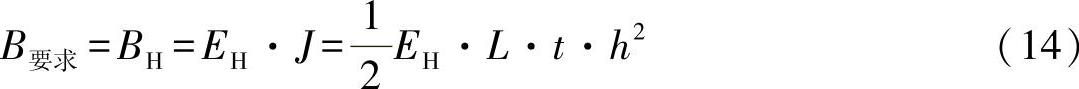
由此可以直接得出变量:

将该变量代入重量方程,则可得出自重为
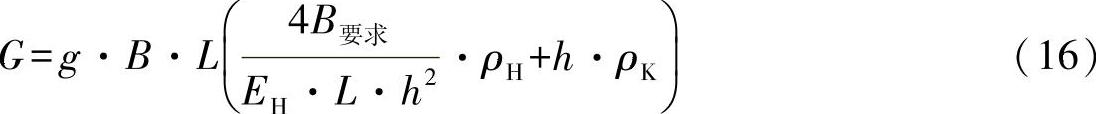
现在来确定另外一个变量。重量最小化要求为
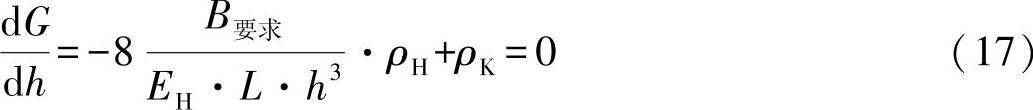
即

因此,最小重量可计算为
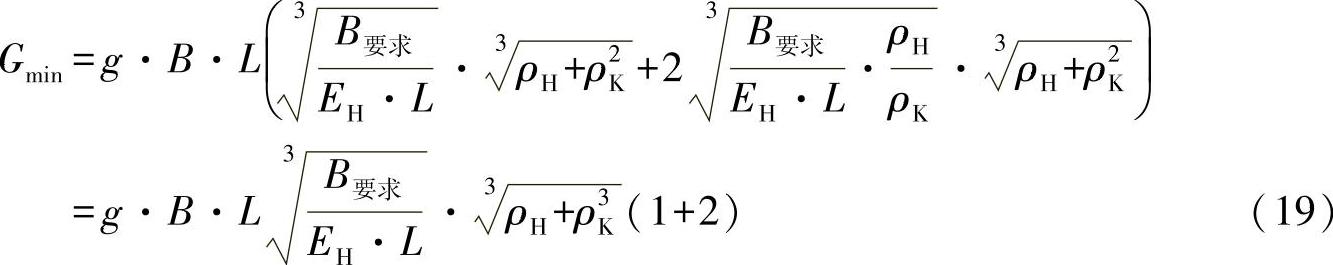
从以上计算可以看出,当刚度给定时,只有形芯的重量增加一倍,才能达到重量最小化。因此,有如下关系:

从中可以推导出,必有:
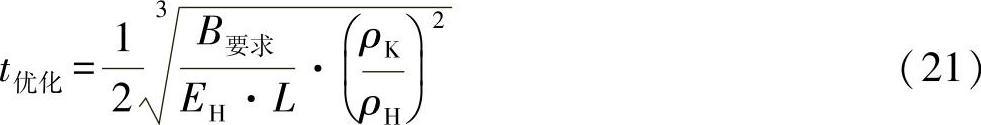
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




