利用凸函数性质证明不等式

凸（凹）函数常见的定义是如下的定义1和定义2，可以证明两者是等价的.

定义1 设f（x）在区间I上连续，若对I上任意两点x₁，x₂，总成立

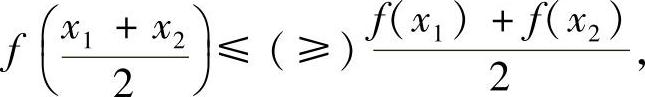
则称f（x）是I上的凸（凹）函数.

定义2 设f（x）是定义在区间I上的函数，若对I上任意两点x₁，x₂和实数λ∈（0，1），总成立

f（λx₁+（1-λ）x₂）≤（≥）λf（x₁）+（1-λ）f（x₂），

则称f（x）是I上的凸（凹）函数.

凸函数的基本性质

1.f为区间I上凸函数的充要条件是：对I上任意三点x₁<x₂<x₃，总有

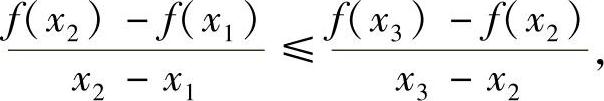
或

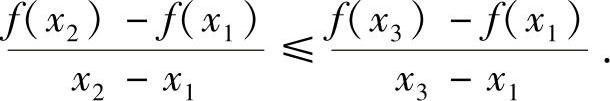
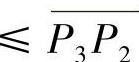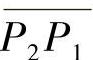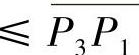如图8-2所示，这个性质的几何意义是明显的，即f为I上的凸函数⇔P₂P₁的斜率的斜率或的斜率的斜率.

2.若f（x）在区间I上二阶可导，则下面关于凸函数的四个命题等价：

（1）f是I上的凸函数；

（2）f′在I上单调递增；

（3）f（x）≥f（x₀）+f′（x₀）（x-x₀），∀x₀∈I，其几何意义是：切线在曲线下方；

（4）f″≥0.

值得大家注意的是，凸函数的定义2是借助于几何直观来定义，即“弦在曲线的上方”.我们利用凸函数的性质证明不等式，主要是用曲线在切线或弦的一侧这一几何特性来实现的！因此，在做题时，大家要尽量借助几何直观来思考！

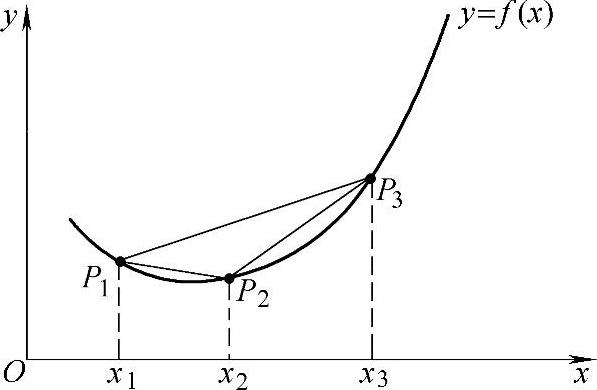
图 8-2

例8.10 詹森（Jensen）不等式 设f是区间I上的凸函数，则∀x₁，x₂，…，x_n∈I和λ₁，λ₂，…，λ_n>0，且λ₁+λ₂+…+λ_n=1，都有

证明 用数学归纳法.当n=2时，这正是凸函数的定义2.设n=k≥2时命题成立，将证n=k+1时，命题也成立.

设x₁，x₂，…，x_k+1∈I及λ₁，λ2，…，λ_k+1>0，且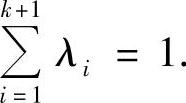令

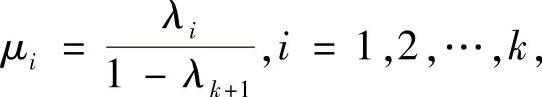
易见μ_i>0且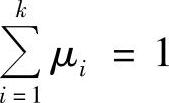，此时还有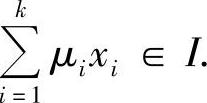利用n=2及n=k≥2的结论可得

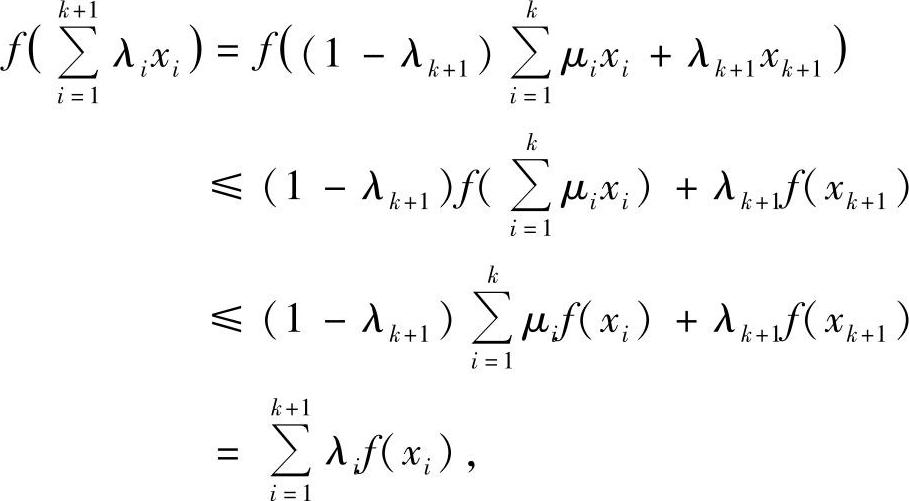
综上知，结论成立.

注8.3 1.詹森不等式有下面更为一般的形式：设f在区间I上是凸函数，则∀x₁，x₂，…，x_n∈I及β₁，β₂，…，β_n>0，都有

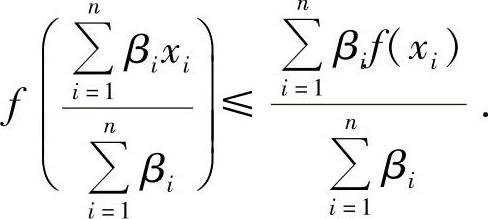
提示 在例8.10中，令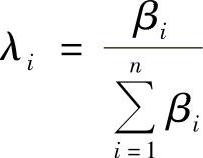，i=1，2，…，n，立即可得结论.

2.在例8.10中若取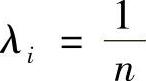，则结论变为

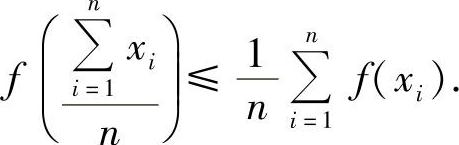
这个不等式会经常用到，在f′（x）存在的情况下，对它我们也可用如下方法证明.

令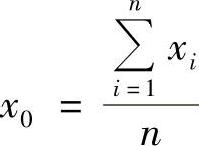，由凸函数f的性质，有

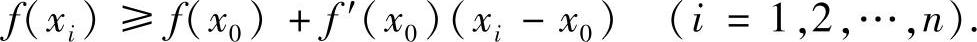
对上面n个不等式作和，可得

此即为欲证的不等式.

例8.11 设Φ（x）是[m，M]上的有界凸函数，f（x），p（x）在[a，b]上可积，且m≤f（x）≤M，p（x）≥0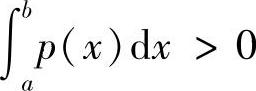，，证明不等式

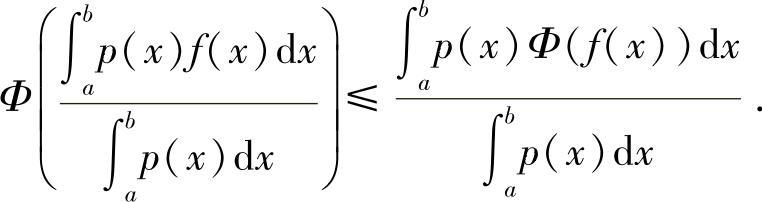
证明 将区间[a，b]n等分，记分点为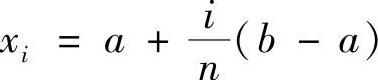，i=0，1，…，n.∀ξ_i∈[x_i-1，x_i]，记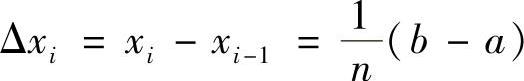，将积分写成积分和得

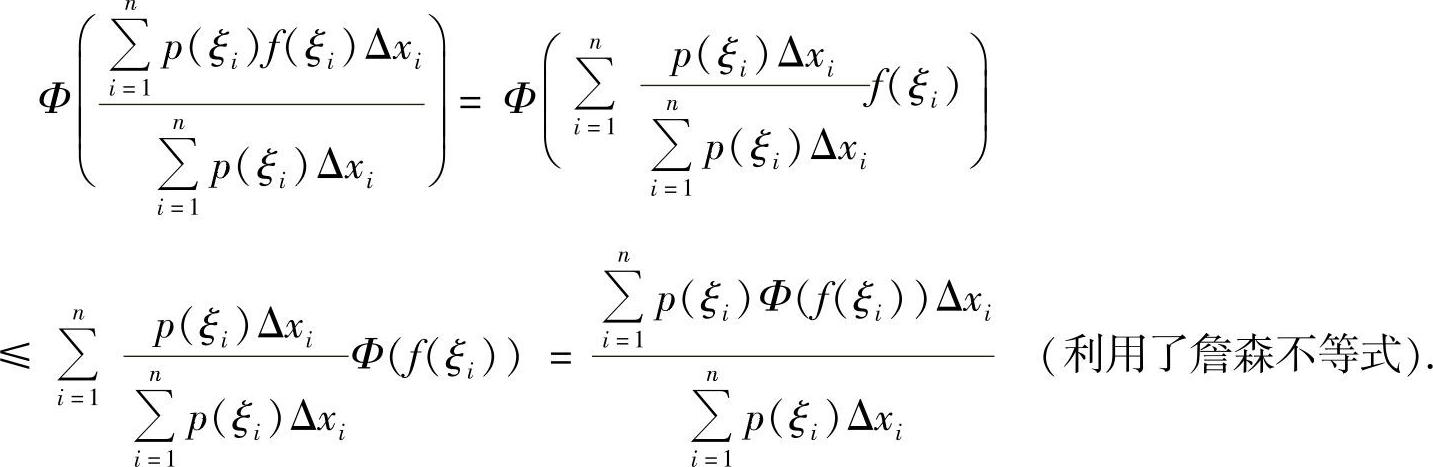
因为Φ（x）是[m，M]上的凸函数，所以Φ（x）在[m，M]上连续.注意到f，p的可积性，在上式中令n→∞可得结论.

类题1 若f（x）在[a，b]上连续，且f（x）>0，证明：

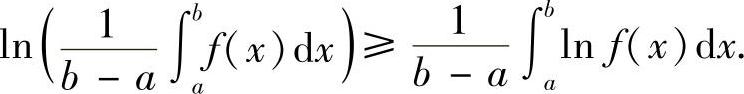
提示 利用lnx在（0，+∞）上是凹函数，仿例8.11可证之.

类题2 设函数f（x）在R上处处二阶可微，且f″（x）≥0，u=u（t）为任一连续函数.证明

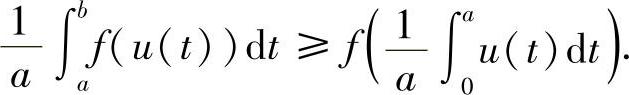
提示　此题是例8.11的特例.将例8.11中的Φ换成f，f换成u，取p（x）=1即可.

类题3　设F（x）在（-∞，+∞）上有定义，F″（x）>0，f（x）为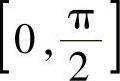上的连续函数，证明：

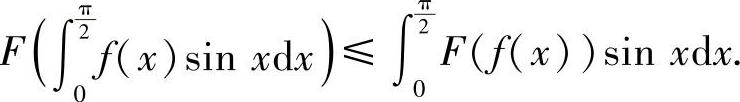
提示　此题也是例8.11的特例.取p（x）=sinx，并注意到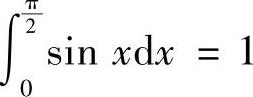即可.

例8.12　阿达玛（Hadamard）不等式　设f（x）是[a，b]上的凸函数，证明：

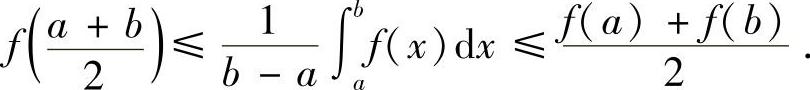
证明　先证左边的不等式.由第四讲中定积分的计算技巧知，

此即为

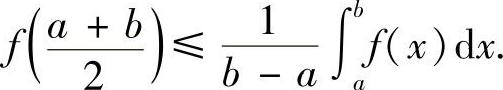
再证右边的不等式.作变量替换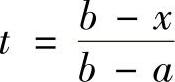，则

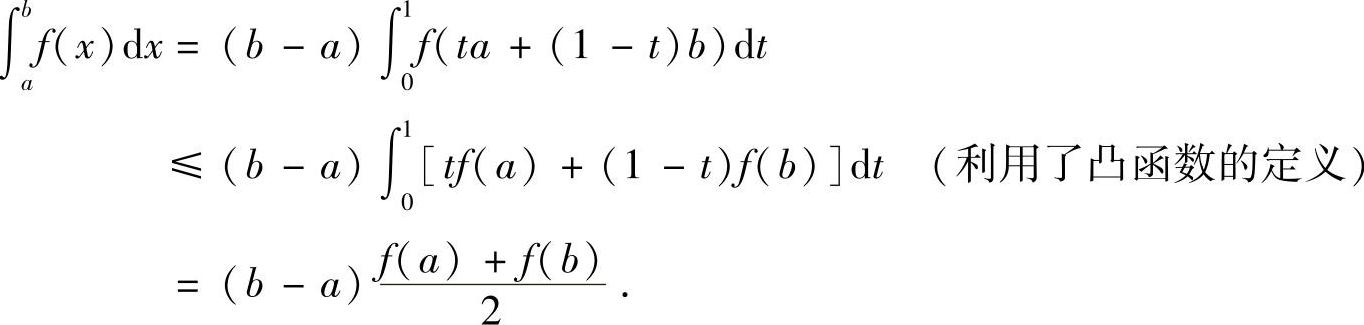
类题　证明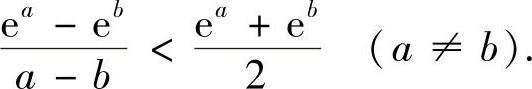：(https://www.xing528.com)

例8.13　设f（x）在[a，b]上二阶可导，且f（x）≥0，f″（x）<0.证明：

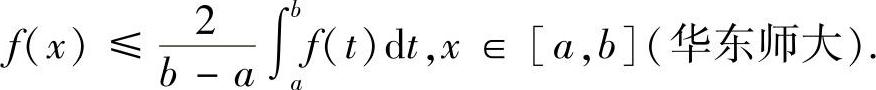
证明　由已知条件可知，f（x）是[a，b]上的严格凹函数.设x₀∈[a，b]是f（x）的最大值点，则必有f（x₀）>0.由凹函数的性质，对任意的x∈[a，b]，有

f（x₀）≤f（x）+f′（x）（x₀-x）.

对上式两边在[a，b]上积分，可得：

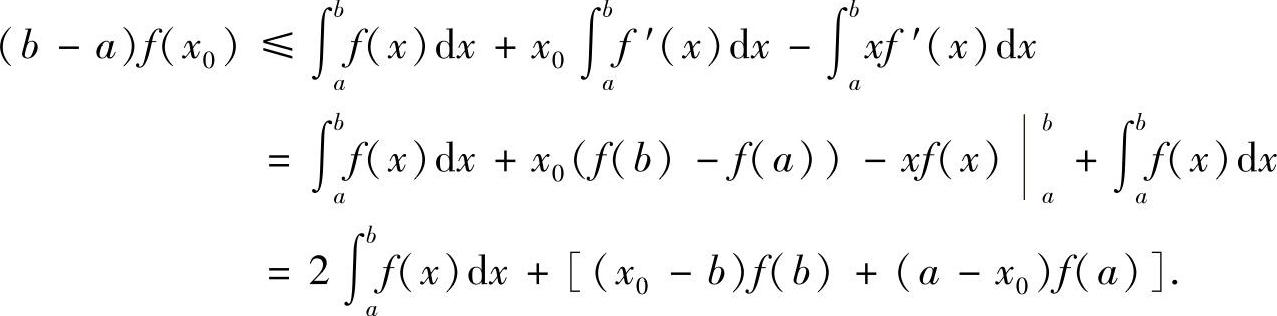
注意到（x₀-b）f（b）+（a-x₀）f（a）≤0，有

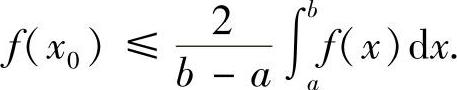
从而，对任意的x∈[a，b]，有

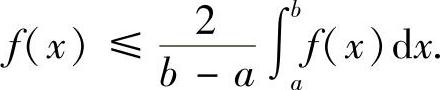
例8.14 设f（x）在[0，1]上是凸函数，f（0）>f（1），证明：

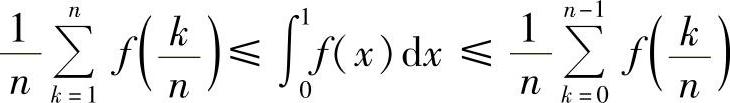
对充分大的n成立.

证明 由例8.12的右边不等式知，

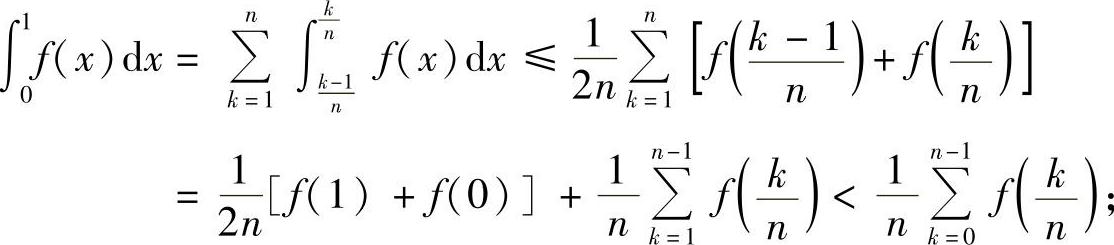
另一方面，由例8.12的左边不等式有，

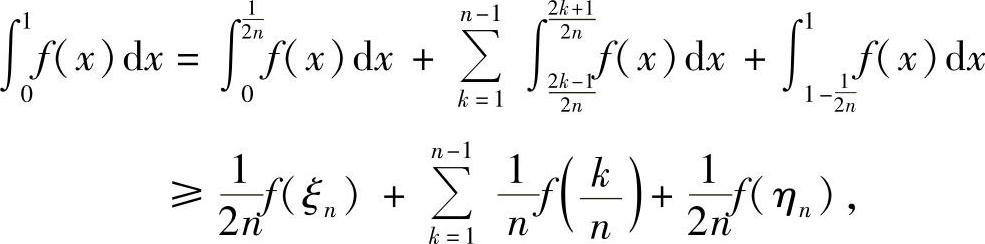
这里对上式右边的第一、第三项应用了积分中值定理，其中，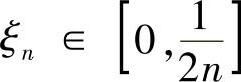

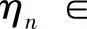
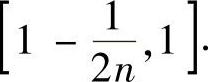
下面只需证明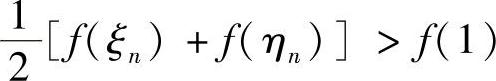即可.由f的连续性及ξ_n→0，η_n→1（n→∞），并注意到

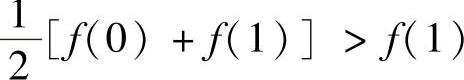
可知，∃N>n，当n>N时，有

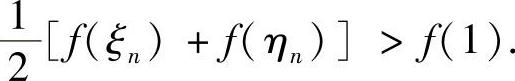
例8.15 设a>0，b>0，证明：

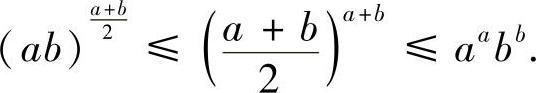
证明 左边的不等式显然成立，下面证明右边的不等式.

取f（x）=xlnx，则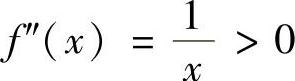，x∈（0，+∞），即f（x）是（0，+∞）上的凸函数，故由

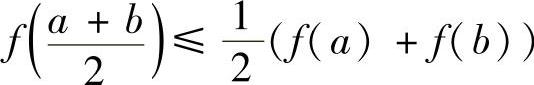
可得

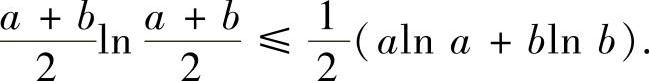
由此可得右边的不等式.

例8.16 设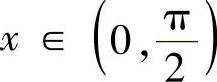，证明：

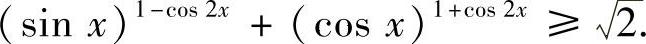
证明 原不等式等价于

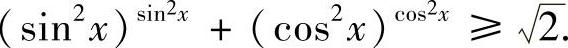
取f（x）=x^x，x∈（0，+∞），则由f″（x）=x^x-1[x（lnx+1）2+1]>0可知，f（x）是（0，+∞）上的凸函数.若记a=sin²x，b=cos²x，由凸函数的性质

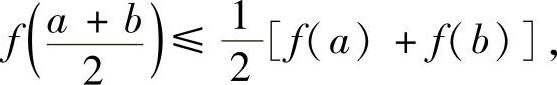
即

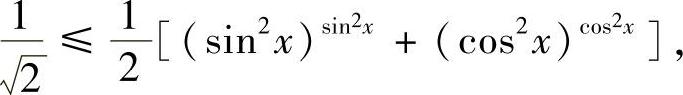
亦即

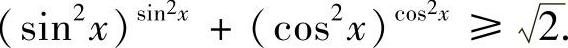
类题1 证明不等式

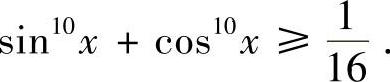
提示 取f（x）=x⁵，易见f（x）是凸函数，利用凸函数的性质可得结论.

类题2 设a，b，c>0，证明不等式：

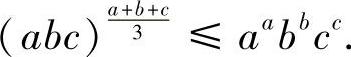
提示 取f（x）=xlnx，则f（x）是凸函数.于是，有

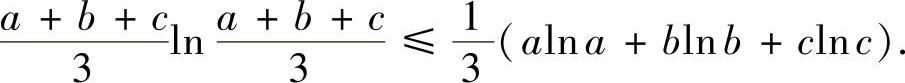
利用平均值不等式，有

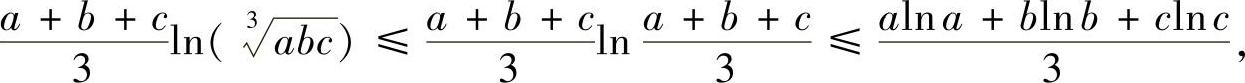
此即为结论.

例8.17 设a，b>0，a≠b，证明不等式

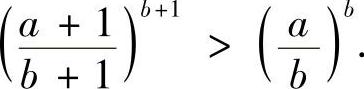
证明 不妨设a>b>0，用两种方法来证.

证法1 用凸函数的性质来证.原不等式等价于

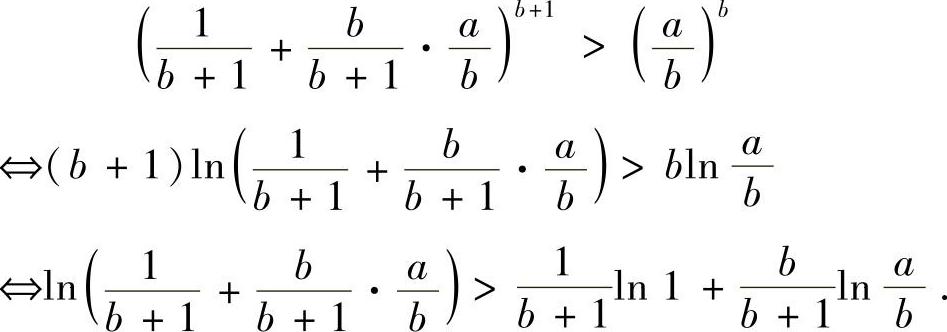
注意到-lnx是凸函数，由凸函数的性质易知上式成立.

证法2 用函数的单调性来证.原不等式等价于

（b+1）[ln（a+1）-ln（b+1）]>b（lna-lnb）.

令

f（a）=（b+1）[ln（a+1）-ln（b+1）]-b（lna-lnb），a>b>0，由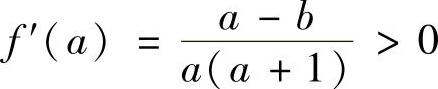知，f（a）在a>b上严格单增，故

f（a）>f（b）=0.

从而原不等式成立.