理解定积分：从无限细分到曲边梯形面积

定积分概念

【引例】连续曲线y=f（x）（x≥0）与x=a，x=b 及x轴围成的图形称作曲边梯形，如图1-3所示.

不难看出，曲边梯形的面积取决于区间[a，b]及定义在这个区间上的函数f（x）.由于f（x）在[a，b]上是连续函数，当x变化不大时，f（x）的变化也不大.因此，如果把区间[a，b]无限地细分，使每个小区间的长度无限趋于零，则小矩形的面积之和就是曲边梯形面积的近似值，如图1-4所示.

图1-3

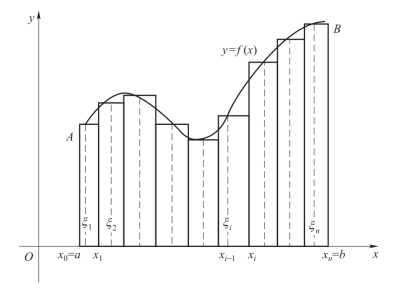
图1-4

具体的计算过程分为以下四步.

（1）分割：把[a，b]用分点a=x0＜x1＜x2＜…＜xn-1＜xn =b 分成n个小区间[x0，x1]，[x1，x2]，…，[xn-1，xn ]，每一个小区间的长度为Δxi=xi-xi-1（i=1，2，…，n），相应的曲边梯形被分割成n个小曲边梯形.

（2）近似代替：在每一个小区间[xi-1，xi ]（i=1，2，…，n）上任取一点ξi，以这些小区间的长为底、ξi处的值f（ξi）为高的小矩形代替相应的小曲边梯形，则各小曲边梯形面积的近似值为ΔSi ≈f（ξi）Δxi （i=1，2，…，n）.

（3）求和：把这n个小矩形面积相加，得到曲边梯形面积S的近似值为

（4）取极限：把区间[a，b]无限细分，使区间长度无限接近于0，这时小矩形面积之和的极限值就是曲边梯形的面积，即

式中，表示所有小区间长度Δxi的最大值，即，即表示每个小区间长度都无限接近于0.

1.定积分的定义

定义 1 设函数f（x）在区间[a，b]上有界，任取分点a=x0＜x1＜x2＜···＜xn-1＜xn =b，分[a，b]为n个小区间[xi-1，xi ]（i=1，2，…，n），记Δxi=xi-xi-1（i=1，2，3，…，n），，在每个小区间[xi-1，xi ]上任取一点ξi，作乘积f（ξi）Δxi 的和式.如果λ→0，上述和式的极限存在，则称此极限值为函数f（x）在区间[a，b]上的定积分，记作(www.xing528.com)

式中，x为积分变量；f（x）为被积函数；f（x）dx为被积表达式；[a，b]为积分区间，a为积分下限，b为积分上限；∫为积分号.

注意：（1）定积分表示一个数，它只取决于被积函数与积分区间，而与积分变量的记法无关，即

（2）如果a＞b，则.特别地，当a=b时，.

2.定积分的几何意义

当f（x）≥0时，定积分表示由曲线y=f（x），直线x=a，x=b及x轴所围成的曲边梯形的面积S，即

当f（x）≤0时，，如图1-5所示.

定积分的几何意义：由曲线y=f（x），直线x=a，x=b及x轴所围成图形的各部分面积的代数和，即在x轴上方的图形面积与在x轴下方的图形面积之差，如图1-6所示.

图1-5

图1-6

【例1】用定积分表示曲线（图1-7和图1-8）所围图形的面积.

图1-7

图1-8