最大流问题解决的Ford-Fulkerson方法

研究网络流量问题是实践中经常遇到的现实问题，例如交通网络中的车辆流、控制系统中的信息流、供水网络中的水流量、金融网络中的现金流等。

最大流问题是网络理论中的经典问题：在不违背容量限制的条件下，寻找一个流量方案，使得把物质从源点传输到汇点通过的网络流量最大。

下面首先介绍网络流的基本定义。

网络是一个加权的有向图D =〈V ,A, C〉，其中有向弧(i,j)的权Cij=C (i ,j)是一个非负数，称为(i,j)的容量，如果(i,j)∉E，可以规定Cij=0。假定在网络中有一点s处有物资需要运输到另一点t处，则称s为网络的源点，t为网络的汇点。

与网络相关的一个概念是流。网络上的流，是定义在弧集合A上的一个函数f：fij =f (i,j)，它满足以下性质：

（1）容量限制：∀i ,j ∈V,0＜fij＜Cij ；

设f为可行流，若fij =0，称(i,j)为f零弧；若fij=Cij ，称(i,j)为f饱和弧。而fij＞0的弧称为非零弧；fij＜Cij 的弧称为非饱和弧。

设P是一条以s为起点、t为终点的路，则路上的弧被分为两类，与路的方向一致的弧称为前向弧，与路的方向相反的弧称为后向弧。如果P的前向弧都是f非饱和弧，后向弧都是f非零弧，则称P为f增广路。

若P为f增广路，记P的前向弧集合为1A，后向弧集合为2A，令

由增广路的定义知，δ＞0。

定理1 （增广路定理）设f是网络的可行流，则f是最大流当且仅当不存在关于f的增广路。

定理2 （整数定理）若弧容量Cij都是正整数，则一定存在一个整数最大流。

本节主要介绍解决最大流问题的Ford-Fulkerson方法。

Ford-Fulkerson算法的基本思想：Ford-Fulkerson算法是一种迭代算法，首先对图中所有顶点对的流大小清零，此时的网络流大小也为0。在每次迭代中，通过寻找一条增广路径（Argument Path）来增加流的值。增广路径可以看作是源点s到汇点t的一条路径，并且沿着这条路径可以增加更多的流。迭代直至无法再找到增广路径位置，此时必然从源点到汇点的所有路径中都至少有一条边的满边（即边的流的大小等于边的容量大小）。

根据整数定理，当Cij都是正整数时，一定能在有限步内求出网络的最大流。算法的关键是求增广路径。

算法过程：

第一步：任意求出网络D的一个可行流f={fij}，通常取零流。(www.xing528.com)

初始化，源点s标号为(Δ,∞)，规定s为未检查顶点。每个顶点有2个标号，第一个标号表示前驱顶点，第二个标号为δ，表示在可能的增广路上可以调整的流量。

第二步：求f增广路。

（1）如果所有已标号顶点都已检查过，转到第四步；否则，任取一个已标号未检查的顶点vi，检查所有与vi关联的弧。

对有向弧(i,j)，如果vj未标号，且fij＜Cij ，给vj标号(vi,δ)，其中，δ=min{δ(i),Cij-fij }，表示弧(i,j)上可增加的流量；

对有向弧(j,i)，如果vj未标号，且fji ＞0，给vj标号(-vi,δ)，其中，δ=min{δ(i ),f ji},表示弧(i,j)上可减少的流量；

当所有与vi关联的弧都检查完毕，称vi已检查。

（2）如果已经得到标号，则一条增广路已经找到，转到第三步，否则返回第二步。第三步：调整过程。

（1）令vj=t。

（2）若vj标号为(vi,δ)，令fij=fij +δ(j )，vj=vi ；若vj标号为(-vi,δ)，fji=fji-δ(j )，vj=vi。

（3）若vj标号为(0,δ)，则vj=s，增广结束，把全部标号去掉，返回第二步，否则转到（2）。

第四步：重复以上过程，直到无法进行为止，算法结束，所得即为最大流。

例1（运输方案的设计） 图3.4.1中，s表示货源地，t表示目的地，弧表示交通线路，数字表示运输能力，现从s地发货运往t地，问如何设计运输方案，可达到最大流量？

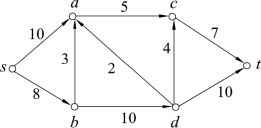
图3.4.1

解 应用Ford-Fulkerson算法编写MATLAB程序如下：