定义1.3.8 设(L,≤)是偏序集,如果对L中任意两个元a与b,inf {a,b}和sup {a,b}恒存在,则称(L,≤)为格(lattice).有时为了明确,格(L,≤)也常记为三元对的形式(L,∧,∨).
注1.3.2 在格(L,≤)中,inf {a,b}和sup {a,b}常分别记为a∧b和a∨b.
注1.3.3 一般地,在偏序集(P,≤)中,{x, y}⊆P的上(下)确界未必存在.于是当a∧b存在时,通常称(P,∧)为∧半格(∧-semi-lattice);当a∨b存在时,通常称(P,∨)为∨半格(∨-semi-lattice).从而,偏序集(P,≤)构成格当且仅当P既构成∧半格又构成∨半格.
定理1.3.3 设(L,≤)是格,则下列各结论成立:
(1)设X是L的非空有限子集,则inf X和sup X都存在;
(2)交换律(commutative laws)
![]()
(3)结合律(associative laws)
![]()
(4)幂等律(idempotent laws)
![]()
(5)吸收律(absorption laws)
![]()
(6)格序关联性质(lattice order relation property)
![]()
设(L,≤)是格,有时(L,∧,∨)可能仅有最大元max L,或仅有最小元min L,或兼而有之.从代数学观点看,格(L,∧,∨)可能有特殊的常值元.如果存在某个元1∈L使得对任意的a∈L都有a∧1=a,则称1是L的单位元,易证单位元存在时是唯一的.对偶地,如果存在某个元0∈L使得对任意的a∈L都有a∨0=a,则称0是L的零元,零元存在时也是唯一的.由定理1.3.3中(6)可知单位元即为最大元,零元即为最小元.既有最大元又有最小元的格(L,∧,∨)称为有界格,记为(L,∧,∨,0,1).一般地,有限格总是有界格.
定义1.3.9 设(L,≤)是偏序集,如果对L的任一子集X,inf X和sup X都存在,则称(L,≤)为完备格(complete lattice).
注1.3.4 完备格(L,≤)有最大元1,即1=sup L,也有最小元0,即0=sup∅.例1.3.8 格和完备格的若干实例.
(1)全序集一定是格.特别地,仅含两个元素0和1的全序集{0,1}是格.
![]()
(3)([0,1],≤)是完备格.
(4)(P(X),⊆)是完备格,通常称之为幂集格(power set lattice).
(5)设(L,≤)是格,且L含有有限多个元素,则(L,≤)是完备格.为此只需说明L的空子集∅有上确界和下确界.事实上,有限格有最大元1和最小元0,所以sup∅=0和inf∅=1都存在.
(6)图1.1中的(b)、(c)和(d)都是完备格.
定义1.3.10 设(L,≤)是格且∅≠M ⊆L.若M满足:
![]()
则称M是L的子格(sub-lattice).
利用子格的概念,可以通过已知格获得许多新的格.因此,通过求已知格的子格是获得新格的重要方法之一.如利用定理1.3.3中的幂等律可知,格的单元子集都是子格;格的子集是链时,其也是子格的例子.
定义1.3.11 设(L,≤)是格,如果对L中任意的元素a,b, c∈L,下列分配律之一成立:分配律(distributive laws)
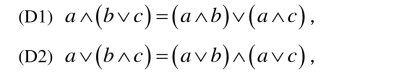
则称(L,≤)是分配格(distributive lattice).
注1.3.5 在定义1.3.11中,分配律(D1)和(D2)是相互等价的.事实上,设(D1)成立,则(D2)的正确性可如下验证:
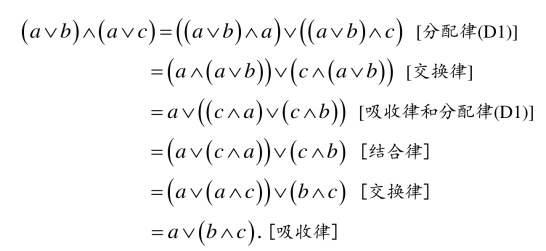
同样,设(D2)成立,则(D1)的正确性可如下验证:
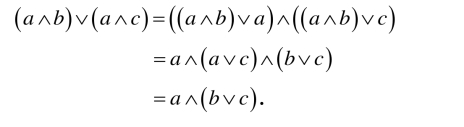
还需指出的是,在具体验证(D1)和(D2)时,应该注意到下列不等式总是成立的:

换言之,当验证了与(Ine1)和(Ine2)相反的两个不等式之一成立后,则(D1)或(D2)就已验证完成,进而(D1)和(D2)就同时成立了.注意到这一事实,可以大大节省证明过程的工作量.
定理1.3.4 全序集都是分配格.
在分配格中,下面的结论在验证某些特殊元的唯一性方面非常实用.
定理1.3.5 设(L,≤)是分配格,则下列推理成立:
![]()
证明 设a ∨b =c ∨b且a ∧b =c ∧b,则


然而
![]()
例1.3.10 设L={0,a, b, c,1},其上偏序关系≤按图1.2的方式定义.
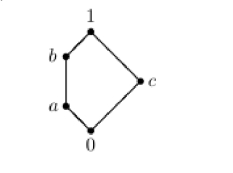
图1.2L上偏序“≤”的定义
则(L,≤)是格,但不是分配格.因为
![]()
一般地,分配格的子格是分配格.此外,在接下来将要介绍的格同态的作用下,分配格的像仍保持分配性.
定义1.3.12 设(L,≤)与(M,≤)是两个格(为简便计,我们这里用同一记号“≤”表示二者的偏序),f:L→M.如果对任意的a,b∈L都有
![]()
则称f为格同态(lattice homomorphism),简称f为同态(homomorphism).
如果同态f还是一个一一映射,则称f为格同构(lattice isomorphism),简称f为同构(isomorphism).此时称格(L,≤)与(M,≤)同构,记为(L,≤)≅(M,≤).
一般地,如果f:L→M是格同构,则其逆映射f-1:M→L也是格同构,因此格之间的同构关系是等价关系.(https://www.xing528.com)
注1.3.6 设(L,≤)与(M,≤)是两个有界格,如果f为格同态,则
![]()
下面,我们介绍序集的两类重要的的子集,即下集和上集,进而介绍两类特殊的下集和上集,即理想和滤子.
定义1.3.13 设(P,≤)是预序集,∅≠Q ⊆P.
(1)若Q满足条件:
![]()
则称Q是P的一个上集(up-set);
(2)若Q满足条件:
![]()
则称Q是P的一个下集(down-set).
给定预序集P的子集Q或元a∈P,可以按如下方式产生下集和上集:
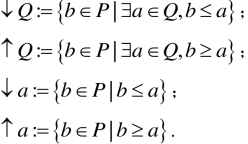
↑Q和↓Q分别称作由Q生成的上集和下集.由Q生成的上集和下集是是包含Q的最小上集和下集.称上集↑x和下集↓x为元x确定的主上集和主下集.本书行文中会谈到偏序集P的有限生成的上集或下集的术语,这里所谓的有限生成的上集(对应地,有限生成的下集)是指满足如下性质的上集(对应地,下集)R⊆P:存在非空有限子集Q⊆P使得↑Q =R (对应地,↓Q=R).
一般地,设P是预序集,其上集全体记为U(P),下集全体记为D(P),其中U和D分别取自上集和下集的英文首字母.如果在U(P)和D(P)上赋予集合包含关系⊆,则(U(P),⊆)和(D(P),⊆)都是偏序集.事实上,不难证明它们都是完备格.
定理1.3.6 设(P,≤)是预序集,x,y∈P,则下列条件等价:
(1)x≤y;
(2)↓x⊆↓y;
(3)∀Q∈D(P),y∈Q蕴涵x∈Q;
(4)↑y⊆↑x ;
(5)∀S∈U(P),x∈S蕴涵y∈S.
定义1.3.14 设(P,≤)是预序集,I⊆P且F⊆P.
(1)若I是非空下集,且是上定向的,即满足条件:
![]()
则称I是P的一个理想(idea);
(2)若F是非空上集,且是下定向的,即满足条件:
![]()
则称F是P的一个滤子(filter);
(3)若I(或F)是理想(或滤子)且I≠P(或F≠P),则称I(或F)是P的真理想(proper ideal)(或真滤子(proper filter)).
注1.3.7 设P是预序集,且P有最大元1和最小元0,则
(1)P的理想I是真理想当且仅当1∉I;
(2)P的滤子F是真滤子当且仅当0∉F;
(3)按照包含关系⊆,{0}和{1}分别是的P的最小理想和最小滤子.
注1.3.8 设P是预序集且a∈P,则↓a和↑a分别是P的理想和滤子,分别称之为由元a确定的主理想(principal ideal)和主滤子(principal filter).
当格是有界格时,我们容易证明存在简单的条件来分别判断下集和上集是否是理想和滤子.此外,理想和滤子都对集合的交运算具有封闭性.这些基本事实可以总结为如下定理:
定义1.3.15 设(L,∧,∨,0,1)是有界格,则下列结论成立:
(1)L的下集I是理想当且仅当对任意的a,b∈I有a∨b∈I;
(2)L的上集F是滤子当且仅当对任意的a,b∈F有a∧b∈F;
(3)L的任意多个理想(或滤子)组成的非空理想(或滤子)族的交集仍然是L的理想(或滤子).
本节最后,我们介绍素元的相关概念.
定义1.3.16 设(L,∧,∨)是格且a∈L.
(1)如果a≠1且对任意的x,y∈L而言,当x∧y=a时必有x=a或y=a成立,则称元a是L的交既约元(meet irreducible element);
(2)如果a≠1且对于任意的x,y∈L而言,当x∧y≤a时必有x≤a或y≤a成立,则称元a是L的素元(prime element);
(3)如果a≠0且对任意的x,y∈L而言,当x∨y=a时必有x=a或y=a成立,则称a是L的并素元(join prime element);
(4)如果a≠0且对任意的x,y∈L而言,当x∨y≥a时必有x≥a或y≥a成立,则称a是L的余素元(co-prime element).
定理1.3.7 设(L,∧,∨)是分配格且a∈L.则下列结论成立:
(1)a是L的素元当且仅当a是L的交既约元;
(2)a是L的余素元当且仅当a是L的并既约元.
证明 (1)设a是L的素元.任取x,y∈L,若x∧y=a,则除a≤x和a≤y成立以外,还有x∧y≤a也成立.利用a是L的素元这一假设可知x≤a或y≤a,所以由反对称性得x=a或y=a成立.
反之,设a是分配格L的交既约元.现取x,y∈L满足x∧y≤a.由分配律可得
![]()
因此由a是L的交既约元的假设直接可得a=a∨x或a=a∨y,从而x≤a或y≤a成立.
(2)可以如上对偶证明.
注1.3.9 由定理1.3.7的证明可知,一般地,格L的素元(或余素元)一定是交(或并)既约元,但反之不真.如例1.3.2中所给五元菱形格(d),元a,b和c都是交既约元,但都不是素元;同时,也容易看出元a,b和c都是并既约元,但也都不是余素元.
一般情况下,格的若干素元(或余素元)的下确界(或上确界)未必仍是素元(或余素元),但对于下定向(或上定向)的素元(或余素元)之集的下确界(或上确界)我们有如下结论:
定理1.3.8 设(L,∧,∨)是完备格,则下列结论成立:
(1)如果S是非空下定向的素元之集,则inf S是素元;
(2)如果T是非空上定向的余素元之集,则supT是余素元.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




