纳什均衡的定义，两人博弈的纳什均衡的计算

前面的分析与论述陈述了博弈树的表示方法及动态博弈的纳什均衡存在不可置信的威胁的问题。动态博弈用策略式描述的缺点一方面是在问题复杂时策略会很复杂，另一方面，策略式表达中求出的纳什均衡不能区分是否存在不可置信威胁的情况。本节我们讨论用博弈树直接分析纳什均衡的方法。

一、子博弈

子博弈，直观的含义是原博弈的一个部分，它本身也可以作为一个博弈进行分析，博弈树的一个子树所代表的博弈就是子博弈，子博弈的起始点是某个人选择行动的结点。包括这个结点及所有后续结及枝及终点结之后的收益，构成了一个子博弈树，这个子博弈树所代表的博弈称为子博弈。

需要注意，有时会出现博弈参与人不能判断自己到底处于哪个决策结的情况，这肯定是由于信息不完美的情况所造成的，这时这个结点及以下的部分形式上还是博弈树，但缺乏分析所需要的信息，因为起点不明确，无法分析。但现在我们主要对完美信息的讨论，不会出现这种情况，实际上，子博弈要求博弈已进行的信息能给定这个子博弈确切的起点与初始信息。

如图3.3中的博弈，在假设参与人1的行动可被观察时，有两个子博弈，如图3.5（a）的子博弈1与3.5（b）的子博弈2。

图3.5

实际上子博弈1存在着一个作为前提的信息：“参与人1选择了强竞争”，同理，子博弈2也有“参与人1选择了普通竞争”的初始信息。如果参与人2虽然后行动，但不能确定企业1选择了什么，这时图3.5（a）与3.5（b）不是子博弈，即使我们有这种信息：参与人1选择强竞争的概率是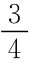，普竞争的概率是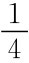，也不能构成子博弈。定义子博弈的目的是子博弈的分析能成为整体中的一部分，而起点不确定时，把图3.5（a）与3.5（b）分割出来考虑会失去意义。

一般而言原博弈也可以认为是一个子博弈。

二、子博弈精炼纳什均衡

引入了子博弈的概念后，再来分析图3.3中的博弈，（G2，J3）是它的纳什均衡，但可以注意到，这个策略组合在子博弈1（图3.5（a））中，参与人1的选择已经没有意义，但J3仍然可执行，在这一子博弈中，J3策略不是纳什均衡，因为根据策略，参与人2应选择强竞争，但选择普通竞争的收益是2，比强竞争－2的收益要高，所以不是子博弈1的纳什均衡，同理可以分析（G1，J4）也不是子博弈2的纳什均衡，而（G1，J2）在两个子博弈中却是纳什均衡。

这表明一个纳什均衡在各个子博弈中的意义可以反映这一纳什均衡的性质，因此，我们来讨论战略组合在子博弈中的表现问题，为此，我们规定：战略组合在子博弈中的意义是在子博弈初始信息的前提下，以战略组合的剩余部分在子博弈中的实施来考虑的，即子博弈的前提信息优先于战略路径。

如对（G2，J3），在子博弈1中的分析，子博弈的前提是参与人1选择了强竞争，而（G2，J3）的战略路径不会出现在这个结点。按优先原则，以参与人1选择强竞争作为前提，（G2，J3）在子博弈中剩余部分的实施就是参与人2的行动选择，按照这个约定，可定义子博弈精炼纳什均衡。

定义3.3.1 博弈的战略组合s＊＝（s＊1，s＊2，…，s＊n）是一个子博弈精炼纳什均衡，如果满足以下两个条件：

（1）它是原博弈的纳什均衡；

（2）它在每一个子博弈上也构成纳什均衡。

按此定义，图3.3的博弈中，（G1，J2）是子博弈精炼纳什均衡，因为在子博弈1与子博弈2中实施J2都是最优的，而（G2，J3）就不是子博弈精炼纳什均衡。

可以注意到，博弈真实进行所展示出来的路径并不能反映战略组合的全部信息，而战略组合在所有的子博弈中的路径，才能完整的反映出战略组合的全貌。子博弈精炼纳什均衡是在所有子博弈中均能给出纳什均衡的行动选择规则，所以，我们可以通过子博弈中的最优路径来概括出子博弈精炼纳什均衡的战略的文字描述。

一个子博弈精炼纳什均衡，不会有后行动者不可置信的威胁存在。(www.xing528.com)

下面介绍求子博弈精炼纳什均衡的实用方法——逆向归纳法。

三、逆向归纳法

逆向归纳法的思路是从博弈的最后阶段开始，分析最后阶段所有子博弈的纳什均衡。由于最后阶段只有一次行动，容易求出最优的行动，原博弈的子博弈精炼纳什均衡的路径必然包含其中的一个子博弈的最优解，但不知是哪个子博弈的枝。但这样做了以后可以对原博弈作这样的等效处理：保留多个子博弈的最优解，去掉所有其他枝，这样，终点结与最后阶段的决策结之间就只保留了一条连线，把最后阶段的子博弈的起始结作为终结点，并保留最优枝的收益作为收益，这样做后，博弈减少了一个阶段，但我们已记录了最后阶段的最优决策，这样处理后的博弈与原博弈等效。依此类推，对等效处理后的博弈再重复一次上述过程，如此反复，可以得到子博弈精炼纳什均衡在所有子博弈上的路径。

下面用图3.6的数字例子来说明逆向归纳法的求解。

图3.6 说明逆向归纳法的例

图3.6中有三个最下级的子博弈，分别表示在虚线的框内，可以把最优行动对应的枝加粗，以示是最优策略，分别是三个虚线框内的三条粗线。这样做后博弈等价于图3.7的博弈，又有图3.7的虚线框中的子博弈，参与人2的最优行动是选择U，这样又可得图3.8的简化。

图3.7 图3.6的等效形式

图3.8 图3.7的等效形式

图3.8中参与人先行动时选择M是最优策略，这样就求出了子博弈纳什均衡的均衡路径是“参与人1选择M，参与人2接着选U，参与人1再行动时选T”。

当然上面是为了描述过程而作了分解，解题时可以采用更简单的记号来记录逆向归纳法的求解过程。

对最下层的决策结求最优，并把最优的支线加粗。而把这一枝下的收益写到决策结边上，写上收益的决策结相当于终结点。再对上一层的决策结重复上述过程，一直到起始结。如图3.9，粗线及粗线的连线是子博弈纳什均衡的均衡路径。理性博弈人博弈时可观察到的是

参与人1得到3，参与人2得到2，两条粗线条不出现在均衡路径中。但它们是子博弈精炼均衡的有机组成部分。

图3.9 求解过程描述

用文字表示其均衡策略是：

参与人1：“先行动时将选择M，有再行动机会时如果对方选U则选T，如果对方选D则选R。”

参与人2：“如果对方选M，就选U，如果对方选择了L就选D。”

我们把纳什均衡策略实施形成的博弈过程中可观察到的路径称为均衡路径，它是从起点到某个终点的一条链，在图3.9的博弈中，参与人选M，参与人2选U，参与人1再选择时选T就是子博弈精炼纳什均衡的路径。