如上所述,内力是外力作用使构件内部相连部分之间相互作用力的改变量,并沿截面连续分布。为了描述内力的分布情况,现引入内力分布集度即应力的概念。
1.正应力与切应力
如图1-10(a)所示,在截面m-m上任一点k的周围取一微小面积ΔA,并设作用在该面积上的内力为ΔF,则ΔF与ΔA的比值称为ΔA内的平均应力,并用pm表示,即
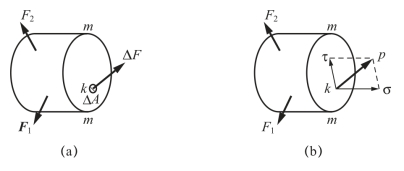
图1-10 截面上一点处的平均应力与应力的概念

一般情况下,内力并非沿截面均匀分布,平均应力的大小及方向将随所取面积ΔA的大小不同而不同。为了更精确地描写内力的分布情况,应使ΔA趋于零,由此所得平均应力的极限值称为截面m-m上k点处的应力或全应力,并用p表示,即

显然,应力p的方向即ΔF的极限方向。为了分析方便,通常将应力p沿截面法向与切向分解为两个分量[图1-10(b)]。沿截面法向的应力分量称为正应力,并用σ表示;沿截面切向的应力分量称为切应力,并用τ表示。显然有
![]()
在我国法定计量单位中,力与面积的基本单位分别为N与m2,应力的单位为Pa[帕(斯卡)],1Pa=1N/m2。在材料力学中,应力的常用单位为Mpa(兆帕),其值为
![]()
由式(1-5)可知,如果力的单位用N,长度的单位用mm,则得到的应力单位就是Mpa,不必再转换单位,这为数值计算带来方便。
2.单向应力、纯剪切与切应力互等定理
如前所述,受力构件中一点的应力不仅与该点的空间位置有关,而且与该点所在的截面有关。由于过一点可以截出无穷多个截面,所以一点的应力状态实际上有无穷多个。构件中一点在所有截面上应力的集合称为该点的应力状态。研究表明,只要知道一点在一些特定截面上的应力,其他任意截面上的应力都可以通过计算得到。
图1-11(a)所示的直角坐标系(x,y,z),为考察构件中任意一点k处的应力状态,选取过k点的三个特殊截面,它们的外法线分别与x轴、y轴和z轴的标准单位矢量i、j、k的正向相同,可称为正x面、正y面和正z面。若三个特殊截面上的应力矢量分别为px、py和pz,将px、py和pz分别在x轴、y轴和z轴上分解,得到图1-11(b)所示的9个应力分量:σxx、τxy、τxz;σyy,τyx,τyz;σzz,τzx,τzy。其中,第一个下标表示截面的法线方向,第二个下标表示该应力的方向。为了简洁,通常将σxx、σyy和σzz分别写为σx、σy和σz。
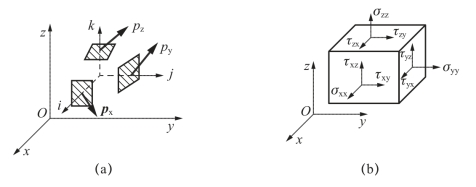
图1-11 截面上一点处应力的标记方法
图1-11(b)中是将三个特殊截面(即正x面、正y面和正z面)再加上三个负面,即负x面(外法线与x轴负向相同的面)、负y面(外法线与y轴负向相同的面)、负z面(外法线与z轴负向相同的面),围合成一个正六面体,可以理解为是从构件中截出的包含k点的单元体,该单元体表面上的应力就代表k点的应力状态。图1-11(b)给出的是最复杂的应力情况,9个应力分量全不为零。而在材料力学研究的问题中,往往只有2个应力分量不为零,其余应力分量均为零,所以要简单得多。
单元体受力最基本、最简单的状态有两种:一种是单向受力或单向应力状态,如图1-12(a)所示;另一种是纯剪切状态,如图1-12(b)所示。在单向应力状态下,单元体只在一对互相平行的截面上承受正应力,当σ为拉应力时,称为单向拉伸应力状态;当σ为压应力时,称为单向压缩应力状态。纯剪切应力状态只承受切应力的作用。
切应力具有独特的性质。图1-13(a)中,设单元体的三个边长分别为dx、dy和dz,并假设单元体顶面和底面的切应力为τ,左、右侧面上的切应力为τ′。根据静力平衡关系,有(https://www.xing528.com)

图1-12 两种典型应力状态
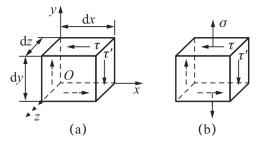
图1-13 切应力互等的证明图
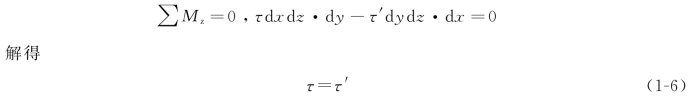
式(1-6)表明,在单元体互相垂直的截面上,垂直于截面交线方向的切应力大小相等,方向均指向或离开该交线。这种关系称为切应力互等定理。即使截面上存在正应力[图1-13(b)],切应力互等定理仍然成立,因为存在的正应力对z轴之矩的代数和为零。
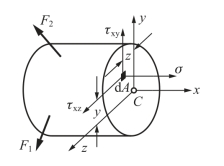
图1-14 应力及其与内力分量之间的关系
3.应力与内力分量之间的关系
应力作为截面上分布内力在一点的集度,与截面的内力分量之间有着密切的关系。为了得到这种关系,依据横截面及其形心C建立图1-14坐标系Cxyz,并考察作用在横截面的微元面积dA上的正应力σ和切应力τxy、τxz,将它们分别乘以微元面积,即可得到作用在微元面积dA上的微内力σdA、τxydA和τxzdA。将这些微内力分别对Cxyz坐标系中的x、y和z轴投影及取矩,再沿整个横截面积分,即可得到应力与上述6个内力分量之间的关系式:
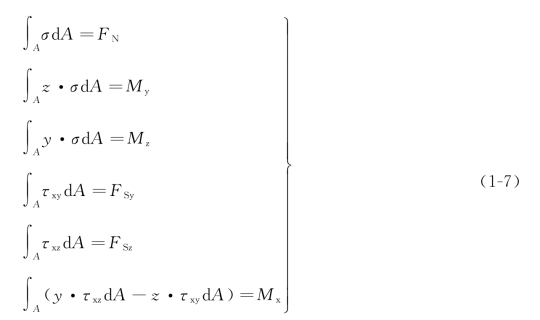
式(1-7)是构件在任意荷载作用下应力与内力均应满足的一般关系。在对构件基本变形的讨论中,必须满足这些关系,这是获得相关应力计算公式的依据。
【例1-1】 如图1-15所示,圆截面杆件的直径为d,其横截面上的正应力在图示坐标系下的分布规律为σ=A0rcosθ+B0rsinθ+C0,试求该截面上的内力分量与常数A0、B0、C0之间的关系。
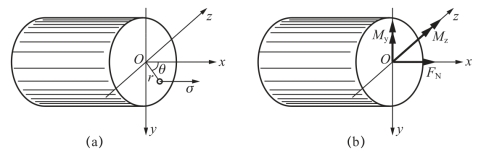
图1-15 截面上的应力和应力分量
解:由于截面上正应力沿x轴方向,故在y、z轴上的投影为零,对x轴的矩也为零,即

根据式(1-7),并用坐标变换:y=rcosθ,z=rsinθ,dA=rdrdθ,则有

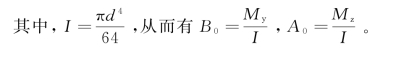
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




