稀疏光流算法简介

孔径问题的产生是由于方程个数小于变量个数，从而使得光流约束方程有无穷多个解。解决这一问题的一种方式是：强行使得方程个数多于变量个数，然后对方程进行求解。具体应该怎么做呢？我们不妨令：图像中的某一个小区域内的所有像素点具有相同的速度。于是，对于图像区域内的每一个像素点，都有一个光流约束方程。我们可以尝试通过多个光流约束方程，来求解图像小区域的运动速度。

上述过程中，我们先对图像进行了离散化处理，然后，通过增加约束条件：图像小区域内的所有像素点具有相同速度，来求解光流约束方程组。求解过程也就是相应的算法。

11.3.1　一个具体例子

首先，我们通过一个具体例子，来理解稀疏光流算法的实现过程。对于图11.7中的两个图像小块，每一个像素点的运动都是一致的，我们要设法求出图像小块的整体运动速度。

对于每一个像素点，都可以计算一组{Ex,Ey,Et}，然后，用所求得的多组{Ex,Ey,Et}数据来共同求解光流约束方程(11.5)。在此之前，我们还有一个细节问题需要解决，如何计算数据{Ex,Ey,Et}？如果我们直接采用一阶差分格式来计算各个像素点的{Ex,Ey,Et}，那么，所得到的结果中，Ex、Ey和Et的总个数是不一致的。对于图11.7中的情况，所有的Ex会形成一个5×4的矩阵，所有的Ey会形成一个4×5的矩阵，而所有的Et会形成一个5×5的矩阵。

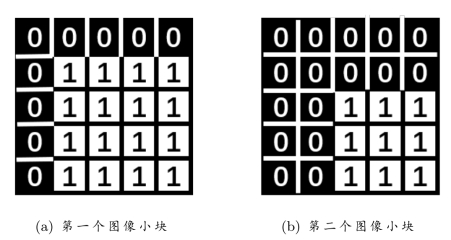
图11.7　对于图中的两个图像小块，每一个像素点的运动都是一致的，我们要设法求出图像小块的整体运动速度。

为了解决这一问题，我们需要合理地设计一阶差分格式，对同一个像素点（或格栅点）的{Ex,Ey,Et}进行估计。我们可以采用图11.8所示的差分格式，来进行近似计算。在图11.8中，指标i、j和k分别对应于：x、y和t的离散量，我们可以用如下形式

来估计一阶偏微分。计算过程中，我们用到了该像素点附近邻域内的像素点的亮度值。注意，这里的“附近领域”是针对视频而言的，也就是说，我们所考虑的是：视频中邻接的两张图像。

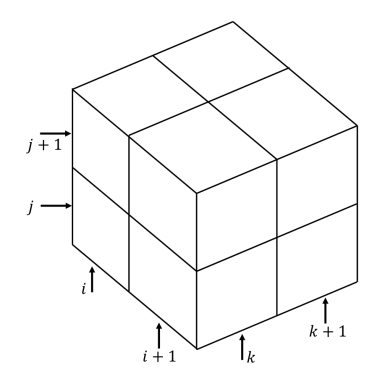
图11.8　我们可以使用：2×2×2的立方体中的亮度值的一阶差分，来近似估计：迭代方法中所需要的一阶导数。我们使用：空间上连接在一起的四个图像单元（像素点）在相邻的两帧图像中的亮度值，来形成这个2×2×2的立方体。

通过计算，我们最终得到了3个“尺寸一样”的数据矩阵：

对于图11.7中的两个图像小块，相应地，

式(11.5)所对应的一组光流约束方程为：

其中0为一个4×4的全零矩阵。上式中包含16个方程，只含有2个未知数u和v，因此，有望对其进行求解。

进一步，我们可以将式(11.16)整理为线性方程组

的形式，其中x=(u,v)T，A=(a1,a2)的两个列向量分别为：(www.xing528.com)

也就是说，分别将E x和E y按列“拼接”成两个列向量。相应地，

也就是说，将E t按列“拼接”成一个列向量。

求解(11.17)是一个众所周知的结论[2]，即：

又称为方程组(11.17)的最小二乘解。

对于图11.7中的两个图像小块，

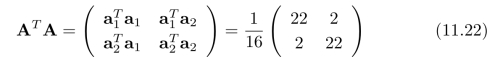
以及，

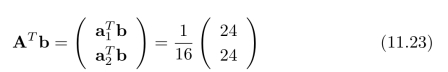
最终，我们求得：

这与我们对图11.7中的图像小块运动情况的“观测”结果是一致的。

11.3.2　算法实现过程

稀疏光流法的算法实现过程似乎是直接的。我们只需要将图像分割成许多小块，然后，通过上一小节中介绍的方法，直接进行求解即可。但是，我们还有一个细节问题需要处理。式(11.21)中的最小二乘解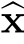 x并不一定存在。当且仅当(A T A)-1存在时，我们才能求解 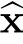x。于是，我们的问题转化为了：矩阵A T A可逆（或“鲁棒”可逆）的条件是什么？

事实上，我们对于矩阵A（和A T A）并不陌生，在第10章10.5小节中，矩阵A被用于进行角点检测。因此，我们得到如下结论：

•当且仅当图像块中包含角点时，才可以通过式11.21来有效估计图像小块的（整体）运动速度。

这也意味着稀疏光流法的算法实现过程包括如下两步：

1.角点检测：将图像划分为若干小块，然后，逐一判断每一个小块中是否包含角点（参见第10章10.5小节的内容）。

2.计算光流：对于包含角点的小块，直接通过式(11.21)计算光流，即：图像小块的平均速度。

这与我们的直观感受是一致的。图像中，只有角点的运动信息是可以被精确感知的，参见10.7小节的内容。稀疏光流法直接估计角点的运动信息，因此，又被称为角点流。