随机事件的自信息和条件自信息优化为：探究随机事件的自信息及条件自信息

1.随机事件的不确定度

通过某个过程或手段，获得了关于随机信源一定的了解，减小了不确定度，也就是从这个信源获得了信息。从信源获取信息的过程就是其不确定度缩减的过程。可见信源包含的信息与其不确定度是紧密相关的。

在统计分析中，使用概率作为衡量不确定度的一种指标。可以推断信源产生的随机事件所包含的信息应该是其概率的函数。下面通过例子说明随机事件的不确定度与概率之间的必然联系。

【例2.5】

有4个布袋，每个布袋中装100个对人手感觉完全一样的不同颜色的球。其中，

a布袋：装红球99个，白球1个；

b布袋：装红球50个，白球50个；

c布袋：装4种颜色的球，红、白、蓝、黑各25个；

d布袋：仅装红球100个。

从这4个布袋中分别取出1个球，猜测从4个布袋中取到球的颜色的难度？

解a布袋：可以确定这样的信源发出的消息具有不确定度，因为取出一个球可能是红球，也可能是白球。但很容易猜测出它大概是红球（猜测正确率为99%），因为红球多，所以猜测的难度不大，当然不确定度也不大。

b布袋：猜测从布袋中随意取出一个球的颜色的难度比a布袋大。因为此时红球和白球一样多，不容易猜测（猜测正确率为50%），所以这种情况下信源发出的消息的不确定度较大。

c布袋：猜测从布袋中随意取出一个球的颜色的难度更大，因为这时更难猜测（猜测正确率为25%），所以这种情况下的不确定度更大。

d布袋：布袋中仅有100个红球，取出的一个球必是红球，是确定性事件，猜测难度没有了。

由例2.5可知，事件发生的不确定度与事件发生的概率有关。一般情况下，一个信源可以用一个概率空间（如式（2.1））来描述，而信源的不确定度可以用这个概率空间的可能状态数目及其概率来描述。

【例2.6】（续例2.5）

设“取出红球”事件记为a₁，“取出白球”事件记为a₂，“取出蓝球”事件记为a₃，“取出黑球”事件记为a₄，则4个布袋的概率空间可以表示为

a布袋：取出的可能是红球，也可能是白球，其概率空间为

b布袋：取出的可能是红球，也可能是白球，两种球的数量相同，其概率空间为

c布袋：取出的可能是红球、白球、蓝球和黑球，4种球的数量相同，其概率空间为

d布袋：只能取出红球，不可能是白球、蓝球或黑球，其概率空间为

从上面的分析，可以得出有关不确定度的重要结论如下：

1）信源的不确定度与其概率空间的消息数及其概率分布有关。事件发生的概率越大，不确定度就越小；而事件发生的概率越小，不确定度就越大；对于发生概率等于1的必然事件，则不存在不确定度。

2）在信源消息数一定时，信源消息等概率分布时的不确定度最大。

3）在信源消息等概率分布时，不确定度与信源概率空间的可能状态数或相应的概率有关，状态数越多或相应的概率越小，不确定度越大。

不确定度越大，越难猜测。根据例2.5和例2.6，可以容易写出下列表示信源的不确定度大小的不等式：

0=布袋d＜布袋a＜布袋b＜布袋c＜∞

2.自信息的定义与含义

某随机事件x发生所含的信息量应该是该事件发生的先验概率P（x）的函数，即

I（x）=f[P（x）] （2.9）

称I（x）为事件x发生所含的自信息（也称为自信息量）。

I（x）应该满足以下条件：

1）I（x）=f[P（x）]是关于P（x）的单调递减连续函数，概率小的事件一旦发生则赋予的信息量大，概率大的事件发生则赋予的信息量小。

2）信息量具有可加性，即两个独立事件的联合自信息量应该等于各事件自信息量之和。

3）当P（x）=1时，I（x）=0，表示确定事件发生得不到任何信息。

4）当P（x）=0时，I（x）→∞，表示不可能事件一旦发生，信息量将无穷大。

综合上述条件，数学上可以严格证明，对数函数是满足上述要求的唯一函数形式。为此，给出自信息量和联合自信息量的定义如下：

定义2.1 在离散随机变量X中，事件x（x∈X）的自信息（或自信息量）I（x）定义为该事件发生概率P（x）的对数的负值，即

定义2.2 在离散联合随机变量集XY上，联合事件xy（xy∈XY）的联合自信息（或联合自信息量）I（x，y）定义为该事件发生概率P（xy）的对数的负值，即

信息量的单位取决于对数所选取的底。由于P（x）是小于等于1的正数，又根据实际情况自信息I（x）也必然是非负数，所以对数的底应该选为大于1的任意数。

1）取以2为底的对数，其信息量单位称为比特（bit，binary unit的缩写），即

I（x）=-log₂P（x）bit

2）取以e为底的自然对数，其信息量单位称为奈特（Nat，Nature unit的缩写），即

I（x）=-lnP（x）Nat

3）取以10为底的对数，其信息量单位称为哈特（Hart，Hartley的缩写，以纪念哈特莱首先提出用对数来度量信息），即

I（x）=-lgP（x）Hart

4）一般情况，如果取以m（m＞1）为底的对数，则

I（x）=-log_mP（x）m元单位

根据对数换底关系式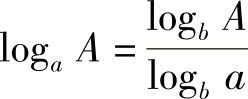，有

1 Nat=log₂e≈1.443bit

1 Hart=log₂10≈3.322bit

1 bit=ln2≈0.693Nat

1 bit=lg2≈0.301Hart以后，常采用以2为底的对数，且为了书写简洁把底数“2”略去不写，即用log表示log₂。

自信息量的含义可以从多个不同的角度来理解：(www.xing528.com)

1）自信息量I（x）表示了事件x是否发生的不确定度的大小。一旦该事件发生，就消除了这种不确定度，带来了信息量。

2）自信息量I（x）表示了事件x的发生所带来的（或所提供的）信息量的大小。

3）自信息量I（x）表示了确定事件x是否发生，所需要的信息量的大小。

4）如果用二元数据将这些自信息量表示出来，自信息量（以“bit”为单位）I（x）表示了所需要的位数。

在无噪信道中，事件发生以后，能正确无误地传输到收信者，所以自信息量就等于收信者接收到事件后所获得的信息量。这是因为消除了自信息量I（x）大小的不确定度才获得了这么大小的信息量。

【例2.7】

“小丽今天吃饭了”事件发生的概率是99.99%，“某沿海地区发生海啸”事件发生的概率是0.01%，分别求这两个事件的自信息量。

解 设“小丽今天吃饭了”事件记为a，“某沿海地区发生海啸”事件记为b，则P（a）=0.9999，P（b）=0.0001，因此

I（a）=-log P（a）=-log 0.9999=0.0001423 bit

I（b）=-log P（b）=-log 0.0001=13.29 bit

由例2.7知，事件b的发生带来的信息量远大于事件a的发生带来的信息量，这也就印证了为什么看到海啸发生会非常吃惊，而看到某人吃饭并不会留下什么印象。这是因为一日三餐是人类生存的正常行为，而某地区发生海啸则是极不寻常的事情。

【例2.8】

对于二元数字序列，假设每码元的出现完全随机且等概率，则每码元的自信息量为

对于2ⁿ元数字序列，假设每码元的出现完全随机且等概率，则每码元的自信息量为

可见，2ⁿ元数字序列每码元携带的信息量是二元数字序列每码元携带的信息量的n倍。

因-log（1/2）=1 bit，所以1 bit信息量就是两个互不相容的等可能事件之一发生时所提供的信息量。

注：这里“bit”是指抽象的信息量单位。与计算机术语中二元数字（binary digits）的“bit”含义不同。这两种定义之间的关系是每个二元数字所能提供的最大平均信息量为1 bit。

【例2.9】

有12个形状相同的球，其中一个球的重量与其他球不同（不知是重还是轻），其他球均等重。为了用天平（无砝码）称出这个不同重量的球，问至少需要称多少次？

解 在12个形状完全相同的球中，哪一个球的重量与其他球不同（不知是重还是轻）都是“不确定的”。用天平（无砝码）比较左右两边轻重的测量方法来称出这个不同重量的球，每测一次可以获得一定的信息量，能消除部分不确定度。测量若干次后，能消除全部不确定度，获得全部信息，此时就可以确定出其中一个不同重量的球。

设“在12个形状相同的球中某球为重量不同的球”为事件a，其出现的概率为P（a）=1/12。设“重量不同的球比其他球的重量是重或轻”为事件b，其出现的概率为P（b）=1/2。则事件a和b的自信息量分别为

I（a）=-log P（a）=log 12

I（b）=-log P（b）=log 2要找出这个不同重量的球（不知是重还是轻）所需的信息量是消除这两个事件的自信息量。由于这两个事件是统计独立的，所以所需的信息量为I（a）+I（b）=log 24。而天平称一次能判断出“重”“轻”和“相等”3种情况，其出现概率为1/3，于是天平测一次能获得的信息量为log 3，至少需要称的次数为

因此，至少称重3次才能从12个球中找出重量不同的那一个球。

需要指出的是，例2.9的计算结果仅是从信息量的角度论证了用天平称3次就可以找出重量不同的球，但没有给出具体的称量方法。对于此类问题，通过信息量得到的结论只说明问题可能有解，违背该结论的方法则一定无解。

3.条件自信息的定义与含义

定义2.3 在离散联合随机变量集XY上，在事件y（y∈Y）给定条件下，发生事件x（x∈X）的条件自信息（或条件自信息量）I（x|y）定义为该条件事件发生概率P（x|y）的对数的负值，即

约定“在事件y（y∈Y）给定条件下，发生事件x（x∈X）”的条件事件记为x|y。条件自信息量的含义也可以从多个不同的角度来理解：

1）条件自信息量I（x|y）表示了条件事件x|y是否发生的不确定度的大小。一旦该事件发生，就消除了这种不确定度，带来了信息量。

2）条件自信息量I（x|y）表示了条件事件x|y的发生所带来的（或所提供的）信息量的大小。

3）条件自信息量I（x|y）表示了确定条件事件x|y是否发生，所需要的信息量的大小。

4）如果用二元数据将这些条件自信息量表示出来，条件自信息量（以“bit”为单位）I（x|y）表示了所需要的位数。

容易证明（性质的证明留作习题），自信息量、条件自信息量和联合自信息量之间有如下关系：

性质2.1（强可加性） I（x，y）=I（x）+I（y|x）=I（y）+I（x|y）。

性质2.2（可加性） 当随机变量X与Y相互独立时，I（x，y）=I（x）+I（y）。

【例2.10】

英文字母中“h”出现的概率为P（h）=0.0467，“t”出现的概率为P（t）=0.0796，且实际英文中字母的出现是相关的，统计知字母组合“th”和“ht”出现的概率分别为P（th）=0.0321，P（ht）=0.0013。计算下列问题：

1）英文字母“h”和“t”的自信息量。

2）假定前后字母出现是相互独立的，计算字母组合“th”和“ht”的联合自信息量。

3）计算实际英文中字母组合“th”和“ht”的联合自信息量。

4）计算实际英文中出现字母“t”后再出现字母“h”的条件自信息量，以及出现字母“h”后再出现字母“t”的条件自信息量。

解1）英文字母“h”和“t”的自信息量为

I（h）=-log P（h）=-log 0.0467=4.420 bit

I（t）=-log P（t）=-log 0.0796=3.651 bit

2）当字母的出现相互独立时，字母组合“th”和“ht”的联合自信息量为

I（t，h）=I（h，t）=-log P（t）P（h）=-log P（t）-log P（h）=8.071 bit

3）实际英文中字母组合“th”和“ht”的联合自信息量为

I（t，h）=-log P（th）=-log 0.0321=4.961 bit

I（h，t）=-log P（ht）=-log 0.0013=9.587 bit

4）根据公式P（xy）=P（x）P（y|x）分别计算条件概率

则出现字母“t”以后，再出现字母“h”的条件自信息量为

而出现字母“h”以后，再出现字母“t”的条件自信息量为