连续系统的特性与应用

以如图5-2所示的简支梁代表的弯曲变形系统为例进行说明。当系统按照某一阶频率ω 做主振动时，系统的位移响应可表示为

式中：y（x）为描述各截面振幅的连续函数，也代表了该阶主振型函数（它们之间只相差非零常数倍）。

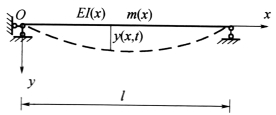
图5-2

系统的动能及其最大值（在系统的静平衡位置出现）分别为

根据材料力学的结论，梁的应变能也就是系统的势能为

势能的最大值（在系统的最大位移处出现）为

在不计阻尼时，有T（t）+U（t）=Tmax+0=0+Umax，将动能和应变能的最大值代入此式可得到

这就是连续系统的瑞利商的表达式，其分子为该阶主振型的主刚度，分母则为该阶主振型的主质量。对于其他变形形式（纵向振动、扭转振动等）的连续系统，按照上述的能量守恒关系可得到与此式类似的瑞利商表达式。

当所选的y（x）正好是第一主振型函数时，可求得第一阶频率的精确值，若正好是第二主振型函数，则可求出第二阶频率的精确值，以此类推。但问题是往往不能预知实际的振型函数，所以瑞利法计算的固有频率的精度完全依赖于所假设的振型函数y（x）。一般只能给出与第一振型函数接近的试函数，因此瑞利法一般用于估算基频。下面就如何选取第一主振型假设函数，提出以下几点原则。

（1）试函数y（x）的选取，至少要满足位移边界条件，否则误差会太大。为了尽量接近实际的第一振型函数，最好还能满足力的边界条件。

（2）从例5-1的情况，以及第3章、第4章中的诸多例题可见，多自由度系统或连续系统的第一主振型与重力作用下的静变形比较接近。通常选取重力作用下的静变形为假设的第一主振型。对连续系统而言，它既满足系统的位移边界条件，又满足系统的力的边界条件。按照功能原理，此时系统势能的最大值等于重力所做的功，即

(www.xing528.com)

式中：y（x）为重力作用下的静挠曲线。

于是式（5-25）变为

（3）工程上常会遇到以下几种情况，其施加重力的方法是：对于图5-3（a）所示的竖向悬臂结构，主要产生水平方向的弯曲振动，分布重力应水平向施加；对于图5-3（b）所示的两跨连续梁，与第一主振型相接近的挠曲线应是两跨方向相反，分布重力必须反向施加；对于图5-3（c）所示的刚架，若求其对称的振动频率，应施加图示的竖向重力。但这类结构的第一振型一般是水平方向的，故要求基频的话，应使重力荷载沿水平方向施加，而为了计算静挠曲线方便，可仅在横梁上施加水平集中重力。

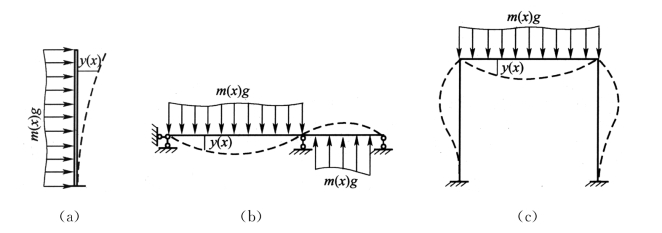
图5-3

（4）在许多实际问题中，一些杆件上有若干集中质量，且系统中有弹簧支承和弹性固定端。若某一振动系统，在x=xi处有集中质量Mi，在x=xj处有弹簧支承kj，在x=xn处有弹性固定端支承kθn，此时系统的最大动能和最大势能分别为

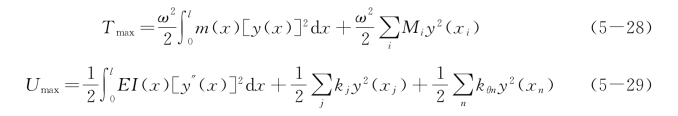
故

式（5-30）的分子和分母分别为第4章振型函数正交性中，非齐次边界条件下的主刚度和主质量。

如前所述，上式中y（x）的选取可近似地用分布重力或集中重力作用下的挠曲线，或采用分布重力与集中重力共同作用下的挠曲线，但由于存在弹性支承，其计算比较烦琐。一般地也可根据经验近似选择y（x），此时由于考虑了弹性支承的势能，没必要再考虑弹性支承处的位移边界条件。

当杆件系统中无弹性支承时，若采用集中重力和分布重力共同作用下的挠曲线，将最大势能用重力的功来代替，则式（5-30）成为

当无分布质量时，式（5-31）可进一步简化为

这就是用瑞利法计算多自由度系统基频近似值的第三种表达式（前两种表达式即为第一和第二瑞利商）。

与多自由度系统的情况类似，用瑞利法得到的连续系统基频的估算值，与精确解相比将偏大。