数据处理方法：从测量结果到精准结论

在同一条件下，对某一量进行n次重复测量获得测量列x1，x2，…，xn。在这些测得值中，可能同时含有系统误差、随机误差和粗大误差。为获得可靠的测量结果，对测量列的各项误差分析和处理，消除或减小测量误差的影响，提高测量精度。

3.5.5.1　测量列中随机误差的处理

随机误差是客观存在不可避免和无法消除的。为了正确评定随机误差，可用概率论与数据统计的方法对测量列进行处理，估算随机误差的数值和分布规律，确定测量结果。在假定测量列中不存在系统误差和粗大误差的前提下，可按下列步骤对随机误差进行处理。

（1）计算测量列的算术平均值。

当测量列中没有系统误差时，若测量次数无限增加，则算术平均值必然等于真值。在进行有限次测量时，算术平均值最接近真值 x0。当测量列中没有系统误差和粗大误差时，一般取测算术平均值作为测量结果。实际上算术平均值只能近似地等于真值。

（2）计算残差 vi。

测得值 xi与算术平均值之差称为残余误差（简称残差）vi，即

①残差的代数和等于零，即=0。这个特性可校核算术平均值及残差计算的准确性。

②残差的平方和最小，即=min。用算术平均值作为测量结果最可靠、最合理。

（3）计算标准偏差（测量列中单次测量值的标准偏差）。

实际测量时常用残差 vi代表 δi，用算术平均值x代替真值x0，按贝赛尔公式得出测量列中单次测量值（任一测得值）的标准偏差σ 的估算值为

由式（3.14）计算出值后，便可确定任一测得值的测量结果。若只考虑随机误差，则单次测量的测量结果可表示为

式中，xi为某次测得值。

例如，某次测量的测得值为50.003 mm，若已知标准偏差σ＝0.000 7 mm，可信度取99.73%，则该测得值的测量极限误差为±3×0.000 7 mm＝0.002 1 mm。测量结果为

50.003 mm±3×0.000 7 mm＝50.003 mm±0.002 1 mm

上述结果说明，该测得值的真值有99.73%的可能性在50.000 9～50.005 l mm范围内，可写作（50.003±0.002 1）mm。

（4）计算测量列算术平均值的标准偏差。

如果在等精度条件下对同一被测几何量进行m组（每组n次）等精度测量，则对应每组n次测量都有一个算术平均值，每组算术平均值也不一定相同。它们分布范围一定比单次测得值的分布范围要小得多。根据误差理论，测量列算术平均值的标准偏差与测量列单次测得值的标准偏差，存在如下关系：

由式（3.16）可知，在一定的测量条件下（即σ 一定），重复测量n次得到的算术平值的标准偏差是单次测量的σ 的。多次测量结果的精度比单次测量的精度高，增加测量重复次数，可提高测量的精度。但是，n也不能无限大，σ 一定时，当n＞10以后，再增加重复测量次数，σx减小已很缓慢，对提高测量精度效果不大，而且随着测量次数的增多，恒定的测量条件越难保证，最终将产生新的误差。因此，一般取n＝10～15。

（5）计算测量列算术平均值的极限误差。

若按正态分布，则算术平均值测量极限误差为

多次测量的测量结果可表示为

3.5.5.2　测量列中系统误差的处理

系统误差的大小表明测量结果的准确度。系统误差越小，则测量结果的准确度就越高。揭示系统误差出现的规律，消除系统误差对测量结果的影响，是提高测量精度的有效措施。

（1）发现系统误差的方法。

①实验对比法。为了发现存在的定值误差，可采用实验对比法，即通过改变测量条件来发现误差。在误差分布曲线图上，常值系统误差不改变测量误差分布曲线的形状，只改变测量误差分布中心的位置。从测量列的原始数据本身看不出是否存在常值系统误差。但如果改变测量条件，对同一被测量进行等精度重复测量，若前后两次测量列的值有明显差异，则表示有常值系统误差存在。例如，用比较仪测量某一线性尺寸时，若按“级”使用量块进行测量，其结果必定存在常值系统误差，该常值系统误差只有用级别更高的量块进行测量对比才能发现。

②残差观察法。变值系统误差不仅改变测量误差分布曲线的形状，而且改变测量误差分布中心的位置。揭示变值系统误差，可使用残差观察法。据测量列的各个残差大小和符号的变化规律，直接由残差数据或残差曲线图形来判断有无系统误差，如图3.13所示。

图3.13　变值系统误差的发现

若残差大体上呈正负相间出现且无规律性变化，则不存在变值系统误差，如图3.13（a）所示；若残差按近似的线性规律递增或递减，则可判定存在线性变值系统误差，如图3.13（b）所示；若残差的大小和符号呈规律性周期变化，则可判定存在周期性变值系统误差，如图3.13（c）所示。当然这种方法不能发现定值系统误差。

这种观察法要求有足够的连续测量次数，否则规律不明显，会降低判断的可靠性。

（2）消除系统误差的方法。

①从产生根源上消除系统误差。在测量前对采用的测量原理、方法、计量器具、标准器以及定位方式、计算方法、环境条件等各个环节进行分析检查，排除可能引起系统误差的因素。

②用修正法消除系统误差。若发现系统误差的存在，且知道其大小和正负号，则可采用修正的方法加以消除或减小。这种方法可消除定值系统误差。

③用抵消法消除定值系统误差。这种方法要求在对称位置上分别测量一次。以使这两次测量数据所含的系统误差大小相等，符号相反。取这两次测量数据的平均值作为测得值，即可抵消其定值系统误差。例如，在工具显微镜上测量螺纹螺距以及牙型半角时，为了消除被测螺纹轴心线与仪器的纵向导轨不平行而引起的系统误差，可分别测量左右牙侧的螺距，然后取平均值作为测得值，则可抵消测量时因安装不正确（被测螺纹轴心线与仪器的纵向导轨不平行）引起的大小相同、符号相反的系统误差。

④用半周期法消除周期性系统误差。对周期性系统误差，可以每相隔半个周期进行一次测量，以相邻两次测量数据的平均值作为一个测得值，即可有效消除周期性系统误差。

消除和减小系统误差的关键是找出误差产生的根源和规律，系统误差不可能完全消除。一般来说，系统误差若能减小到使其影响值相当于随机误差的程度，便可认为已经被消除。

3.5.5.3　测量列中粗大误差的处理

粗大误差的数值（绝对值）相当大，会对测量结果产生明显的歪曲，在测量中应尽可能避免。如果粗大误差已经产生，则应根据判断粗大误差的准则将其从测量列中剔除。粗大误差的判断准则通常采用拉依达准则（又称3σ 准则）。

拉依达准则的判断式为

具体判断方法是：计算标准偏差，用±3σ 准则检查所有的残余误差vi。若某个vi的绝对值＞3σ，则该残余误差判断为粗大误差，予以剔除。然后重新计算剩余测量列的标准偏差，再用新算出的残余误差进行判断，直到剔除完为止。注意，每次操作只能剔除一个粗大误差。

拉依达准则主要用于服从正态分布的误差，重复次数又比较多的情况。还必须注意的是，当测量次数小于10次时，一般不能使用拉依达准则。

其他判断准则请参阅有关误差理论的书籍。

3.5.5.4　测量列中综合误差的处理

测量列的测得值中可能同时含有系统误差、随机误差和粗大误差，或者只含有其中某一类或某两类误差，因此应对各类误差分别进行处理，最后再综合分析，从而得出正确的测量结果。

（1）直接测量列的数据处理。

①判断测量列中是否存在系统误差，如存在，应设法加以消除和减小；②依次计算测量列的算术平均值、残余误差和任一测得值的标准偏差；③判断是否存在粗大误差，如存在，则应剔除并重新组成测量列；④重复上述计算，直到不含有粗大误差为止；⑤计算测量列算术平均值的标准偏差和测量极限误差；⑥确定测量结果，并说明置信概率。

下面通过例子说明直接测量列的数据处理的步骤和方法。

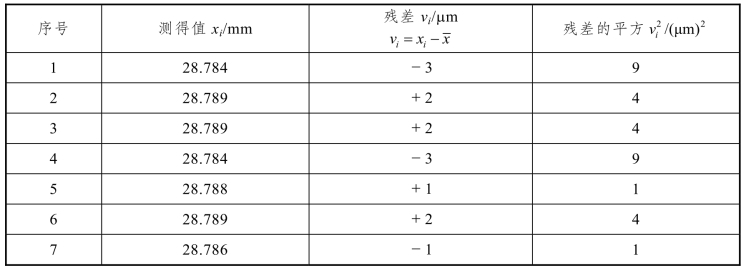
表3.3　数据处理计算表

(www.xing528.com)

续表

【例3-2】用立式光学计对某轴同一部位直径等精度测量12次，按测量顺序将各测得值列于表3.3，试求测量结果。

【解】①判断定值系统误差。假设计量器具已经检定、测量环境得到有效控制，可认为测量列中不存在定值系统误差。

②求测量列算术平均值。

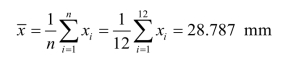
③计算残差vi=xi-，同时计算出，见表3.6。

④判断变值系统误差：根据残差观察法判断，测量列中的残差的符号大体上正、负相间，无明显规律变化，因此可以认为测量列中不存在变值系统误差。

⑤计算测量列单次测量值的标准偏差，得

⑥判断粗大误差。

由标准偏差，可求得粗大误差的界限，|vi|＞3σ＝5.7 μm。

按拉依达准则，测量列中没有出现绝对值大于5.7 μm的残差，即测量列中不存在粗大误差。

⑦计算测量列算术平均值的标准偏差，得

⑧计算测量列算术平均值的测量极限误差，得

⑨得出测量结果，即

这时的置信概率为99.73%。

（2）间接测量列的数据处理。

间接测量是指通过测量与被测几何量有一定关系的几何量，按照已知的函数关系式计算出被测几何量的量值。因此间接测量的被测几何量是测量所得到的各个实测几何量的函数。而间接测量的误差则是各个实测几何量误差的函数，故称这种误差为函数误差。

①函数误差的基本计算公式。

间接测量中，被测几何量通常是实测几何量的多元函数，它表示为

式中，y为被测几何量（函数）；xi为实测的几何量。

函数的全微分表达式为

式中，dy为被测几何量（函数）的测量误差；dxi为实测的几何量的测量误差；为各实测几何量的测量误差传递系数。

②函数系统误差的计算式。

由各实测几何量测得值的系统误差，可近似得到被测几何量（函数）的系统误差，其表达式为

式中，Δy为被测几何量（函数）的系统误差；Δx为实测几何量的系统误差。

式（3.22）表示各自变量直接测量的系统误差与函数系统误差的关系，即为函数系统误差的计算公式。

③函数随机误差的计算式。

由于各实测几何量的测得值中不可避免存在随机误差，因此，被测几何量（函数）也一定存在随机误差。根据误差理论，函数的标准偏差σy与各个实测几何量的标准偏差σxm有如下关系：

式中，σy为被测几何量（函数）的标准偏差；σxm为实测几何量的标准偏差。

式（3.23）表示了各独立自变量与其函数之间随机误差的关系，即为函数随机误差的计算公式。同理，如果各个实测几何量的随机函数符合正态分布，则被测几何量（函数）的测量极限误差的计算公式为

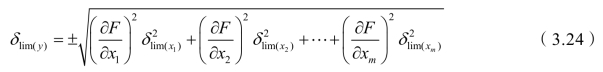
式中，δlim（y）为被测几何量（函数）的测量极限误差；为实测几何量的测量极限误差。

④间接测量列数据处理的步骤。

·确定函数表达式y＝F（x1，x2，…，x3）；

·求出被测几何量（函数）量值y；

·计算被测几何量（函数）的系统误差值Δy；

·计算被测几何量（函数）的标准偏差值σy和测量极限误差值；

·得出被测几何量（函数）的结果表达式并说明置信概率为99.73%。

【例3-3】用弦长弓高法测量圆弧样板半径R，已知测得值弓高h＝4 mm，弦长b＝40 mm，其系统误差分别为：Δh＝＋0.001 2 mm，Δb＝－0.002 mm。其测量极限误差分别为：δlim（h）＝±0.001 5 mm，δlim（b）＝±0.002 mm。试确定半径R的测量结果。

【解】①计算圆弧半径R：

②计算圆弧半径R的系统误差ΔR：

③计算圆弧半径R的测量极限误差δlim（R）：

④确定圆弧半径R的测量结果Re：

Re=(R-ΔR)±δlim(R)=[52-(-0.0194)]±0.0187=(52.0194±0.0187)mm

此时的置信概率为99.73%。