采用矩阵图形表示的最小度排序方案

方案0提供了简单而快速的排序方案，但没有直接考虑非零元注入对排序过程的影响。为了做到这一点，必须考虑排序过程中消去节点的影响。方案Ⅰ就是在此基础上的改进方案。

方案Ⅰ

1.计算所有节点的度。

2.选择度值最小的节点，对其进行编号；消去此节点并重新计算各节点的度。

3.如果出现度值相同的情况，原节点号小的节点优先排序。

4.返回步骤1。

方案Ⅰ具有多种名称，包括Markowitz算法^[31]，Tinney Ⅰ算法^[50]，或者最普遍地被称为最小度算法。

例4.8 利用方案Ⅰ对例4.6的矩阵重新排序并计算该排序下α、β的值以及非零元注入的数目。

解4.8 方案Ⅰ的排序考虑了当节点被消去后非零元注入对排序的影响。采用矩阵的图形表示可以最形象地表达这个算法。图4.10中未排序的原始矩阵所对应的图如图4.13所示。

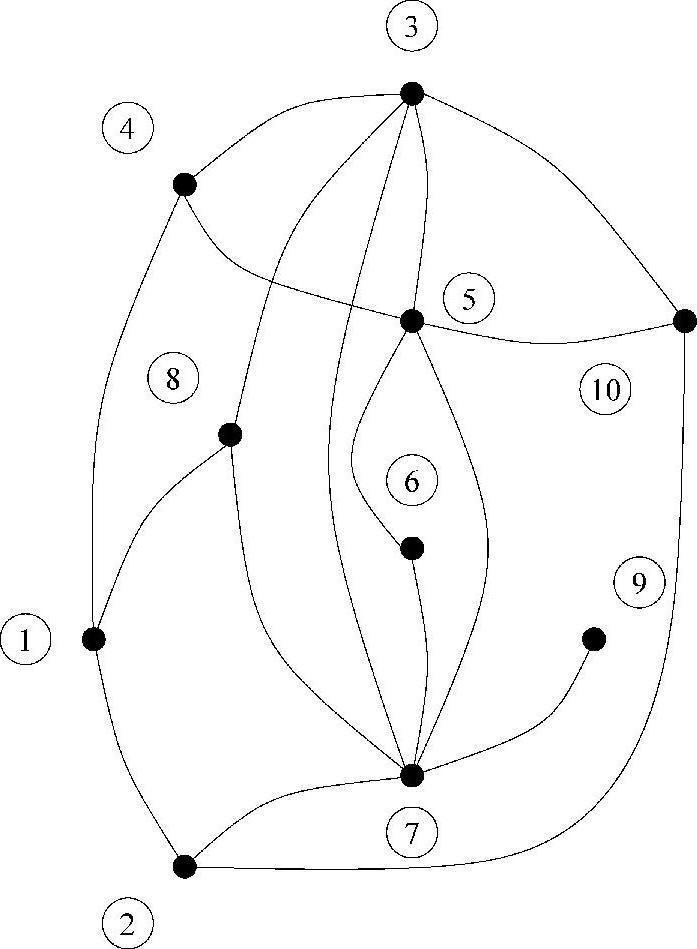
图4.13 图4.10中矩阵所对应的图

各个节点的度如下所示：

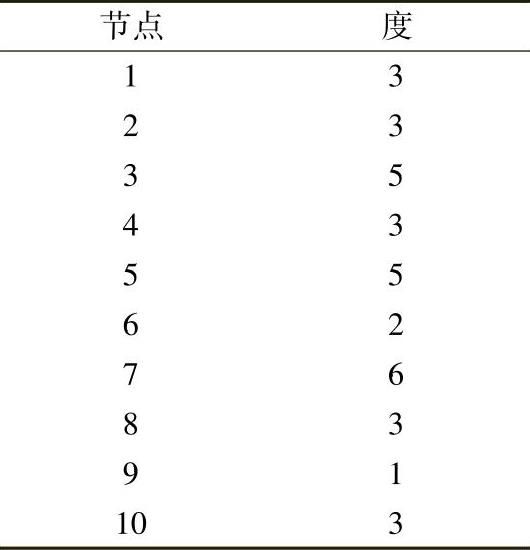
根据以上度的信息，具有最小度的节点优先排序。节点9只有一个连接，度值最小；消去节点9不产生任何非零元注入。更新后的图如图4.14所示。

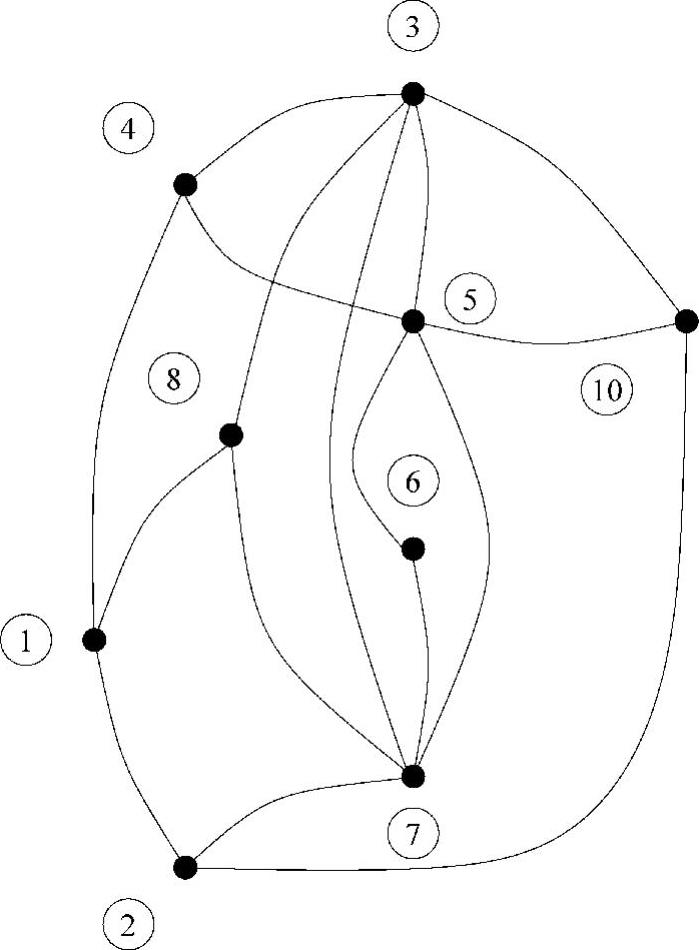
图4.14 消去节点9后更新的图

更新后各个节点的度如下所示：

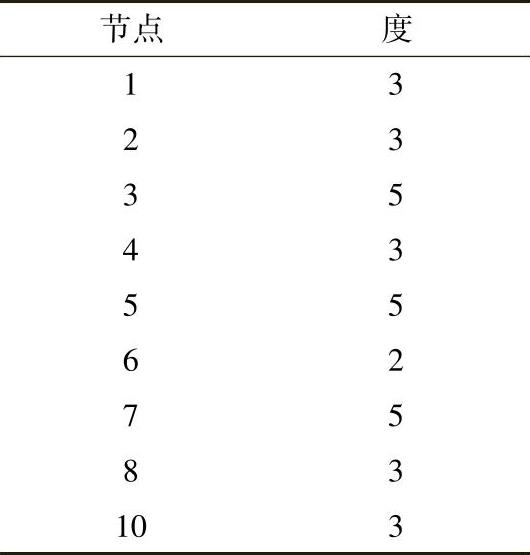
现在节点7的度少了1。再次采用方案Ⅰ的算法，发现下一个被选中的节点是度为2的节点6。节点6同时连接节点5和节点7。因为节点5与节点7之间已经有连接，消去节点6不会在节点5和节点6之间产生非零元注入。消去节点6后如图4.15所示。(www.xing528.com)

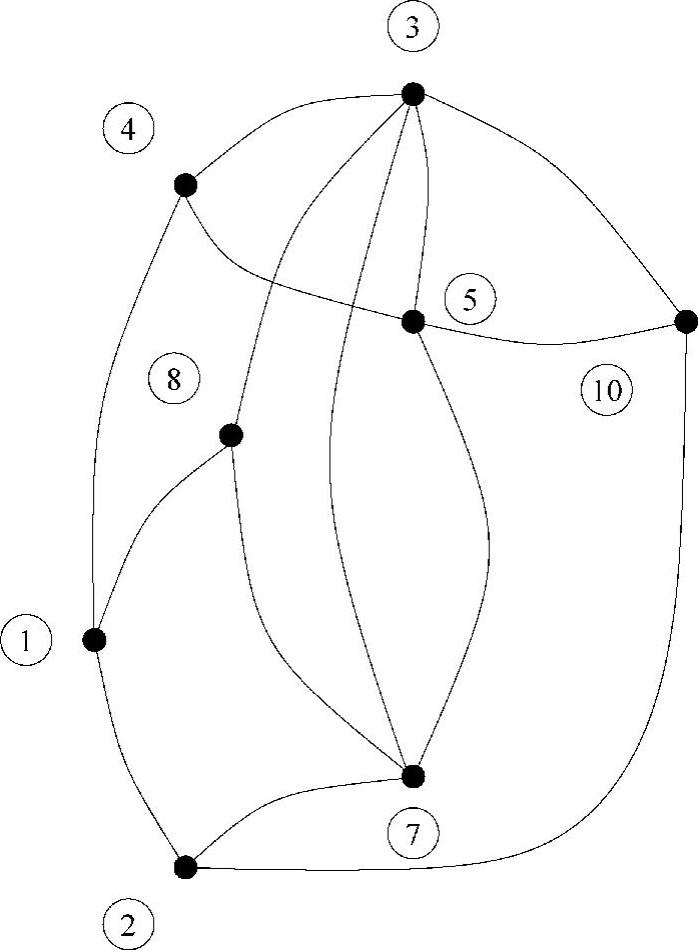
图4.15 消去节点6后的更新图

各节点的新的度如下所示：

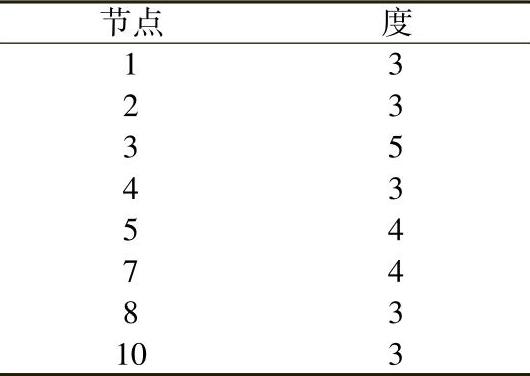
由于消去了节点6，节点5和节点7的度减小1。再次利用方案Ⅰ的算法，表明具有最小度的节点是[1 2 4 8 10]。因为这些节点的度相等，选择原节点号小的节点优先排序，即选择节点1消去。节点1与节点2、4、8相连接，而节点2、4、8之间不存在任何连接；因此消去节点1后产生3个非零元注入，即4-8、4-2和2-8。这些非零元注入如图4.16中的虚线所示。

消去节点1后各节点的新的度如下所示：

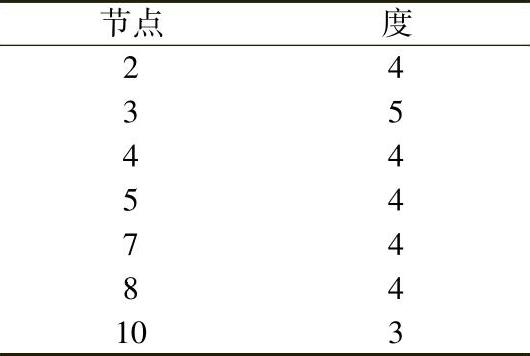
增加3个非零元注入后节点2、4、8的度上升了。再次利用方案Ⅰ的算法，表明具有最小度的节点是10，这次没有出现度值相等的情况。节点10被选中并消去。消去节点10在节点2-5和2-3之间产生了2个非零元注入，这些非零元注入如图4.17中的虚线所示。

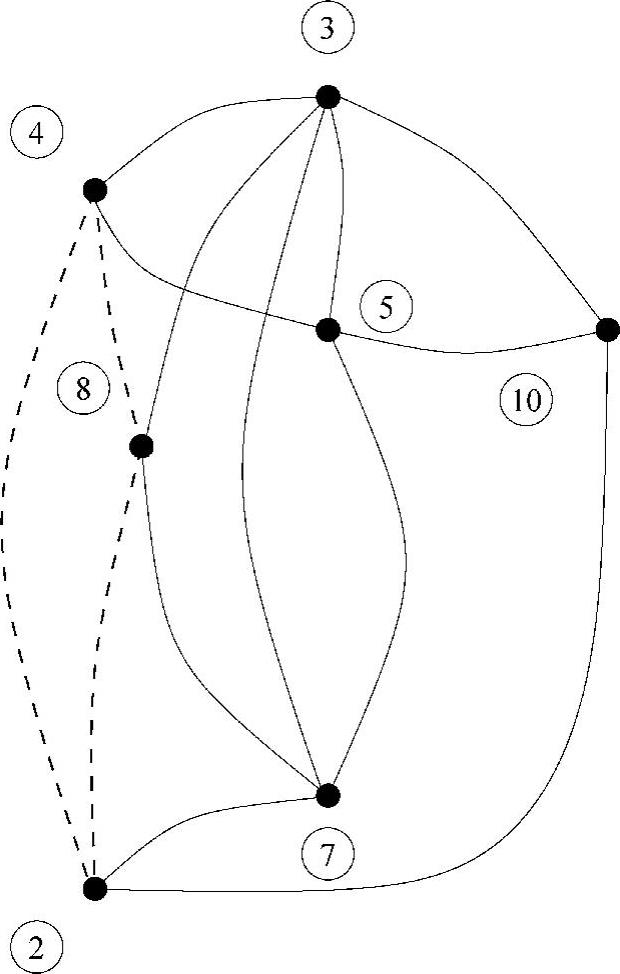
图4.16 消去节点1后更新的图

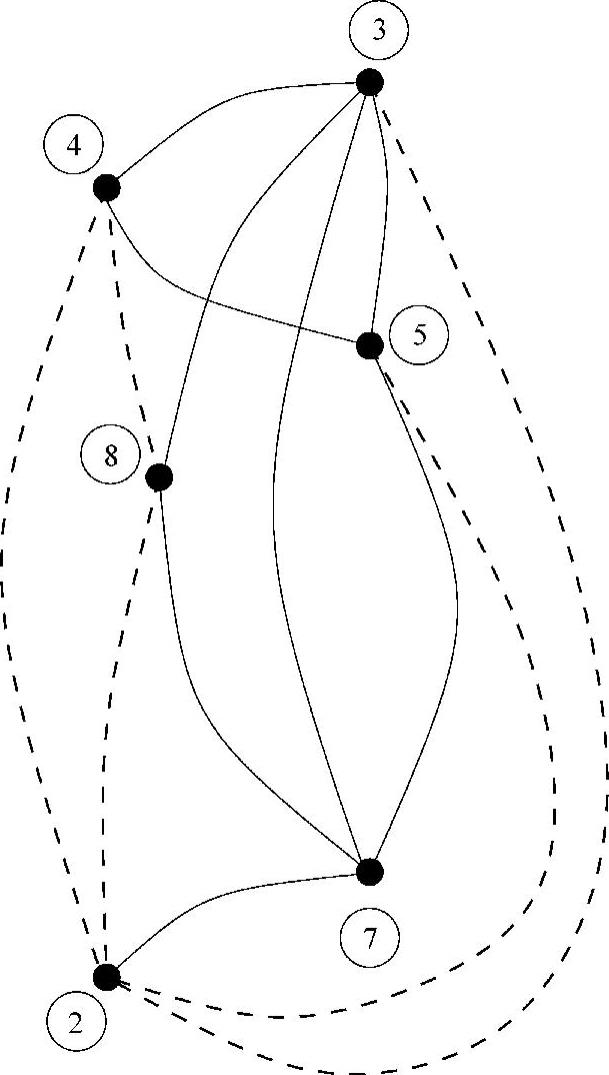
图4.17 消去节点10后更新的图

继续不断地使用方案Ⅰ算法直到所有节点都被选中并消去，可以得到最终的排序如下：

排序Ⅰ=[9 6 1 10 4 2 3 5 7 8]

根据上述排序重新排列例4.8中的矩阵，可以得到如图4.18所示（带非零元注入）的矩阵。注意，矩阵中的非零元排列构成了期望的指向右下方的箭头形状。方案Ⅰ排序产生了12个非零元注入，方案0排序产生了16个非零元注入，而原始排序产生的非零元注入是24个。针对此矩阵利用式（4.1）和式（4.2），可得到α=92和β=56，因此α+β=148，这相对于方案0的α+β=170和原始方案的α+β=202已有了相当大的减小。

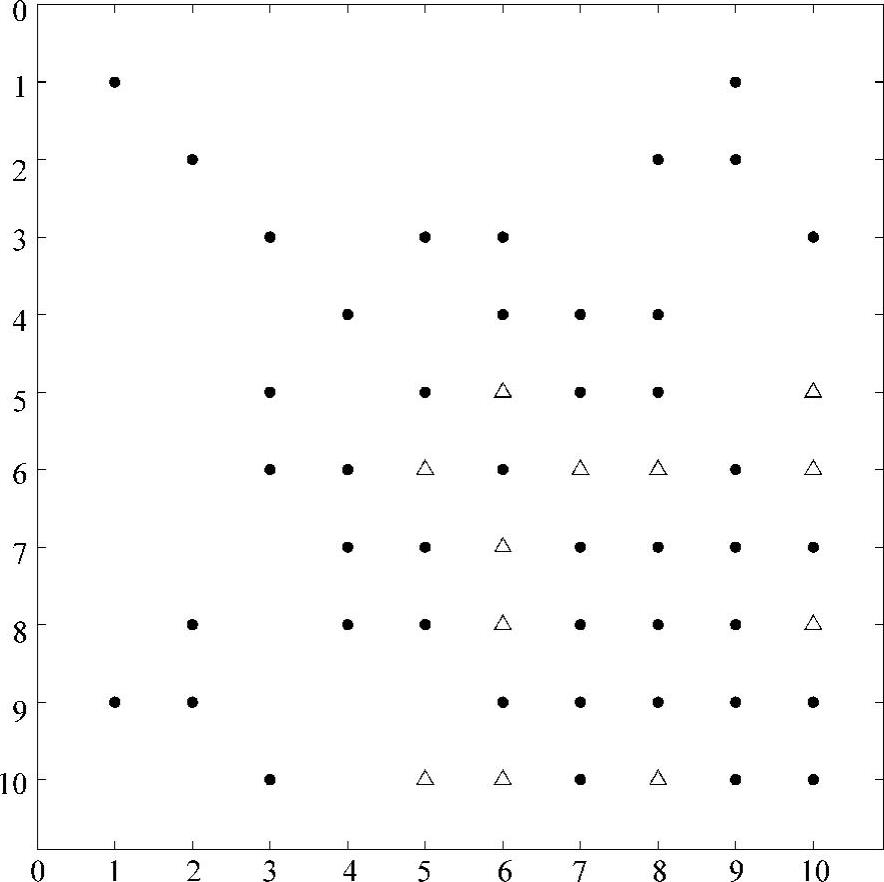
图4.18 加入非零元注入后例4.8的矩阵