齿轮接触点周围的共轭条件优化方案

运动参数为φ_j（j=1，2）时，齿面Σ₁以点M₁与齿面Σ₂的点M₂在固定空间点M接触。运动参数为φ_j+Δφ_j时，Σ₁与Σ₂以点M′₁和M₂′在点M′接触。当Δφ_j→0时，点M₁、M₂和M分别为点M′₁、M₂′和M′的极限位置，点M′₁、M₂′和M′则分别是点M₁、M₂和M满足共轭条件的邻域。根据上述定义，将式（1-8）～式（1-10）在静坐标系σ里微分，得到点M邻域的接触条件为

式（1-6）中微分V得到

将式（1-6）和式（1-17）代入式（1-16）得

由于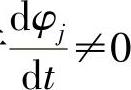，由式（1-18）得

dn₁·V_j+n₁·dV_j=0（j=1，2） （1-19）

为求得齿面Σ₁和Σ₂一些微分量之间的关系，将式（1-14）、式（1-15）和式（1-19）中关于静坐标系的普通微分变换成关于动坐标系σ₁和σ₂的相对微分^[10]。

式（1-14）中

将式（1-20）～式（1-22）代入式（1-14），并考虑到式（1-3）～式（1-7），得

式（1-23）还可以写成

同理可将式（1-15）中普通微分变成相对微分，有

式（1-16）中

由式（1-7）微分V_j得

将式（1-28）～式（1-32）代入式（1-27）得

将式（1-26）和式（1-33）代入式（1-18）得

式中，n_1u和n_1v分别为n₁对u和v的偏导数。

将式（1-36）和式（1-37）代入式（1-34）得(www.xing528.com)

n=2时，若将式（1-12）微分，可得到式（1-38）。由此可知式（1-38）中Φ_ju、Φ_jv、Φ_jφ1和Φ_jφ2是Φ_j对u、v、φ₁和φ₂的偏导数。

式（1-38）称为齿面接触点邻域共轭条件方程。

式（1-24）、式（1-25）和式（1-34）给出了齿面Σ₁和Σ₂接触点一些微分量之间的关系，可以避开齿面Σ₂繁复的方程，直接由齿面Σ₁及齿面Σ₁和Σ₂之间的相对运动参数，计算齿面Σ₂的法曲率和短程挠率等参数。

d₁r₁和d₂r₂在齿面接触点处的公切面上，它所确定的方向称为共轭方向。即由φ_j至φ_j+Δφ_j区间M₁M′₁沿着d₁r₁方向，则M₂M′₂沿着由式（1-24）确定的d₂r₂方向。通常两共轭方向不重合。

设过曲面上点M₁处，沿任一α方向曲线的弧长为s₁；沿关于φ_j的相对速度V_j方向曲线的弧长为s′₁。将式（1-41）代入式（1-34），除以ds₁后得

式中，。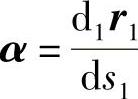

式（1-42）中

式中，下角“V_j”表示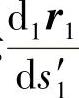为齿面Σ₁沿V_j方向的单位矢量；下角“α”表示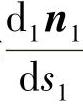为齿面Σ₁上n₁沿α方向的导矢。可以证明^[10]

于是

由微分几何可知

式中 κ_1Vj——齿面Σ₁沿V_j方向的法曲率；

τ_1Vj——齿面Σ₁沿V_j方向的短程挠率。

将式（1-44）代入式（1-43）得

将式（1-45）代入式（1-42）得