直接证明与间接证明的理解与应用

直接从原命题的条件逐步推得结论成立,这种证明方法叫直接证明.直接证明的两种基本方法——分析法和综合法,在证明方法中都占有重要地位,是解决数学问题的重要思想方法.当所证命题的结论与所给条件间联系不明确,常常采用分析法证明;当所证的命题与相应定义、定理、公理有直接联系时,常常采用综合法证明.在解决问题时,常常把分析法和综合法结合起来使用.

间接证明是不同于直接证明的又一类证明方法,反证法是一种常用的间接证明方法.反证法解题的实质是否定结论导出矛盾,从而说明原结论正确.在否定结论时,其反面要找对、找全.它适合证明“存在性问题、唯一性问题”,带有“至少有一个”或“至多有一个”等字样的数学问题.

方法简述

1.比较法

我们平时所说的比较法,只是单纯地作差(与0比)或作商(和1比),而作差更具有普遍性.作商时必须注意所比的两个数(或式)的符号.

事实上,要比较两个数的大小,许多时候仅用作差、作商的方法是绝对不能解决问题的,在作差或作商的基础上,还必须应用不等式证明时的一切方法.

(1)作差法:a≥b⇔a-b≥0;

(2)作商法

比较法是不等式证明的基本步骤和方法之一.它遵循“作差(或作商)—变形—判断”的解题规律.作差之后的配方或因式分解,有时确实是判断“差”的符号的关键.

例1 若实数x≠1,求证:3(1+x2+x4)>(1+x+x2)2.

点拨 在比较两个数或两个式子的大小时,可以使用作差或作商比较法.

∵x≠1,从而(x-1)2>0,且

∴

∴3(1+x2+x4)>(1+x+x2)2.

反思 通过作差比较法解题时,作差后一般要将式子整理成乘积或平方相关形式,便于判断它的正负.

例2 已知a、b∈R+,求证:aabb≥abba.

点拨 本题可以尝试使用作差比较和作商比较两种方法进行.

证明 作差比较法:要证的不等式关于a、b对称,不妨设a≥b>0.

∵a-b≥0,

∴aabb-abba=abbb(aa-b-ba-b)≥0,

从而原不等式得证.

作商比较法:设a≥b>0.

从而原不等式得证.

反思 比较法是证明不等式的一种最基本、最重要的方法.用比较法证明不等式的步骤是:作差(或作商)—变形—判断符号.

2.综合法

(1)定义

一般地,从命题的已知条件出发,利用公理、已知的定义及定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫作综合法.

(2)综合法的的基本思路

执因索果综合法又叫“顺推证法”或“由因导果法”.它是从已知条件和某些学过的定义、公理、公式、定理等出发,通过推导得出结论.

(3)综合法的思维框图

用P表示已知条件,Qi(i=1,2,3,…,n)为定义、定理、公理等,Q表示所要证明的结论,则综合法可用框图表示为:

例3 已知在x=x0处取最大值,以下各式正确的序号为(　).

①f(x0)<x0;②f(x0)=x0;③f(x0)>x0;④f(x0)<;⑤f(x0)>

A.①④　B.②④　C.②⑤　D.③⑤

点拨　此题是比较函数最大值,f(x0)与x0和的大小关系.用综合法推导f(x)的单调性及结论.

解答

由题意可知f'(x0)=0,

即lnx0+x0+1=0,lnx0=-(x0+1),

故

令函数g(x)=lnx+x+1(x>0),则

故函数g(x)为增函数,

而

∴,即.故选B.

反思 综合法的思维特点是由已知入手推出结论:

此题的推理是:①已知f(x0)最大⇒f'(x0)=0⇒f(x0)=x0;

②g'(x)>0⇒g(x)为增函数⇒

例4 已知a、b、c是不全相等的正数,求证

点拨 由基本不等式可得,代入原式很容易得到要证明的结论.

证明 ∵b2+c2≥2bc,

∴

同理可得

∵a、b、c是不全相等的正数,

∴b2+c2≥2bc,c2+a2≥2ac、a2+b2≥2ab三式中不能全取等号.

∴①②③三式也不能全取等号.

∴①②③三式相加,即a(b2+c2)+b(c2+a2)+c(a2+b2)>6abc.

反思 从本题的已知条件到要证明结论,显然利用综合法证明较方便,即使用均值不等式.但要注意使用均值不等式时,取“=”成立的条件.

3.分析法

(1)定义

一般地,从需要证明的命题出发,分析使这个命题成立的充分条件,逐步寻找使命题成立的充分条件,直至所寻求的充分条件显然成立(已知条件、定理、定义、公理等),或由已知证明成立,从而确定所证的命题成立的一种证明方法,叫作分析法.

(2)分析法的基本思路

执果索因分析法又叫“逆推证法”或“执果索因法”.它是从要证明的结论出发,分析使之成立的条件,即寻求使每一步成立的充分条件,直到最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止.

(3)分析法的思维框图

用Pi(i=1,2,3,…)表示已知条件和已有的定义、公理、公式、定理等,Q表示所要证明的结论,则用分析法证明可用框图表示为:

(4)分析法的格式

要证……,只需证……,只需证……,因为……成立,所以原不等式得证.

例5 已知函数f(x)=3x-2x,求证:对于任意的x1、x2∈R,均有

点拨　把分别用函数写出来,逐步分析要证的不等式.

证明 要证明

即证明

因此只要证明

即证明

因此只要证明

由于x1、x2∈R时,3x1>0,3x2>0,

由基本不等式知显然成立,

故原结论成立.

反思 分析法是数学中常用的一种直接证明方法,就证明程序来讲,它是一种从未知到已知(从结论到题设)的逻辑推理方法.具体地说,即先假设所要证明的结论是正确的,由此逐步推出保证此结论成立的充分条件,而当这些判断恰恰都是已证的命题(定义、公理、定理、法则、公式等)或要证命题的已知条件时命题得证.

4.反证法

(1)定义

一般地,首先假设要证明的命题结论不正确,即结论的反面成立,然后利用公理,已知的定义、定理,命题的条件逐步分析,得到和命题的条件或公理、定理、定义及明显成立的事实等矛盾的结论,以此说明假设的结论不成立,从而证明了原命题成立,这样的证明方法叫作反证法.

(2)反证法的特点

反证法是间接证明的一种基本方法.它是先假设要证的命题不成立,即结论的反面成立,在已知条件和“假设”这个新条件下,通过逻辑推理,得出与定义、公理、定理、已知条件、临时假设等相矛盾的结论,从而判定结论的反面不能成立,即证明了命题的结论一定是正确的.

(3)反证法的基本思路

“假设—矛盾—肯定”.

①分清命题的条件和结论;

②作出与命题结论相矛盾的假设;

③由假设出发,结合已知条件,应用演绎推理方法,推出矛盾的结果;

④断定产生矛盾结果的原因,在于开始所作的假设不真,于是原结论成立,从而间接地证明原命题为真.

(4)用反证法证明命题“若p则q”,它的全部过程和逻辑根据可以表示为:

(5)反证法的优点

对原结论否定的假设的提出,相当于增加了一个已知条件.(www.xing528.com)

(6)用反证法证明数学命题的一般步骤

①反设——假设命题的结论不成立,即假定原命题的反面为真;

②归谬——从反设和已知条件出发,经过一系列正确的逻辑推理,得出矛盾结果;

③存真——由矛盾结果,断定反设不真,从而肯定原结论成立.

(7)适合使用反证法的数学问题

①要证的结论与条件之间的联系不明显,直接由条件推出结论的线索不够清晰,比如“存在性问题、唯一性问题”等;

②如果从正面证明,需要分成多种情形进行分类讨论,而从反面进行证明,只要研究一种或很少的几种情形,比如带有“至少有一个”或“至多有一个”等字样的数学问题.

例6 已知函数,请用反证法证明f(x)=0没有负实数根.

点拨 假设有负数根,根据指数函数性质证出矛盾.

证明 证法一:设存在x0<0(x0≠-1),满足f(x0)=0,则

因为,所以,与假设x0<0矛盾.

故方程f(x)=0没有负实数根.

证法二:设存在x0<0(x0≠-1),满足f(x0)=0.

①若-1<x0<0,则,所以f(x0)<-1与f(x0)=0矛盾.

②若x0<-1,则,所以f(x0)>0与f(x0)=0矛盾.

故方程f(x)=0没有负数根.

反思 反证法的关键是在正确的推理下得出矛盾,矛盾可以是:①与已知条件矛盾;②与假设矛盾;③与定义、公理、定理矛盾;④与事实矛盾等方面,反证法常常是解决某些“疑难”问题的有力工具,是数学证明中的一件有力武器.

例7 若a、b、c均为实数,且

求证:a、b、c中至少有一个大于0.

点拨 至少有一个大于0的情况很多,直接证明有困难,而它的反面是都不大于0比较好证明,所以考虑用反证法来证明.

证明 假设a、b、c都不大于0,即a≤0,b≤0,c≤0,则有a+b+c≤0.

∵(x-1)2,(y-1)2,(z-1)2均大于或等于0,π-3>0,

∴a+b+c>0,这与假设a+b+c≤0矛盾,故a、b、c中至少有一个大于0.

反思 先假设a、b、c都不大于0,然后通过已知推导出a+b+c>0与假设矛盾,所以原题结论正确.当一个命题的结论是以“至多”“至少”“唯一”或以否定形式出现时,宜用反证法来证明.

5.放缩法

所谓放缩法,即要把所证不等式的一边适当地放大或缩小,以利于化简,并使它与不等式的另一边的不等关系更为明显,从而得到欲证的不等式成立.

例8 已知an=2n-1(n∈N*),求证

点拨 在整理过程中,观察所证明的结论,采用放缩法,舍去2k-2,从而使和式得到化简.

反思 若多项式中加上一些正的值,多项式的值变大,多项式中加上一些负的值,多项式的值变小.由于证明不等式的需要,有时需要舍去或添加一些项,使不等式一边放大或缩小,利用不等式的传递性,达到证明的目的.

例9 已知函数,求证

点拨 此题不等式左边不易求和,此时根据不等式右边特征,先将分子变为常数,再对分母进行放缩,从而对左边可以进行求和.

反思 若分子、分母同时存在变量时,要设法使其中之一变为常量,分式的放缩对于分子、分母均取正值的分式,如需放大,则只要把分子放大或分母缩小即可;如需缩小,则只要把分子缩小或分母放大即可.

6.数学归纳法

设{Pn}是一个与自然数相关的命题集合,如果:①证明起始命题P1(或P0)成立;②在假设Pk成立的前提下,推出Pk+1也成立,那么可以断定{Pn}对一切自然数成立.

例10 用数学归纳法证明2n+2>n2(n∈N*).

点拨 使用数学归纳法时,要根据证明的需要来选取起始命题,而本题只证n=1显然不够.

证明 ①当n=1时,21+2>12,不等式成立;

当n=2时,22+2>22,不等式成立;

当n=3时,23+2>32,不等式成立.

②假设当n=k(k≥3,k∈N*)时,不等式成立,即2k+2>k2.

则当n=k+1时,2k+1+2=2(2k+2)-2>2k2-2=(k+1)2+k2-2k-3,

∵k≥3,∴k2-2k-3=(k-3)(k+1)≥0,

从而2k+1+2>(k+1)2+k2-2k-3≥(k+1)2,

∴2k+1+2>(k+1)2.

即当n=k+1时,不等式也成立.

由①②可知,2n+2>n2对一切n∈N*都成立.

反思 因为在k2-2k-3=(k-3)(k+1)≥0处,当k≥3时才成立,故起点只证n=1还不够,因此我们需注意命题的递推关系式中起点位置的推移.

易错解读

易错点1 归纳过程中考查个体不够.

在使用不完全归纳法时,由于缺乏验证过程,所以结论可能有误,所以在归纳时要尽量多选取一些特值,力求使结果更准确.

例11 已知数列{an}满足,试归纳出这个数列的通项公式.

解答 错解:

经过计算可知

除第一个外,后三个很有规律,

于是猜想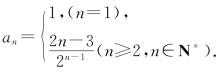

正解:

猜想

反思 本题错解中容易验证,当n=5时,就不适合,原因是由归纳推理所得的结论未必是可靠的.一般地,考查的个体越多,归纳的可靠性越大.

易错点2 反证法第一步假设过程中特殊词否定不准确.

在反证法中,第一步假设时注意一些特殊词的否定形式,避免发生错误.

例12 用反证法证明命题“设a、b为实数,则方程x2+ax+b=0至少有一个实根”时,要作的假设是(　).

A.方程x2+ax+b=0没有实根

B.方程x2+ax+b=0至多有一个实根

C.方程x2+ax+b=0至多有两个实根

D.方程x2+ax+b=0恰好有两个实根

解答 反证法的步骤中的第一步是假设命题反面成立,而“方程x2+ax+b=0至少有一实根”的反面是“方程x2+ax+b=0没有实根”,故选A.

反思 注意常见词语的否定.

原词语:大于(>);小于(<);都是;至多有一个;至少有一个;至多有n个.

否定词语:不大于(≤);不小于(≥);不都是;至少有两个;一个也没有;至少有n+1个.

经典训练

1.下列证明方法中属间接证法的是(　).

A.综合法　　　B.分析法　　C.反证法　　D.数学归纳法

2.用反证法证明:“a>b”.应假设(　).

A.a>b　B.a<b　C.a=b　D.a≤b

3.设x、y为正数,则的最小值为(　).

A.6　B.9　C.12　D.15

4.实数a、b、c不全为0的条件是(　).

A.a、b、c均不为0　B.a、b、c中至少有一个为0

C.a、b、c至多有一个为0　D.a、b、c至少有一个不为0

5.数列{an}满足an+1=an-an-1(n≥2),a1=a,a2=b,设Sn=a1+a2+…+an,则下列结论中正确的是(　).

A.a100=-a,S100=2b-a　B.a100=-b,S100=2b-a

C.a100=-b,S100=b-a　D.a100=-a,S100=b-a

6.用反证法证明:“f(n)被4除余1”,应假设________即________.

7.设实数a、b、c成等比数列,非零实数x、y分别为a与b,b与c的等差中项,则=______.

8.证明:若x、y>0,且x+y>2,则中至少有一个小于2.

9.设x>0,y>0,求证

10.在△ABC中,已知,且cosA=cosC,求证:△ABC为等边三角形.

11.关于复数z的方程z2-(a+i)z-(i+2)=0(a∈R),求证:对任意的实数a,原方程不可能有纯虚根.