水文学概论：河道汇流过程的水量平衡方程

河道汇流过程是洪水波运动过程。

1.河道洪水波

无雨条件下，河道中的水流呈稳定流状态，其水面线如图7.17中虚线所示。当流域上发生暴雨时，大量地表径流汇入河道，使得河道中流量急剧增大，形成洪水波。河道中的洪水波呈不稳定流状态，洪水波要素也如图7.17所示。s为波峰，h为波高，ac为波长，sc部分为波前，as部分为波后，而洪水波的水面线为asc。洪水波的波长比波高大数千乃至数万倍，属某种“超长波”。在稳定流水面线以上部分称为波流量，随着洪水波向下游的波体运动而带走水量。洪水波不同于风波、振动波，洪水波运动随时间变化相当缓慢，属于缓变不稳定流。

图7.17　洪水波要素示意图

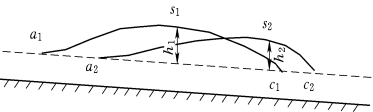
图7.18　洪水波运动变形示意图

洪水波水面比降与相应水位下稳定流的水面比降i0的差值称为附加比降iΔ，天然河道洪水波的附加比降较小，常不到0.0001；然而其稳定流水面比降也很小，约0.001左右；因而iΔ/i0的值就会在百分之几乃至十分之几，这就不可忽略了。

因为附加比降，引起波前及波后的比降和水深不同，又因河道特性的影响，洪水波发生变形。在棱柱型河道内，洪水波自t1时刻的a1s1c1传播到t2时刻的a2s2c2时，洪水波波前sc部分的比降大于波后as部分，因而波前运动速度大于波后，使得运动过程中波长不断增加，波高则不断降低，即a1c1＜a2c2且h1＞h2，如图7.18所示。这类现象通常称作洪水波的展开。

由于洪水波各处的水深不同，波峰处最大，运动速度也最快，因此运动中波前长度逐渐减小，比降逐步增大，波峰位置不断提前；而波后长度逐渐拉长，比降逐步变缓；这类现象则称为洪水波的扭曲。

依据洪水波的形成与运动特点，洪水波运动可采用圣维南（Saint-Venant）方程组描述，在无支流汇入的河段，其连续方程和能量方程分别如下所示

式中　Q——断面流量，m3/s；

A——过水断面面积，m2；

l——河长，m；

t——时间，s；

v——断面平均流速，m/s；

g——重力加速度，m/s2；

y——水深，m；

sf——摩阻比降，‰；

s0——河底比降，‰。

式（7.28）也可以称为动力方程，它反映了洪水波运动过程中各种作用力的动平衡，各项意义依次为：①局地惯性项；②空间惯性项；③附加比降，代表了压力项；④摩阻比降，代表了阻力项；⑤河底比降，代表了重力项。考虑河段具体情况，可作出不同简化方法。仅考虑④、⑤两项，称为运动波；考虑③、④、⑤3项，称为扩散波；考虑①、②、③3项，称为惯性波；5项全考虑称为动力波。下面仅仅阐述运动波、扩散波的特性。

（1）运动波。山区河流河底比降s0较大，洪水波近似于运动波。它假定惯性项和附加比降项与河底比降相比小很多，因而可忽略不计。依据谢才（Chezy）公式，摩阻比降sf为

将上式代入式（7.28），并忽略惯性项和附加比降项，则有

式中　K——流量模数，。

由于流量模数K是断面形状和水深的函数，式（7.30）表明对于特定断面，水位与流量呈单值关系，结合连续方程（7.27）可推导得

其中　

式（7.31）、式（7.32）表明运动波总是向下游传播且波速为Ck，在运动波传播过程中，任一相应流量都不发生变化。这意味着运动波没有坦化现象，是否变形取决于波速Ck为常数与否。由于波速是随水深和流量而变化的函数，通常水深是沿流程变化的，因而运动波一般存在着扭曲变形，即波前越来越陡，如图7.19所示。

图7.19　运动波的传播与变形

运动波条件下，其特定断面水位-流量关系多数情况下呈单值关系。

（2）扩散波。对于河底比降s0较小的河段，附加比降∂y/∂l的作用不能忽略，二者之和比惯性项仍大时，可用扩散波描述，其能量方程可简化为

式中　Q0——稳定流时的流量，m3/s；

其余符号同前。

由于∂y/∂l随洪水涨落变化，涨洪时∂y/∂l＜0，落洪时∂y/∂l＞0，从而涨洪时，故Q＞Q0；落洪时，而Q＜Q0。这表明在此条件下水位-流量关系不是单值函数，同一水位时将有两个流量与之对应。亦即一次洪水过程中，若按时间顺序连接，水位-流量关系是一条逆时针方向的绳套形曲线，如图7.20所示。而绳套的大小取决于∂y/∂l与s0的比值，一般而言，（1/s0）（∂y/∂l）越大，绳套也越大。

图7.20　扩散波的水位-流量关系

结合连续方程（7.27）可推导得

其中　

式（7.34）、式（7.35）表示扩散波以波速Ck向下游传播，沿前进方向相应流量会产生变化，而变化程度取决于μ和∂2Q/∂l2两个因素，其中，μ为扩散系数，又称作衰减系数。当μ=0时，式（7.34）即为运动波方程，也就是说运动波属于扩散波的一个特例。

2.槽蓄原理与特征河长

（1）河段水量平衡方程。将描述洪水波运动的连续方程式（7.27）写为有限差分形式，即

以ΔQ=Q-I，ΔW=ΔAΔl；此处ΔW为时段Δt内河槽蓄水量，代入上式有

式中　——时段Δt内的平均入流量和出流量。

若流量在Δt时段内为直线变化，式（7.37）应为

其中，脚标1，2分别表示Δt时段的始、末取值。(www.xing528.com)

式（7.38）即为有限时段Δt内河段的水量平衡方程，如图7.21所示。

（2）槽蓄方程。河段的槽蓄水量取决于河段中水位的沿程分布状况，也就是水面曲线的形状。由于河段任意断面水位与流量存在着某种关系，故河段槽蓄水量是流量沿程分布和断面水位-流量关系的函数，称此函数为槽蓄方程。

图7.21　河段水量平衡示意图

图7.22　稳定流条件下的槽蓄方程

在稳定流条件下，槽蓄方程表达的是槽蓄水量与稳定流量之间的函数关系，可写为W=f（Q0），其中，W为河段槽蓄量，Q0为河段中的稳定流量；如图7.22所示。

在洪水波条件下，槽蓄方程十分复杂。为了便于理解，假设河段的水位沿程分布呈直线，如图7.23（a）所示。当河段的中断面水位不变时，河段中槽蓄量也不变。这意味着，当河段水面线呈直线时，其中断面水位与河槽蓄量为单一关系，如图7.23（b）所示。但是，由于附加比降的影响，中断面水位与下断面流量存在3种关系。在中断面水位不变条件下：①下断面涨洪时的流量小于落洪时的流量，中断面水位与下断面流量呈逆时针绳套曲线关系；②下断面涨、落洪时的流量相等，中断面水位与下断面流量呈单值关系；③下断面涨洪流量大于落洪流量，中断面水位与下断面流量呈顺时针绳套曲线关系；分别如图7.24的（a）、（b）、（c）所示。这表明在特定河段，槽蓄量W与下断面流量Q的关系有可能成为单值关系。

图7.23　洪水波水面线与中断面水位-槽蓄量关系

（3）特征河长。加里宁（Kалинин）和米留柯夫（Милюкав）提出了特征河长的概念，它指在特定河长条件下，其下断面处由于水位变化引起的流量变化，与水面比降引起的流量变化抵消，从而使河段槽蓄量W与下断面流量为单值关系。提出这一概念是基于下述分析：中断面水位不变时，涨洪阶段上断面先涨，下断面后涨，下断面水位比稳定流时降低，使下断面流量减小；而此时水面比降由于有附加比降，又会使流量加大。落洪时，鉴于上断面先落，下断面后落，状况与涨洪时刚好相反。因而存在着这样一种特征河长，如图7.25所示。

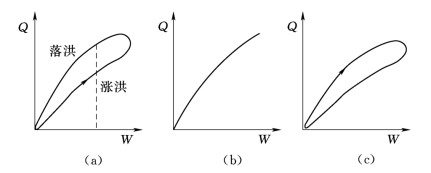
图7.24　洪水波条件下的槽蓄曲线3种形式

图7.25　特征河长示意图

由水力学可知，任意断面的流量是水位z和水面比降s的函数，即Q=f（z，s）。取全微分，有

就特征河长而言，当中断面水位z不变时，下断面流量不变，即dQ=0，并且d z=-（1/2）l ds，代入上式，故有

所以　

在稳定流情势下，可应用曼宁公式计算流量，，对其微分有

将式（7.42）代入式（7.41）得

若各项均取稳定流数值，那么可得到特征河长近似计算公式

式中　——稳定流时水位-流量关系的斜率。

式（7.44）表明，在特征河长条件下，槽蓄方程为W=Kl Q，其中，Kl为特征河长的传播时间，取为常数。

综上所述，特征河长是河道水力特性的综合参数。而河道水力特性也决定了洪水波运动的特点，所以特征河长与河道洪水波有着密切关系。

图7.26　马斯京根槽蓄量示意图

特征河长是个重要概念，在河道汇流计算中常用特征河长作为单元河段推求汇流曲线及其参数，在水文资料整编中，也利用特征河长实现水位流量关系的单值化。

例如，马斯京根河道洪水演算方法就是基于特征河长原理，假定河段槽蓄由两部分构成，一是柱蓄，即位于某平行于河底的线以下的蓄量；二是楔蓄，即此线与水面线间的蓄量；如图7.26所示。将上断面入流水量引入河段水量平衡方程，则槽蓄量可表示为入流量与出流量的函数，且槽蓄量等于柱蓄量与楔蓄量之和，于是有

式中　a、n——河段平均水位-流量关系Q=azn中的系数和指数；

b、m——河段平均水位-蓄量关系W=bzm中的系数及指数，对于宽浅矩形断面，m≈1.0；对于有漫滩的天然河道，n接近于1或小于1；

x——权重系数，表示在特定槽蓄量时，入流量与出流量的相对比重，反映楔蓄对流量演算的作用，x大楔蓄作用大，x小则楔蓄作用小，若入流等于出流则x=0.5。一般天然河道的x值在0.1～0.4之间。设m/n=1.0，且b/a=k，则有

再设Q′=x I+（1-x）Q，则

式（7.46）或式（7.47）就是马斯京根法的槽蓄曲线方程，式中Q′为示储流量。

依据上述分析，可知特征河长为l时，实际河长L＞l，L=l，L＜l分别对应于河段槽蓄量与下断面流量逆时针绳套关系、单值关系和顺时针绳套关系。

（4）河段洪水传播时间τ。洪水波在微小河段d x距离内的传播时间dτ为，且洪水波波速Ck=dQ/d A，可得

于是，洪水波在河段L内的传播时间为

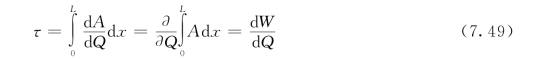
式（7.49）表明河段传播时间是槽蓄量对流量的导数，若以差分方式表达则为

即当河段蓄量W为流量Q的单值函数时，槽蓄曲线的斜率就是传播时间。这也说明了马斯京根方程的k等于稳定流条件下的传播时间。

3.线性洪水演算

水文情报预报和水文水资源分析计算的重要任务之一是依据上断面洪水过程推算下断面洪水过程，通常称为洪水演算或流量演算，其实质是河段洪水汇流。这里仅简单介绍线性扩散波洪水演算的原理，其应用细节将在“水文情报预报”和“水文水资源分析计算”课程中讲述。

所谓线性扩散波是指描述扩散波的方程中的μ和Ck为常数，此时它属于线性微分方程。而线性扩散波洪水演算首先是采用简单入流函数的组合来逼近实际的入流洪水过程线；然后利用线性微分方程的特性将用简单入流函数组合的上断面的入流洪水过程演算成下断面的出流洪水过程。在具体演算时通常是采用河段汇流曲线法。所谓河段的汇流曲线是指当河段上断面的入流为简单入流时在河段下断面所形成的出流过程线。

常用的简单入流有单位入流、单位矩形入流以及单位瞬时脉冲入流。单位入流是指始终保持一个单位强度的入流；单位矩形入流是指在一定时段内保持一个单位强度的入流；单位瞬时脉冲入流是指强度无穷大，历时无穷小而总量为一个单位时的入流。按河段汇流曲线的定义，河段汇流曲线有3种：①河段上断面的单位入流在下断面所形成的出流过程线称为S（t）曲线；②河段上断面的单位矩形入流在下断面所形成的出流过程线称为时段单位线u（Δt，t）；③河段上断面的单位瞬时脉冲入流在下断面所形成的出流过程线称为瞬时单位线u（t）。依据各种简单入流之间的关系，S（t）曲线是瞬时单位线的积分曲线，即；而u（Δt，t）=S（t）-S（t-Δt）。至于如何采用这些河段汇流曲线进行洪水演算将在水文情报预报课程中介绍。