薄透镜的位相调制效果

所谓薄透镜，是指透镜的最大厚度（透镜两表面在其主轴上的间距）与透镜表面的曲率半径R1、R2相比可以忽略的透镜。在薄透镜近似下，若一条光线从透镜前表面上坐标为（x，y）的点射入，则在其后表面上也将从近似相同的坐标处射出，即忽略光线在透镜内的偏移，而只考虑入射光波受到的位相延迟。

在图3.1.1中，由点源O发出的发散球面波，经过透镜L后，会聚到I点处，成为点源O的像。设在透镜的两顶点处分别作两个垂直于主光轴的参考平面P1、P2与之相切，则由薄透镜定义知，光线在P1平面上的入射点与在P2平面上的出射点高度相等，可以用同一坐标（x，y）表示，且认为这两个平面上对应的光扰动的振幅值也是相等的。再根据菲涅耳近似知，由O点发出的球面波到达P1平面上某点（x，y）处时，其复振幅可表示为

图3.1.1　透镜对入射光波面的作用

式中，因子对现在的讨论无关紧要，可以略去，故写成

上式称为球面波的二次曲面近似，等于常数的平面称为广义等位相面（Generalized Isophase Surface）。

由于点物O成像在I点，则根据光路可逆性原理，该球面波在透镜后P2平面上的光场也可看成是由I点向左发出的半径为d2的球面波，其在P2平面上的二次曲面近似可表示为

于是，透镜的透过率函数PL（x，y）可定义为

按照透镜成像的公式，有

f是透镜的焦距，由下式计算：

式中，n为透镜材料折射率。(www.xing528.com)

式（3.1.3）中再略去与x、y无关的常数因子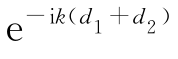后，可以写成

由于PL（x，y）的幅值为1，所以透镜是一个位相物体，它仅改变入射光波的位相分布。对于一个沿透镜主光轴入射的平面波而言，通过透镜后的出射光波，其位相分布就是PL（x，y），可以把它看成是半径为f的球形波面的二次曲面近似。

式（3.1.4）是在假定透镜孔径为无限大的前提下推导出来的。如果考虑到透镜孔径的有限大小对光场分布的影响，则对式（3.1.4）还必须乘以透镜的孔径函数P（x，y）或称光瞳函数（Pupil Function），其定义为

式中，r0是透镜圆形孔径的半径。于是，透镜的透过率函数的更一般的表示式应写为

式中，P′L（x，y）又称为透镜作用因子，φ（x，y）=（x2+y2）称为位相变化函数。虽然这个位相变化函数在图3.1.1中是根据双凸透镜推导出来的，但只要按照几何光学中关于焦距正负号的规则，式（3.1.4）就同样适用于各种形式的透镜，例如，对于双凸透镜、平凸透镜、正弯月形透镜而言，其焦距f＞0，称为正透镜；对于双凹透镜、平凹透镜、负弯月形透镜而言，其焦距f＜0，称为负透镜（见图3.1.2）。另外，应当注意到，透镜对入射光的位相变换作用，是由透镜本身的性质决定的，而与入射光的复振幅无关。为了理解式（3.1.4）的物理意义，现以单位振幅的平面波垂直入射到透镜上，并就会聚透镜和发散透镜两种情况，分析透镜的位相调制作用。在此情况下，由于入射波的振幅为1，则透镜后表面的复振幅应为

图3.1.2　各种类型的透镜

在近轴条件下，这是一个球面波的表达式。说明由于透镜的位相变换作用，使平面波变成了球面波。对于正透镜（f＞0），这是一个向透镜后方距离f处的焦点F′会聚的球面波〔见图3.1.3（a）〕；对于负透镜（f＜0），这是一个由透镜前方距离-f处的虚焦点F′发出的发散的球面波〔见图3.1.3（b）〕。因此，焦距为正的透镜是会聚透镜，而焦距为负的透镜是发散透镜。

图3.1.3　正透镜和负透镜对垂直入射平面波的效应

最后指出，如果某种器件或者透明图片对光波的复振幅透过率可用式（3.1.4）来表示，则其作用就相当于焦距为f的透镜。