大学应用数学：函数极限

若在自变量的某个变化过程中，函数f（x）无限接近于一个确定的常数A，则称A为函数f（x）在该变化过程中的极限.下面就自变量的不同变化趋势，分别介绍函数的极限.

1.x→∞时函数f（x）的极限

定义1.7　设函数y=f（x）在（-∞，+∞）内有定义，若当|x|无限增大时，相应的函数值f（x）无限接近于某一确定的常数A，则A称为函数f（x）当x→∞时的极限，记作

其中，“x→∞”表示x既可取正值且无限增大，也可取负值且绝对值无限增大.但有时x只能或只需取这两种变化中的一种情形同理可得x→+∞或x→-∞时函数f（x）的极限定义.

定义1.8　设函数y=f（x）在[a，+∞）（a为某个实数）内有定义，如果当自变量x取正值且无限增大时，相应的函数值f（x）无限接近于某一确定的常数A，则称A为函数f（x）当x→+∞（读作“x趋于正无穷大”）时的极限，记作

定义1.9　设函数y=f（x）在（-∞，a]（a为某个实数）内有定义.如果当自变量x取负值且无限减小（或-x无限增大）时，相应的函数值f（x）无限接近于某一确定的常数A，则称A为函数f（x）当x→-∞（读做“x趋于负无穷大”）时的极限，记作

上述定义从直观上描述了函数当自变量x→∞，x→+∞和x→-∞时的变化趋势，通常借助函数的图像去理解是比较容易的.

不难证明，函数f（x）当x→∞时的极限与当x→+∞，x→-∞时的极限有如下关系.

定理1.2　极限的充分必要条件是

例1.7　分析的存在性.

解　由图1.8知，

图1.8

由定理1.2知，不存在.

2.x→x0时函数f（x）的极限

首先介绍邻域的概念.

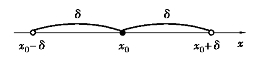
图1.9

设x0，δ∈R，实数集合{x||x-x0|＜δ，δ＞0}称为点x0的δ邻域，记作U（x0，δ）.由于不等式|x-x0|＜δ⇔x0-δ＜x＜x0+δ⇔x∈（x0-δ，x0+δ），所以邻域U（x0，δ）实质上表示以点x0为中心，长度为2δ的开区间（见图1.9），即(www.xing528.com)

U（x0，δ）={x||x-x0|＜δ，δ＞0}=（x0-δ，x0+δ）.

其中x0称为邻域中心，δ称为邻域半径.有时还要用到去掉中心的邻域，叫作去心邻域.点x0的去心δ邻域记作，即

定义1.10　设函数f（x）在点x0的某去心邻域U。（x0，δ）内有定义.若当自变量x在该邻域内无限接近于x0时，函数f（x）无限接近于某一确定的常数A，则称A为函数f（x）当x→x0时的极限，记作

例1.8　设函数.当x≠2时，f（x）=x+2.当自变量x≠2且无限接近于2时，对应的函数值无限接近于常数4（见图1.10）.

图1.10

必须注意的是：（1）当x→x0时，函数f（x）的极限是否存在，与函数在x=x0处是否有定义无关.

（2）在函数极限的定义中，x→x0的方式是任意的，即同时从x0的左右两侧无限接近x0.

但有时只需或只能考虑自变量x从x0的某一侧无限接近于x0的情况，就有下列单侧极限的定义.

定义1.11　设函数f（x）在点x0的某左半邻域（x-δ，x0）内有定义，当x从x0的左侧趋于x0时（记作），函数f（x）无限接近于某一确定常数A，则称A为函数f（x）在点x0处的左极限，记作

类似地，可以给出函数f（x）在点x0处的右极限定义，右极限记作

函数的右极限和左极限统称为单侧极限.相应地将称为双侧极限，简称极限.

由上述定义可知，单侧极限与双侧极限之间存在如下关系.

定理1.3　极限的充分必要条件是

图1.11