【摘要】:例如,Sn=xn,x∈[0,1).显然{Sn}在[0,1)上点态收敛于S=0.0<ε<1,要使∣Sn-S∣=xn<ε,必须,因此可取而因此,{Sn}在[0,1)上不一致收敛于S.3){Sn}在D上不一致收敛于S是指:ε0>0,N>0,n0>N和x′∈D,使得,记为.
1)函数列{Sn(x)}在D上(点态)收敛于S(x)是指:∀x0∈D,数列{Sn(x0)}收敛于S(x0).用ε—N的语言表示就是:∀ε>0,∃N=N(ε,x0)>0,当n>N时,成立
∣Sn(x0)-S(x0)∣<ε.
我们通常说的“函数列在D上收敛”就是指的“点态收敛”.
2)函数列{Sn(x)}在D上一致收敛于S(x)是指:∀ε>0,∃N=N(ε)>0,
当n>N时,∀x∈D,恒成立
∣Sn(x)-S(x)∣<ε.
记为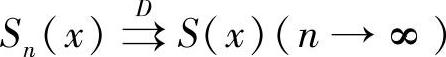 .
.
若对∀[α,β]⊂D,都有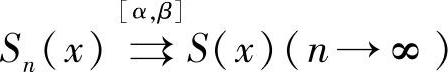 ,则称{Sn(x)}在D上内闭一致收敛.(https://www.xing528.com)
,则称{Sn(x)}在D上内闭一致收敛.(https://www.xing528.com)
一致收敛是整体概念(像函数在[a,b]上一致连续一样),而点态收敛是局部概念(像函数的连续性、可导性一样).因此,由函数列在D上内闭一致收敛并不能得到函数列在D上一致收敛.反之是可以的.
从定义上看,点态收敛的N与x0有关,而一致收敛的N与x0无关,它适用于D中一切x.因此,点态收敛能否成为一致收敛的关键是: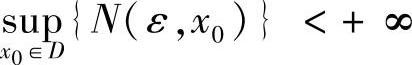 是否成立?
是否成立?
例如,Sn(x)=xn,x∈[0,1).显然{Sn(x)}在[0,1)上点态收敛于S(x)=0.∀0<ε<1,要使∣Sn(x)-S(x)∣=xn<ε,必须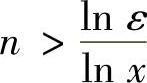 ,因此可取
,因此可取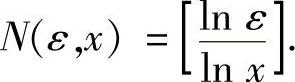
而
因此,{Sn(x)}在[0,1)上不一致收敛于S(x).
3){Sn(x)}在D上不一致收敛于S(x)是指:∃ε0>0,∀N>0,∃n0>N和x′∈D,使得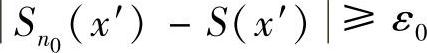 ,记为
,记为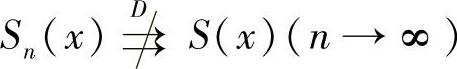 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




