精选名校真题：定积分性质及应用

定积分的性质很多，大致可分为四类：第一类，积分的线性性；第二类，积分区间的可加性；第三类，积分的单调性；第四类，积分的中值性.对于第一积分中值定理，同学们比较熟悉，不再赘述，下面将第二积分中值定理笔之于后，至于它的证明可参看相关《数学分析》教材.

第二积分中值定理

（1）若函数f（x）在[a，b]上单调减少、非负，函数g（x）在[a，b]上可积，则∃ξ∈[a，b]，使得

（2）若函数f（x）在[a，b]上单调增加、非负，函数g（x）在[a，b]上可积，则∃ξ∈[a，b]，使得

（3）若函数f（x）在[a，b]上单调，函数g（x）在[a，b]上可积，则∃ξ∈[a，b]，使得

例4.28　设F₀（x）=lnx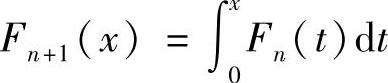，，n=0，1，2，…，x>0.求极限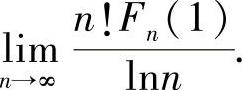

解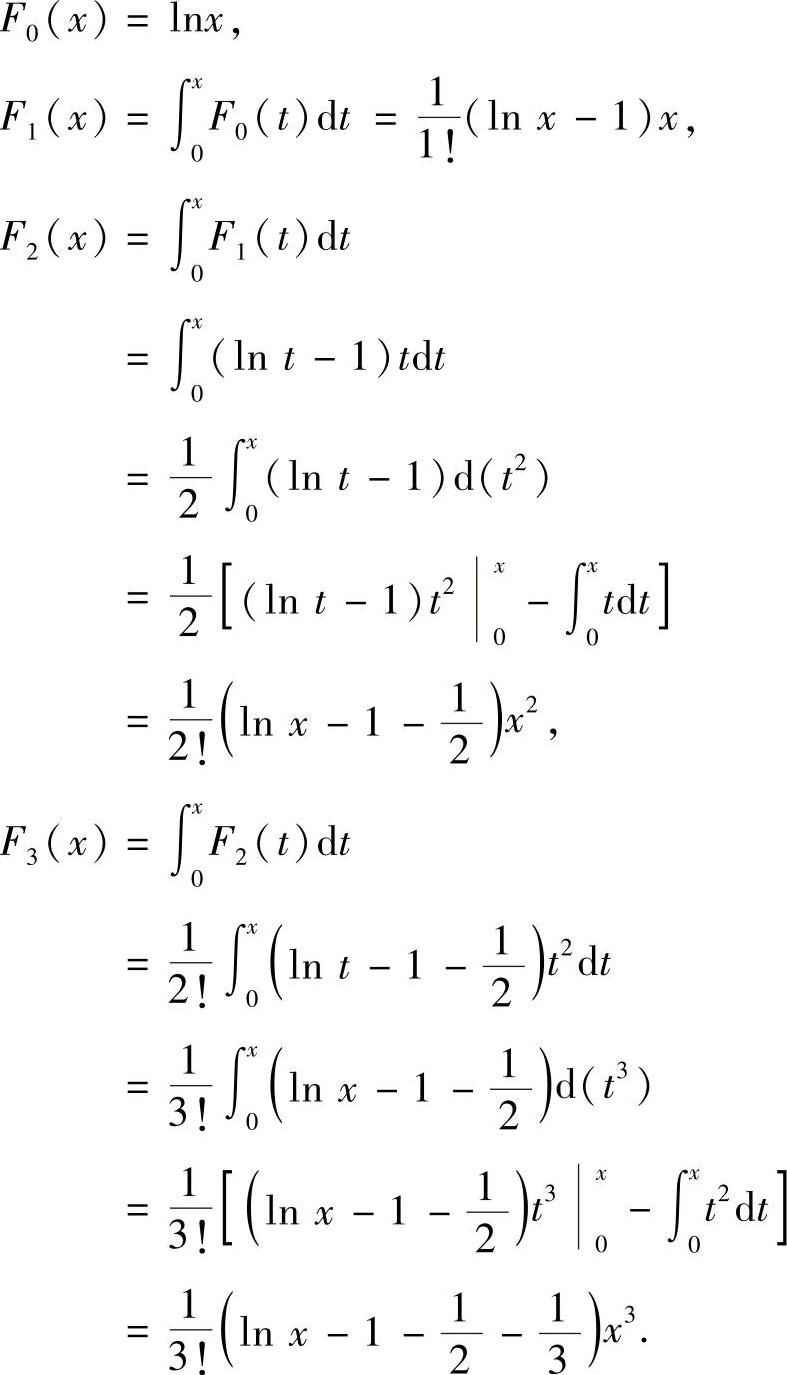

用数学归纳法，不难证明：

于是，由施图兹定理可得

例4.29 证明：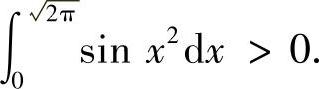

证明 令t=x²，则，，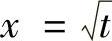

对上式右端第二个积分，作变换t=π+u，则有

故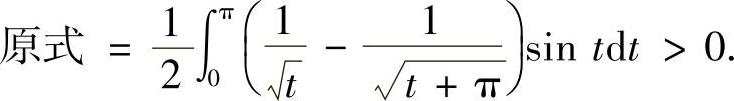

这里注意到了在（0，π]上，sint>0.

类题1 不计算积分，判断下列积分的符号.

类题2 选择题：设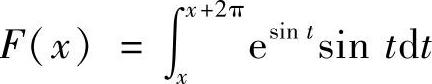，则F（x）的值（ ）.

（A）为正常数； （B）为负常数；

（C）恒为零； （D）不为常数.

（数学Ⅱ）

例4.30　设f（x），g（x）是[a，b]上的正值连续函数，求证：

（复旦大学）.

证明　设f（x）在[a，b]上的最大值为M，且在点ξ取到，即f（ξ）=M.∀ε>0，∃δ>0，使∀x∈[ξ-δ，ξ+δ]∩[a，b]=[α，β]有

f（ξ）-ε<f（x）≤f（ξ）.两边n次方，并乘以g（x）有

[f（ξ）-ε]ⁿg（x）<[f（x）]ⁿg（x）≤[f（ξ）]ⁿg（x）.

在[α，β]上积分，再开n次方，有

进而，有

注意到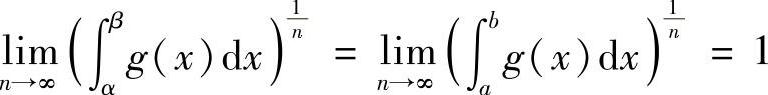，可得

由ε>0的任意性，可知结论成立.

这个例题有如下的变形.

类题1 设f在[a，b]上连续，且f（x）≥0，证明：

提示 设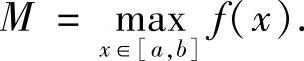分M≡0和M>0两种情况讨论.

类题2 设f，g是[a，b]上的连续函数，且f（x）>0，g（x）≥0，求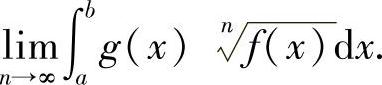

提示 设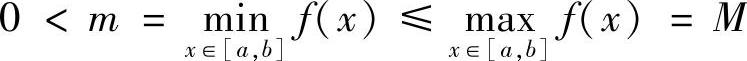，则有

由此易知，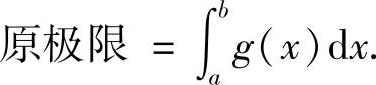

类题3 设f（x）在[a，b]上连续，且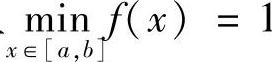.证明：

提示 这是例4.30的特殊情形.在例4.30中取g（x）≡1，f（x）用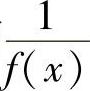替代.

类题4 设f（x）是[α，α+1]上的连续正值函数，记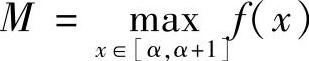.证明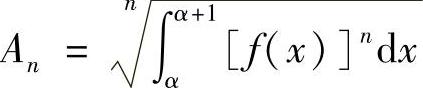：关于n单调递增，且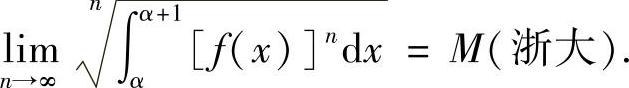

提示 只证明{A_n}关于n单调递增.取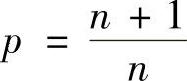，q=n+1，显然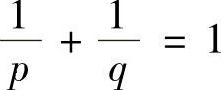.由Hölder不等式，有

即{A_n}关于n单调递增.

例4.31 若函数f（x），g（x）在[a，b]上取正值且连续，记

则数列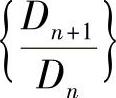收敛，且

证明 这里我们将用到如下

命题 设{a_n}是正数列，则

其详细证明可参见参考文献[2].

设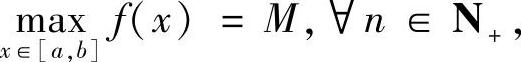

即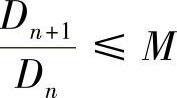，这表明数列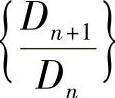有上界.

由柯西-施瓦茨不等式，有

即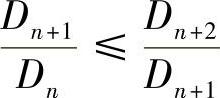，这表明数列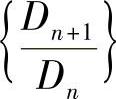单调增加.

由单调有界定理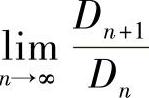，存在，再由命题及上例的结果有

例4.32 设f（x）在[-1，1]上连续，证明：

证明 直接对进行计算是不容易的，因此可考虑用第一积分中值定理将f（x）提到积分号外边.

其中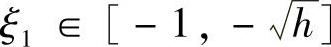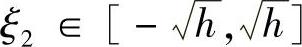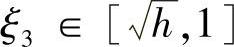，，，h>0适当小.

由于f（x）在[-1，1]上连续，所以f（x）有界，设f（x）≤M.于是有

综上有

本例是“核”积分的极限问题（积分核为“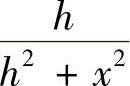”），下例也属于这类问题.但由于f（x）的条件较弱，不能应用第一积分中值定理，因此，我们将给出另外一种作法，这两种作法均是处理“核”积分极限问题的有效方法.

例4.33　设f（x）在[-1，1]上可积，且在点x=0处连续.设

证明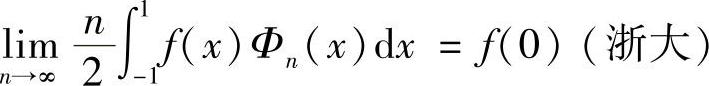：.(https://www.xing528.com)

证明　因为f（x）在[-1，1]上可积，所以f（x）在[-1，1]上有界，设界为M，即∣f（x）∣≤M，∀x∈[-1，1].

又因为f（x）在x=0处连续，所以∀ε>0，∃δ>0，当x∈（-δ，δ）时，有

∣f（x）-f（0）∣<ε.通过计算易知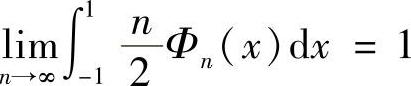，因此，欲证结论成立，只需证

为此，将积分分为三段进行估计：

而

综上可知，原结论成立.

类题1　设f（x）在[a，b]上可积，并是在x=b处连续，证明：

提示　因为f（x）在[a，b]上可积，所以存在M>0，使得f（x）≤M，∀x∈[a，b].

又由f（x）在x=b处连续可知，∀ε>0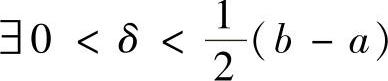，，当x∈（b-δ，b）时，有

f（x）-f（b）<ε.

注意到

我们有

类题2　设f（x）≥0在（-∞，+∞）上连续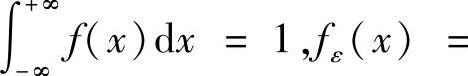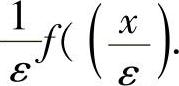，试证明：对每一个有界连续函数φ（x），有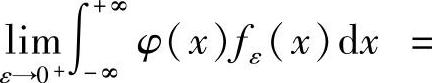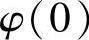（华南理工）.

提示　由已知条件，存在M>0，使得|φ（x）|≤M，∀x∈（-∞，+∞）及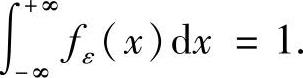再由φ（x）的连续性，对∀σ>0，∃δ>0，当x∈（-δ，δ）时，有|φ（x）-φ（0）|<σ.于是，有

注意到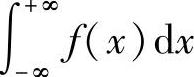，收敛，我们有.

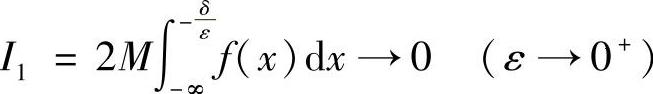同理I₃→0（ε→0+）.而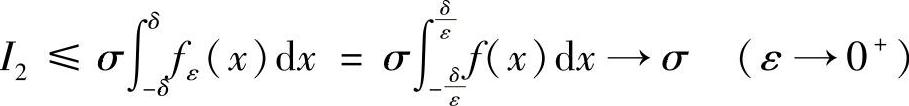.由σ的任意性，可知结论成立.

例4.34　（黎曼引理）设f（x）在[a，b]上可积，证明

证明　对任意的有限区间[α，β]，有

因为f（x）在[a，b]上可积，所以它有界，设f（x）≤A.∀ε>0，由f在[a，b]上的可积性知，存在[a，b]的分割T：a=x₀<x₁<…<x_n=b，使得

于是，当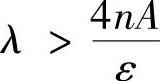时，有

故

同理可证另一个等式.

利用黎曼引理可十分简便地求出下面的极限，请同学们试之.

黎曼引理有下面的一般形式.

推广的黎曼引理　设f（x）在[a，b]上可积，g（x）是以T为周期的周期函数，且在[0，T]上可积，则

由于证明比较复杂，在此我们省略.

类题1　设S（x）=4[x]-2[2x]+1，f（x）在[0，1]上可积，证明：

证明　易知S（x）是以1为周期的函数，且当x∈[0，1]时，

显然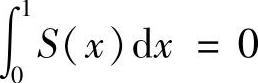，由推广的黎曼引理知

类题2　设f（x）在[0，π]上连续，求证

取g（x）=∣sinx∣，它是以π为周期的函数，且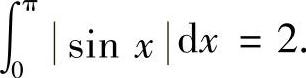由推广的黎曼引理可知，结论成立.

下面我们不用推广的黎曼引理，直接证明.

证明　∣sinnx∣以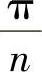为周期.将[0，π]n等分，即

记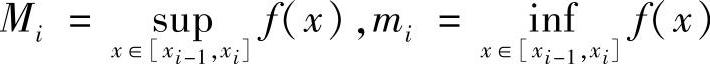，则

这里利用第一积分中值定理，并注意到了f（x）的可积性.

例4.35　证明定积分的连续性：设函数f（x）和f_h（x）=f（x+h）在[a，b]上可积，则有

证明　∀ε>0，取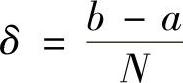，N∈N₊.取_n>N，作[a，b]的n等分，其分点为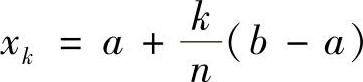，k=0，1，…，n.由f的可积性，有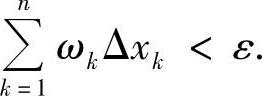

当0<h<δ时，∀x∈[x_k-1，x_k]，有

sup∣f（x+h）-f（x）∣≤ω_k+ωk+1.

从而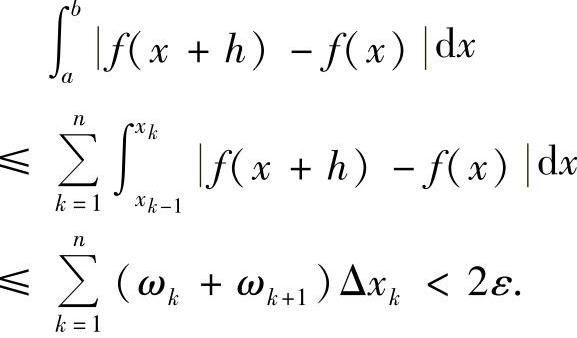

当-δ<h<0时，可类似地证明.

例4.36　证明：当m<2时，

证明　当m≤0时，结论显然成立.

当m>0时，这是一个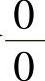型的不定式.使用洛必达法则，可证当m<1时，结论成立，但当1≤m<2时，洛必达法则失效.

下面用第二积分中值定理来证明.

令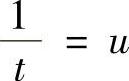，则

因为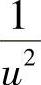为非负递减函数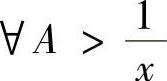，，由第二积分中值定理，有

所以

当m<2时，由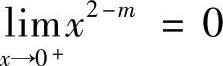知，原结论成立.

例4.37　证明

证明　分部积分，有

类题1　设f″（x）在[0，1]上连续，求证：

类题2　求证：

提示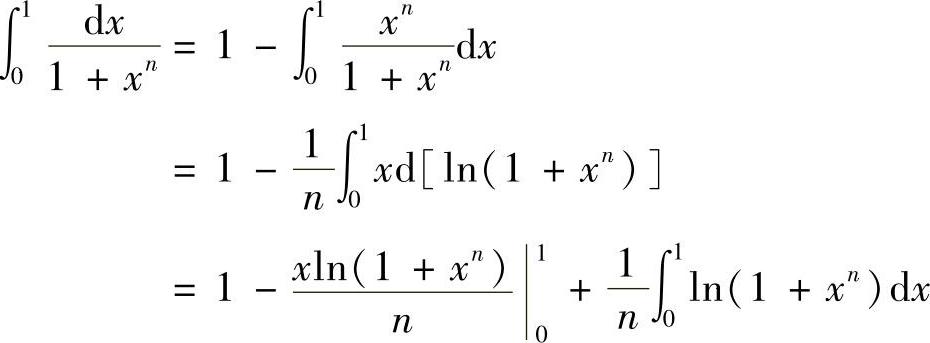

余下的只需证明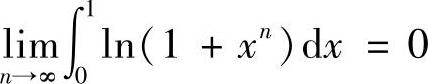即可，请同学们自行完成.