斯托克斯公式及应用-考研数学分析总复习：精选名校真题

斯托克斯公式是将空间曲面上的第二型曲面积分与该曲面边界上的第二型曲线积分之间建立联系的重要公式.

设Σ是空间分片光滑曲面，Σ的边界L由分段光滑曲线组成.又设P，Q，R在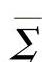上具有一阶连续偏导数，则

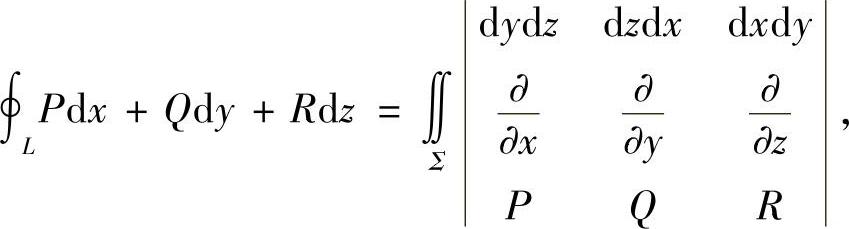
其中L的方向与Σ的方向符合右手法则.

或

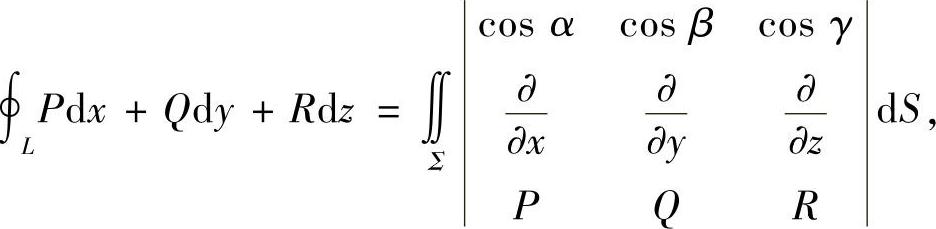
其中cosα，cosβ，cosγ是Σ的法向量的方向余弦.

若Σ是xy平面上的区域，则上两式就变成了格林公式.

由斯托克斯公式很容易推出R³中的曲线积分与路径无关的条件：设Σ是R³中的曲面单连通区域，u=Pdx+Qdy+Rdz，其中P，Q，R在Σ内有连续偏导数，则下列结论等价：

（1）对Σ内任一闭曲线C，有；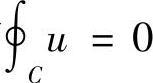

（2）对Σ内任一路径C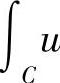，仅与C的起点、终点有关，而与所走的路径无关；

（3）在Σ内成立

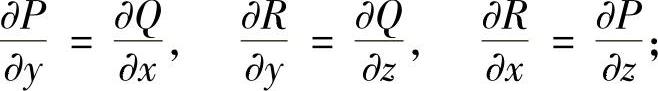
（4）存在函数W（x，y，z），使得在Σ内成立

dW=Pdx+Qdy+Rdz，

且

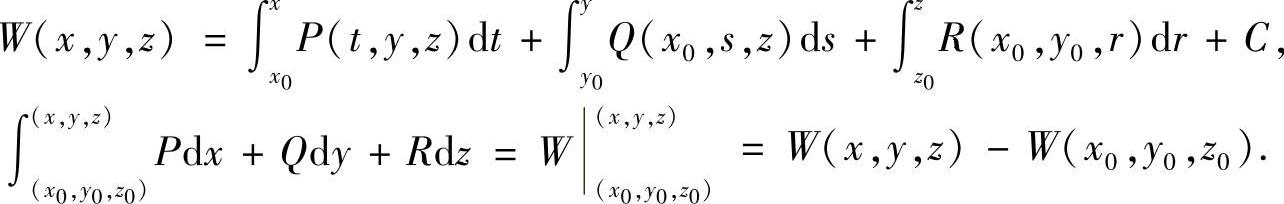
例7.61 选择题：设S：x²+y²+z²=a²（z≥0），S₁为S在第一卦限中的部分，则有（ ）（数学Ⅱ）.

解　因为曲面S关于yOz、zOx平面对称，所以由对称性定理有

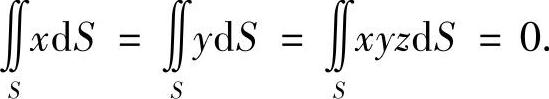
而

故应选（C）.

例7.62　设S是椭圆面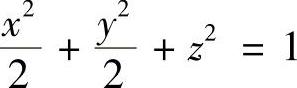的上半部分，点P（x，y，z）∈S，Π为S在点P的切平面，ρ（x，y，z）为点O（0，0，0）到平面Π的距离，求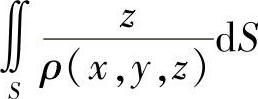（数学Ⅱ）.

解　设（X，Y，Z）为Π上任意一点，则Π的方程为

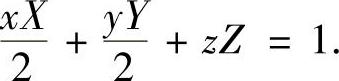
由此易知

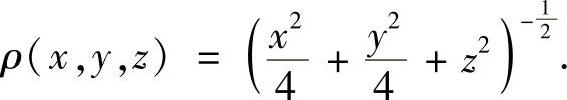
由S的方程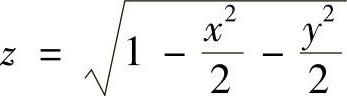有，

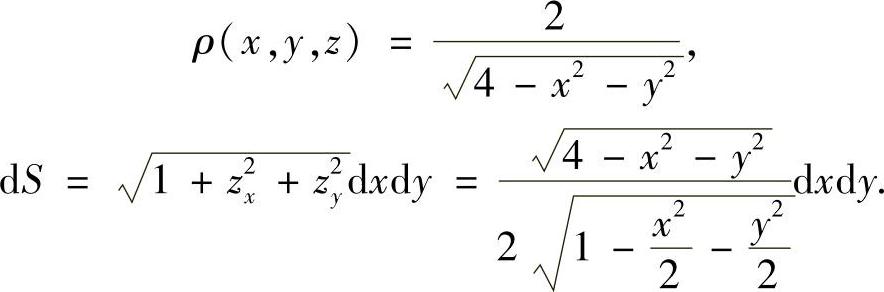
于是

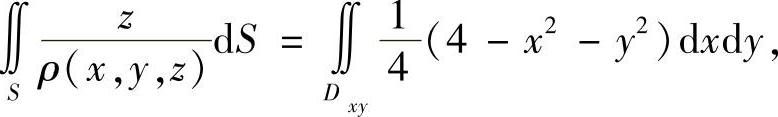
其中D_xy：x²+y²≤2是S在xOy平面上的投影.

作极坐标变换容易求出：

例7.63　计算曲面积分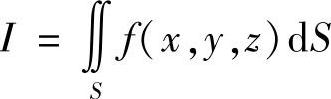，其中

S是球面x²+y²+z²=1.

解　将球面S分成三部分S₁，S₂，S₃，其中

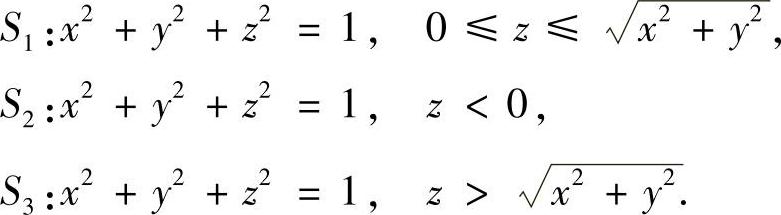
此时

曲面S₁在xOy平面的投影区域为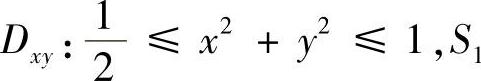的方程为z=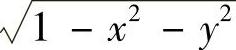，故有

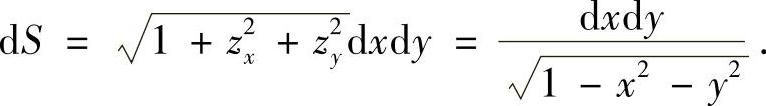
从而

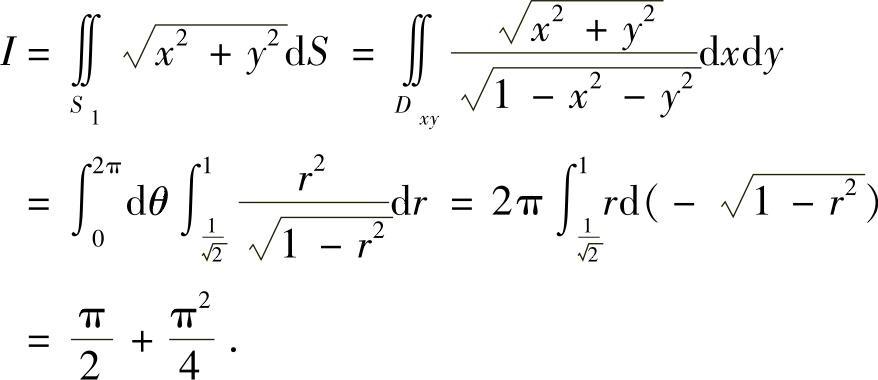
类题　计算积分

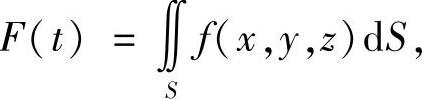
其中 S：x²+y²+z²=t²，

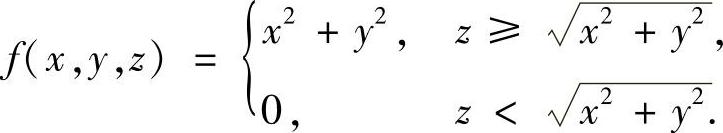
答案：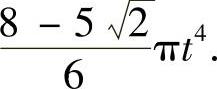

例7.64　计算积分

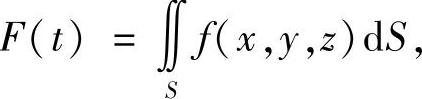
其中 S：x+y+z=t，

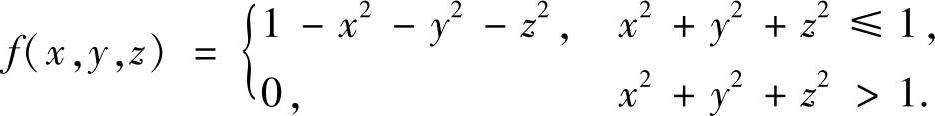
分析　首先必须搞清楚：t取何值时，f≠0；t又取何值时，f=0.也就是说，t取何值时平面S与球有交；t取何值时平面S与球无交.

解　将z=t-x-y代入x²+y²+z²≤1整理可得：

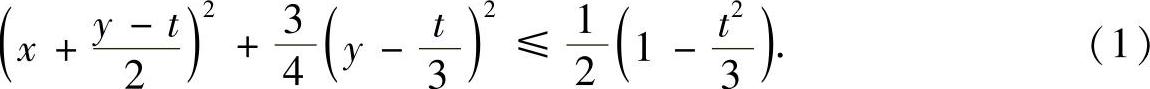
由此可知，当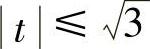时，平面S在球x²+y²+z²=1内；当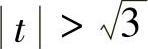时，平面S在球x²+y²+z²=1之外，所以

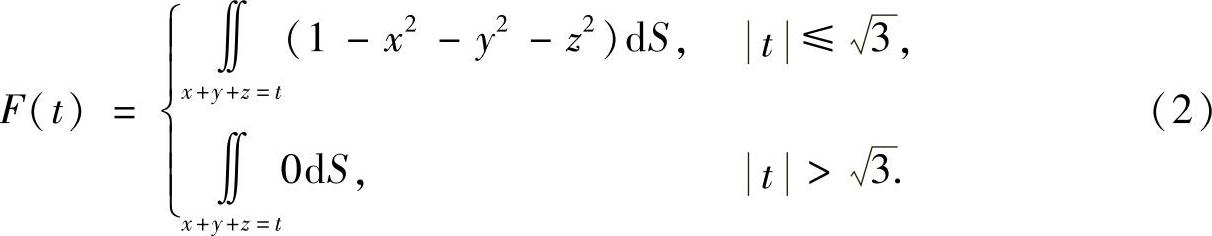
显然当_t>3时，F（t）=0，所以只需计算t≤3时的积分：

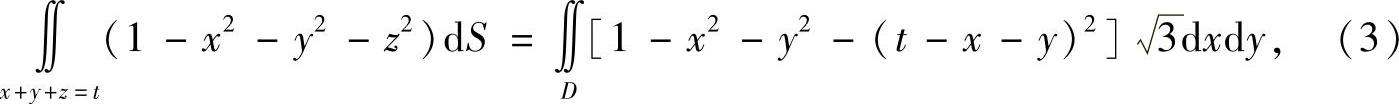
其中D是式（1）所表示的区域.作变换

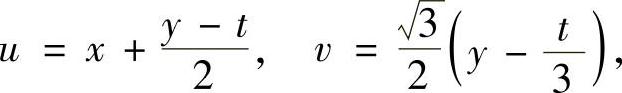
则D变为D′：u²+v²≤ρ²，其中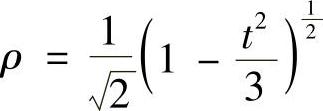.于是

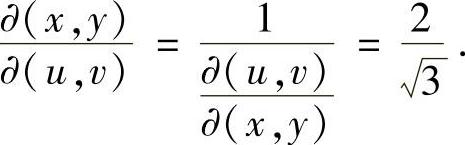
对式（3）右边进一步计算得

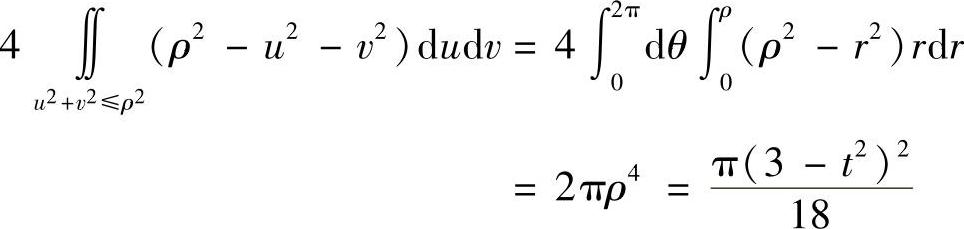
所以

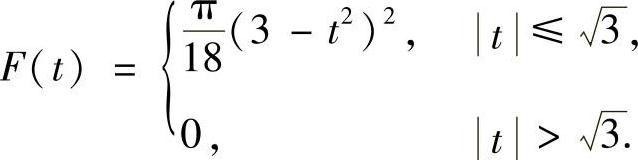
例7.65　计算积分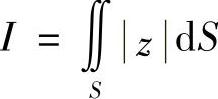，其中S为柱体x²+y²≤ax被球体x²+y²+z²≤a²截取部分的表面积.

解　用S₁表示S在第一卦限部分，用S₁₁和S₁₂分别表示S₁的柱面和球面部分.由对称性，有

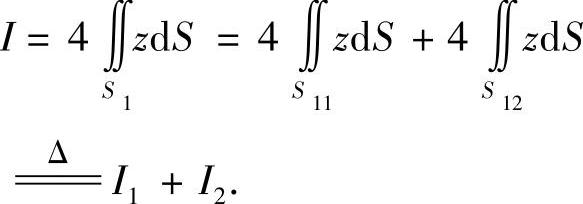
球面与柱面的交线方程为

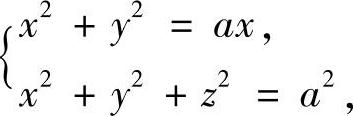
从中消去y，可得S₁₁在xOz平面上的投影区域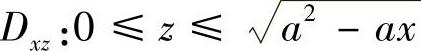，0≤x≤a.由S₁₁的方程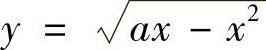可得

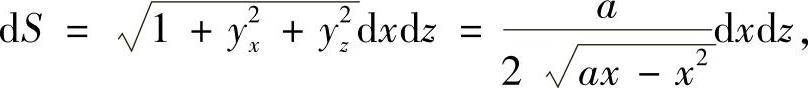
故

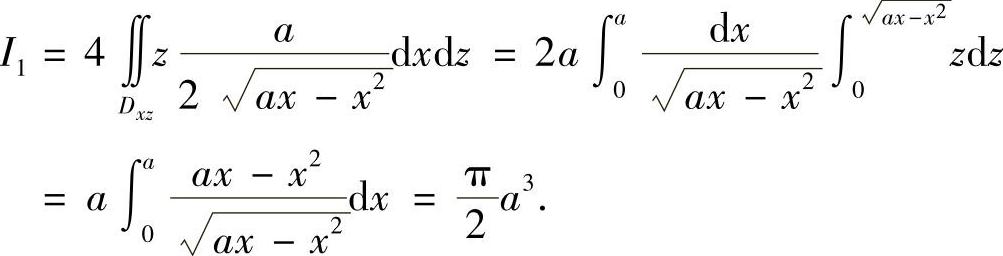
S₁₂在xOy平面上的投影区域D_xy：x²+y²≤ax，y≥0.

由S₁₂方程为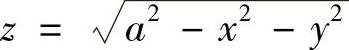可得

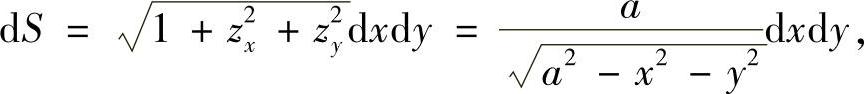
故

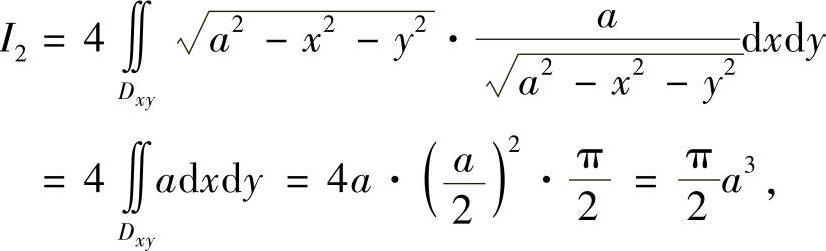
从而

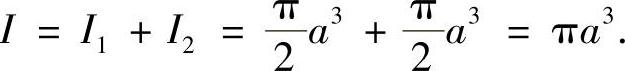
类题　计算积分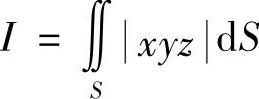，其中

（1）S为x+y+z=1；

（2）S为抛物面z=x²+y²被z=1割下的部分.

答案：（1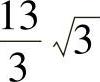）；（2）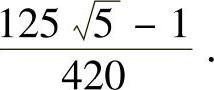

例7.66 设曲面S由方程（x²+y²+z²）2=x²-y²所确定，求曲面S的面积.

解 在球坐标变换：x=rsinφcosθ，y=rsinφsinθ，z=rcosφ之下，曲面S的方程是r²=sin²φcos2θ，其参数方程为

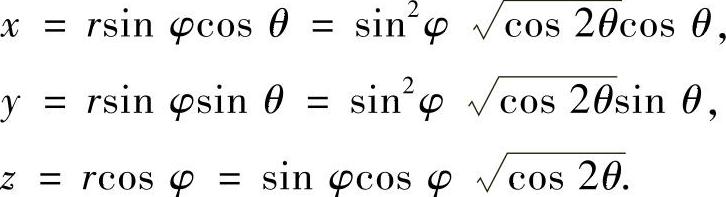
通过计算易知，

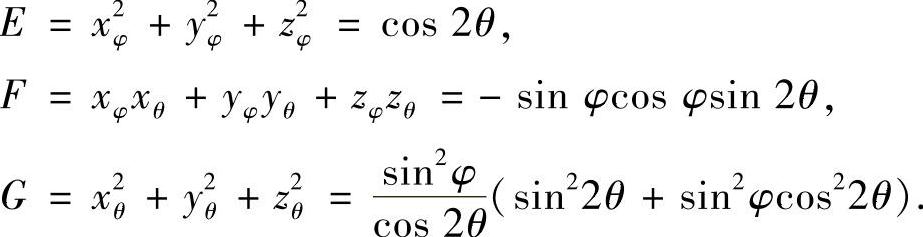
由此得

EG-F²=sin⁴φ.

由曲面的对称性，只需求第一卦限部分的面积即可.而此时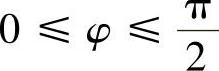，并且由曲面方程知cos2θ≥0，所以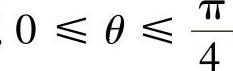.故S的面积为

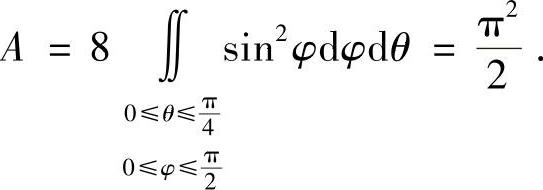
例7.67 证明泊松（Poisson）公式

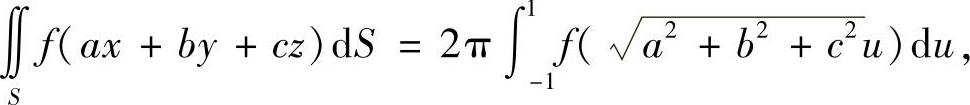
其中S是球面x²+y²+z²=1（南开；川大）.

证明 若a=b=c=0，则结论显然成立.

若a，b，c不全为零，记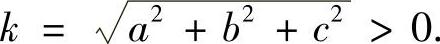把单位向量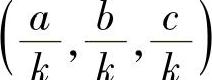扩充成正交阵

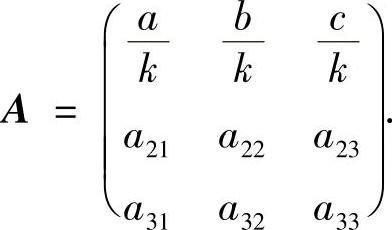
作正交变换

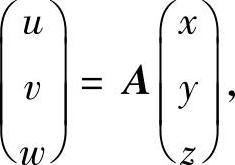
则变换的雅可比行列式

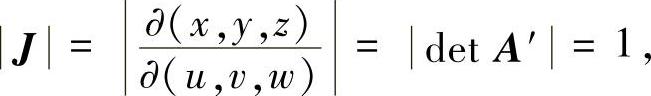
球面S变成了球面S′：u²+v²+w²=1，即

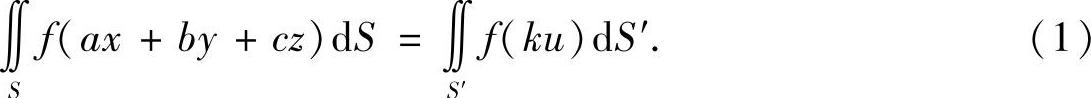
对球面S′上的积分作变换：

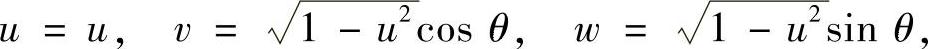
-1≤u≤1，　0≤θ≤2π.

通过计算可知，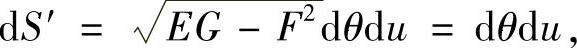

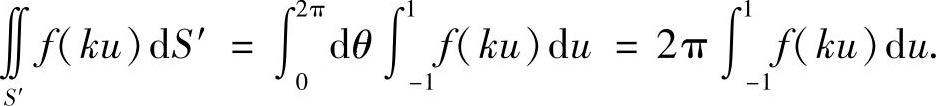
由式（1）知，结论成立.

注7.11　本例证明过程中的式（1），实际上告诉我们了一个结论：第一类曲面积分在正交变换下具有不变性，即

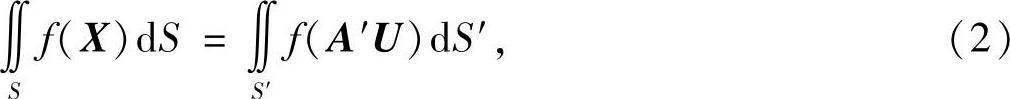
其中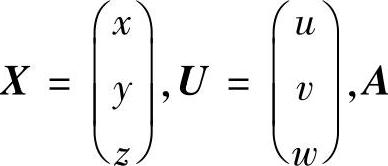是正交阵，满足U=AX，A′是A的转换，曲面S′是曲面S在正交变换下的像.

关于这个一般性结论的证明：先将曲面S表示为参数形式，然后通过正交变换写出S′的参数形式，最后将式（2）两端都化成关于参数的重积分，易见两者相等.

另外，本例的结果在球坐标之下通常写成如下形式：设f（x）连续，则成立

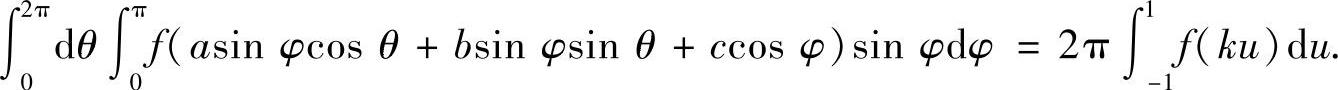
类题1　试证：

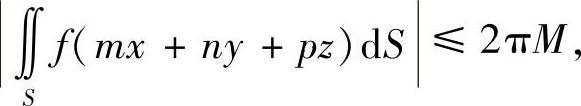
其中m²+n²+p²=1，m，n，p为常数.f（t）在t≤1上连续可微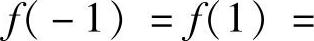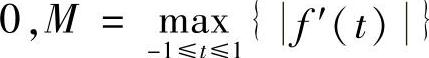，，S表示半径为1，球心在原点的球面（东北工学院）.

提示　应用泊松公式，有(https://www.xing528.com)

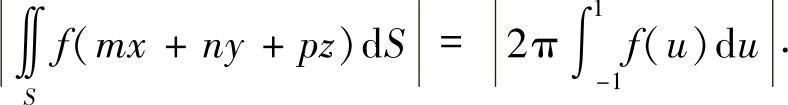
分部积分可知，

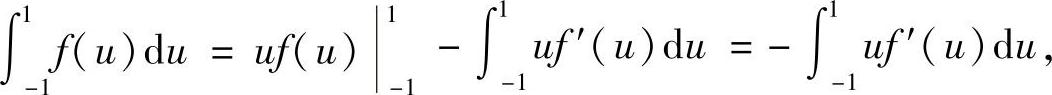
故

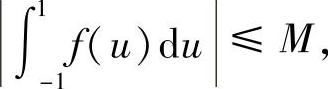
从而原结论成立.

类题2　设f（x）在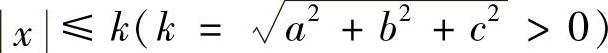上连续，证明

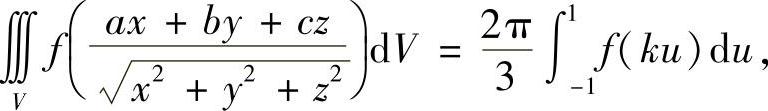
其中V：x²+y²+z²≤1（广西大学）.

提示　对等式左边作球坐标变换，有

例7.68　计算曲面积分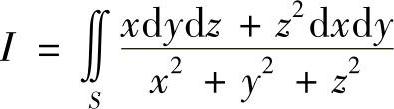，其中S是曲面x²+y²=R²及两个平面z=R，z=-R（R>0）所围的立体的表面的外侧（数学Ⅰ，Ⅱ）.

解　设S₁，S₂，S₃分别为S的上、下底面和圆柱侧面，则

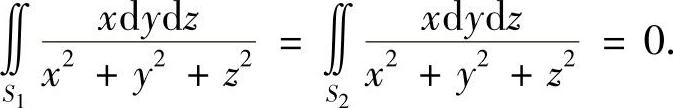
记S₁，S₂在xOy平面上的投影区域为D_xy，则

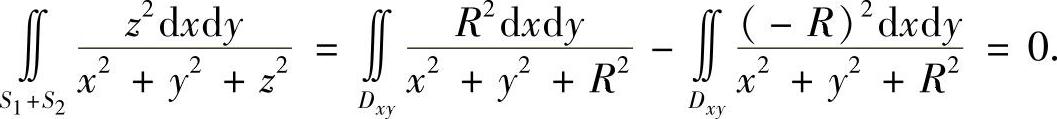
在S₃上，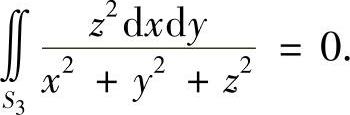

而S₃在yOz平面上的投影区域D_yz：-R≤y≤R，-R≤z≤R，故

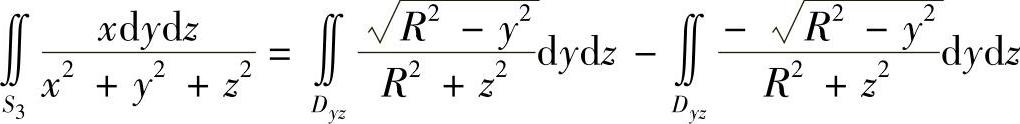
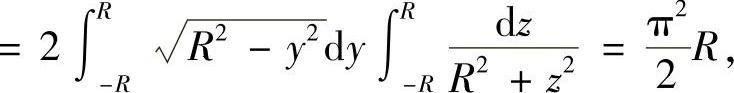
从而曲面积分

注7.12　虽然S是一个封闭曲面，但被积函数在原点处有奇性，因此不能使用高斯公式.这个题目看起来复杂，但仔细观察积分曲面和被积函数的特点会立即发现，有五个积分都是零，需要我们计算的实际上只有一个积分.

例7.69　计算曲面积分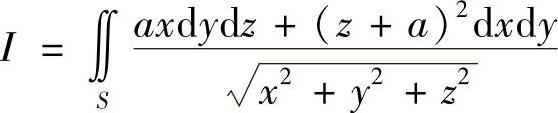，其中S为下半球面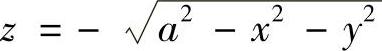的上侧，a>0为常数（数学Ⅰ）.

解　采用补面法.按常规应补平面S₁：x²+y²≤a²，z=0.仔细观察发现被积函数在原点处有奇性，不能直接应用高斯公式，但注意到在下半球面上的点（x，y，z）满足x²+y²+z²=a²，则可将原曲面积分改写成

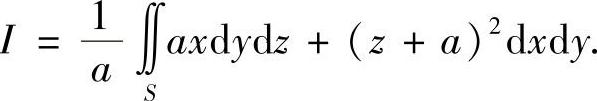
这样，取S₁的法向方向与z轴正向相反，就可对上式使用高斯公式了.于是有

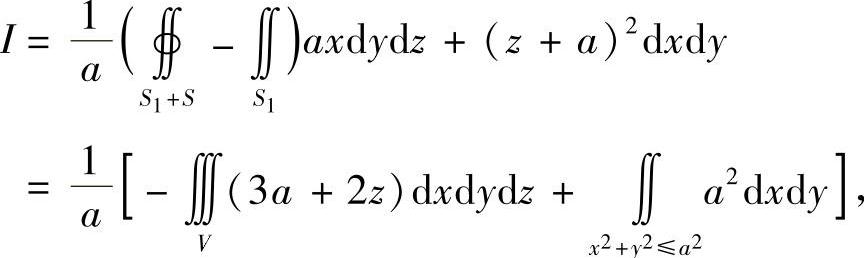
其中V是S₁，S所围的空间区域.故

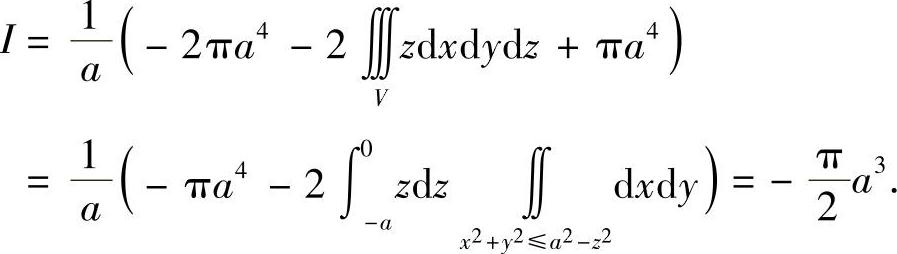
类题　计算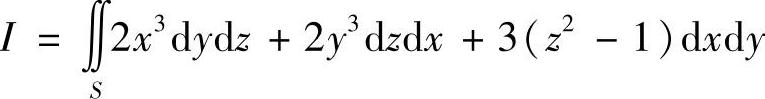，其中S是z=1-x²-y²，（z≥0）的上侧（数学Ⅰ）.

提示　补面S₁：x²+y²≤1，z=0，方向取下侧.用高斯公式易知I=-π.

例7.70　计算曲面积分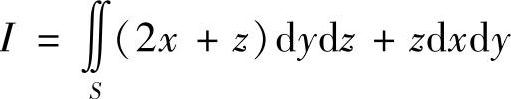，其中S为有向曲面z=x²+y²（0≤z≤1），其法向量与z轴正向的夹角为锐角（数学Ⅰ，Ⅱ）.

解法1（用高斯公式求解）.用S₁表示法向量指向z轴负方向的有向平面z=1（x²+y²≤1），D_xy表示S₁在xOy平面上的投影区域，即

D_xy：x²+y²≤1.

于是

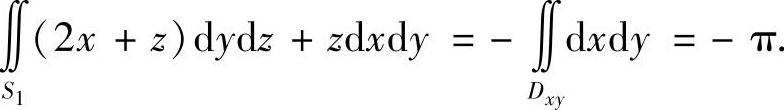
记Ω为S和S₁所围成的空间区域，则由高斯公式有

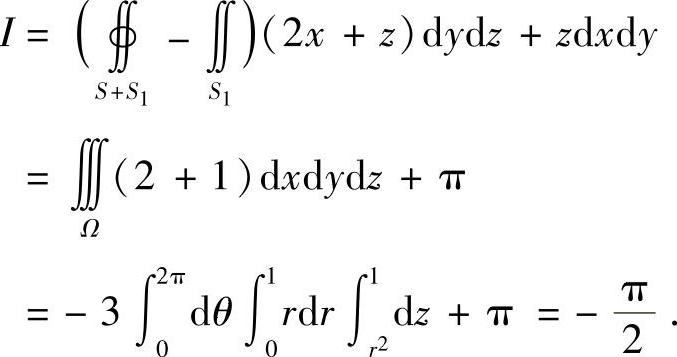
解法2　（用两类曲面积分的关系求解）　用D_xy表示S在xOy平面上的投影区域.曲面z=x²+y²的法向量为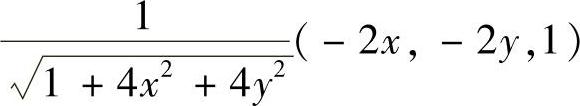，所以

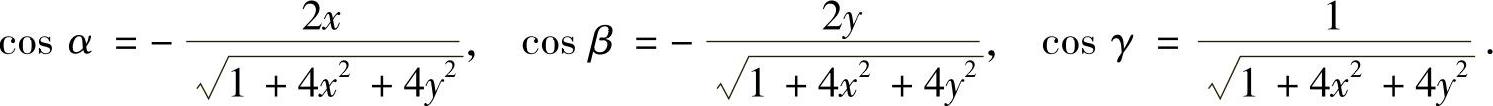
于是

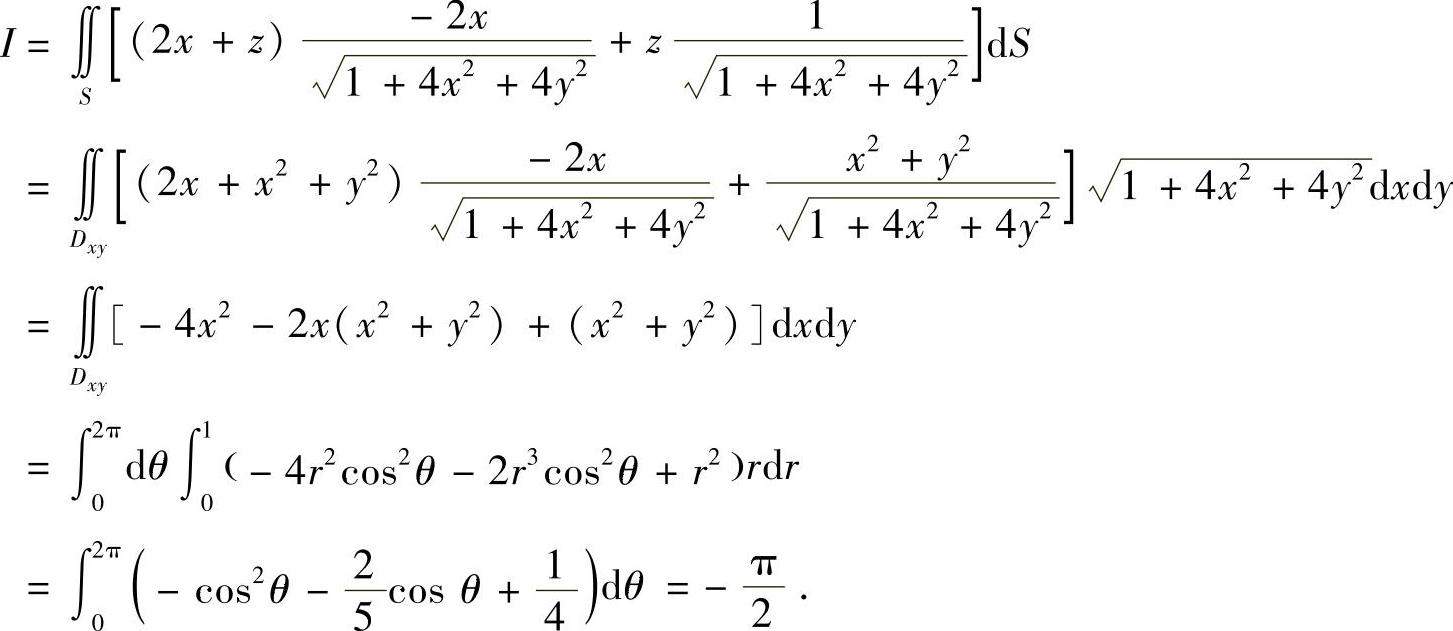
另外，这个题也可直接求解.

例7.71　求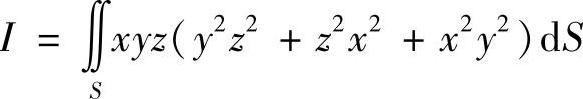，其中S是球面x²+y²+z²=a2（x≥0，y≥0，z≥0）的第一卦限部分，取外侧.

解　球面在点（x，y，z）处的法向量为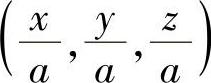，由两类曲面积分的关系，有

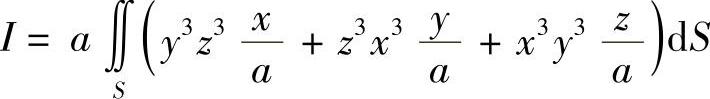
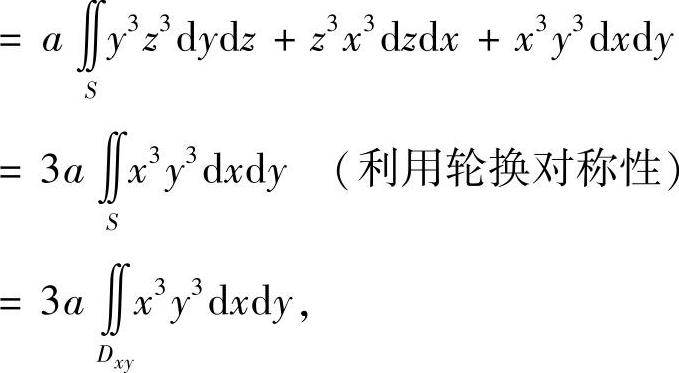
其中D_xy：x²+y²≤a²，x≥0，y≥0.作极坐标变换，有

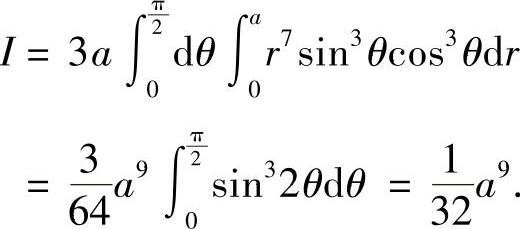
例7.72　计算曲线积分

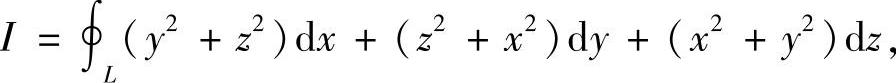
L是x²+y²+z²=2r₁x与x²+y²=2r₂x的交线（0<r₂<r₁，z>0），L的方向是使L所围的球面上较小部分区域保持在左边.

解　由于球面的外法向的方向余弦为

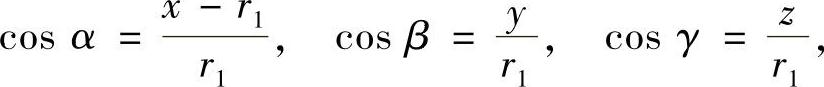
所以由斯托克斯公式，有

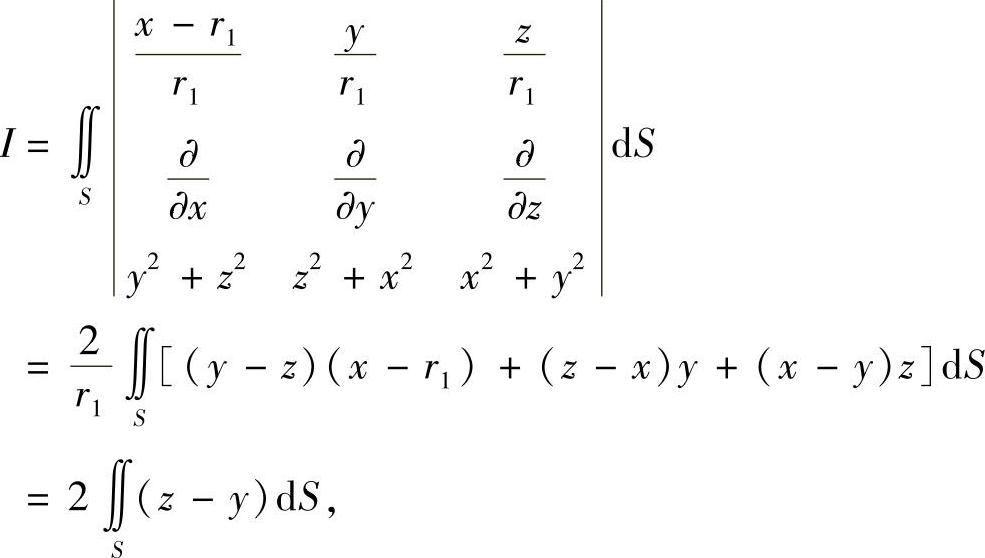
其中S是球面x²+y²+z²=2r₁x由L所围的部分.

由于曲面S关于xOz平面对称，所以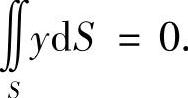又由

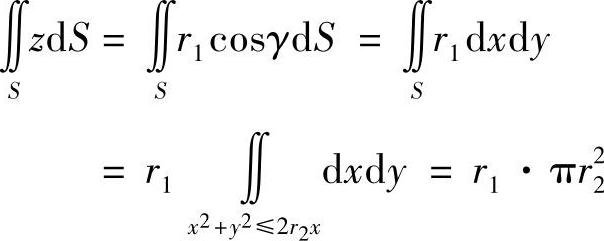
可知，

I=2πr₁r²_2.

注7.13　本例亦可用参数方程求解，但非常复杂.具体说来，先将L用参数方程表示：

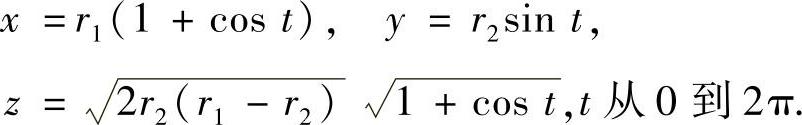
则有

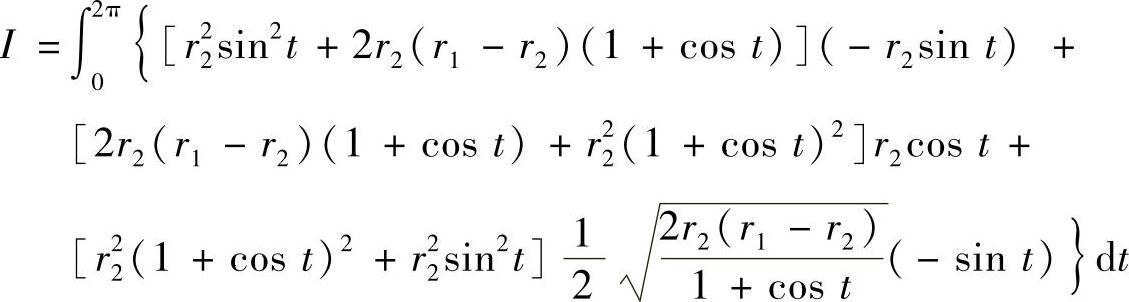
有兴趣的同学可以尝试一下，完成本题.

例7.73　计算曲面积分

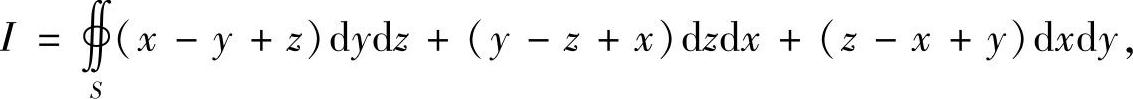
S是闭曲面∣x-y+z∣+∣y-z+x∣+∣z-x+y∣=1，方向取外侧.

解　由高斯公式，可得

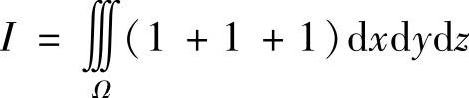
其中Ω是由闭曲面S所围的空间区域.

作变换：u=x-y+z，v=y-z+x，w=z-x+y，则

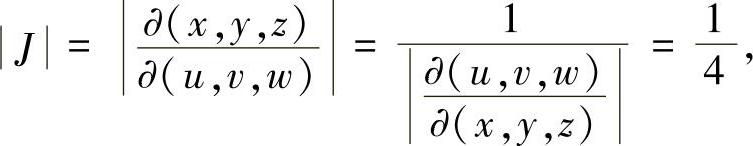
区域Ω变成Ω′：∣u∣+∣v∣+∣w∣≤1.由对称性，有

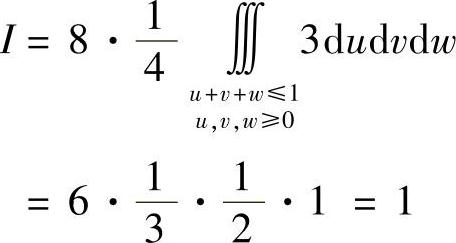
类题　计算曲面积分

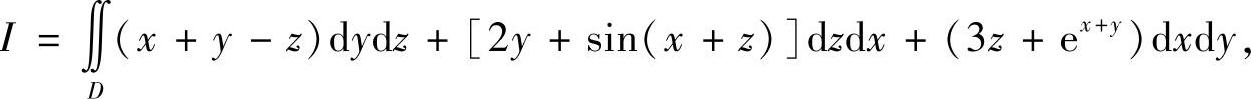
其中S是曲面∣x-y+z∣+∣y-z+x∣+∣z-x+y∣=1的外表面（武大）.

答案　I=2.

例7.74　计算第二型曲面积分

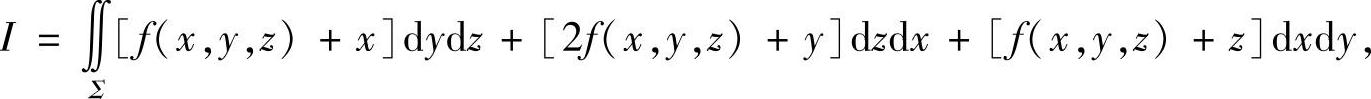
其中f（x，y，z）为连续函数，Σ是平面x-y+z=1在第四卦限部分，方向取上侧.

分析　即使补充三个坐标平面使之与Σ一起构成封闭曲面，但由于f的光滑性不够，我们仍然无法使用高斯公式.下面采用所谓的“归一化”方法，将“未知”的f消去.

解　设曲面Σ的单位法向量为（cosα，cosβ，cosγ），则dydz=cosαdS，dzdx=cosβdS，dxdy=cosγdS.由此可得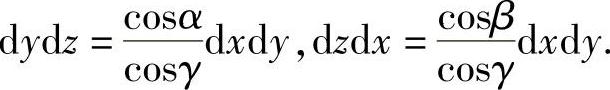

具体到本例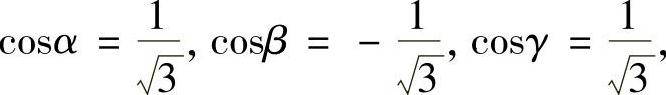，因而dydz=dxdy，dzdx=-dxdy.于是

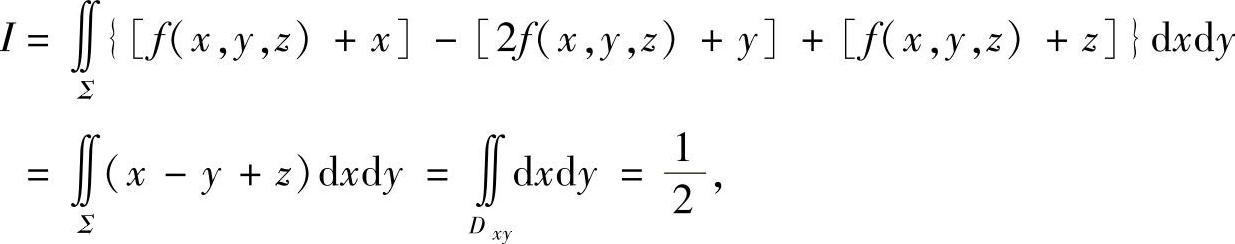
其中D_xy={（x，y）0≤x≤1+y，-1≤y≤0}是曲面Σ在xOy平面的投影.

例7.75　计算曲面积分

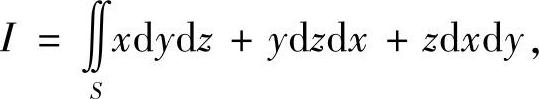
其中S是由下面参数方程所给出的曲面

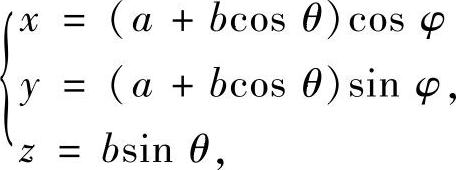
方向取外侧（式中θ，φ为参数，0≤θ≤2π，0≤φ≤2π，a，b为常数，a>b>0）（复旦大学）.

解　计算易知

A=-b（a+bcosθ）cosθcosφ，　B=-b（a+bcosθ）cosθsinφ，

C=-bsinθsinφ（a+bcosθ）（cosφ+sinφ）.

由此可以看出向量（A，B，C）与S的外法向方向相反（例如，考察第一卦限曲面S上任一点处的C值发现C<0，而在该点处的外法向的方向余弦cosγ>0，所以向量（A，B，C）与S的外法向方向相反），故将I化成关于θ，φ的积分后前面取“-”号，即

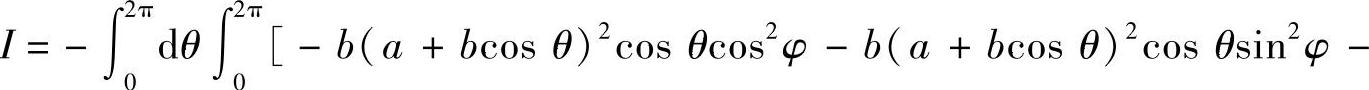
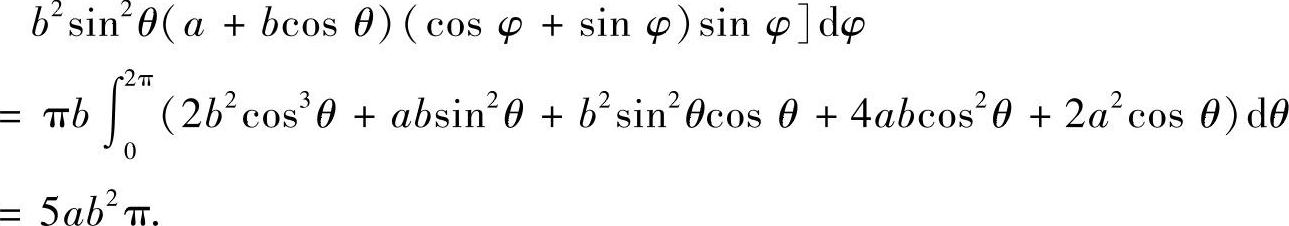
例7.76　计算曲线积分

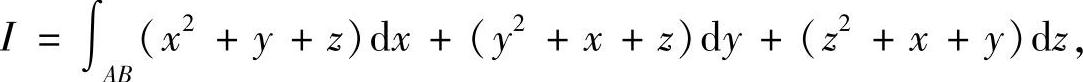
其中A（0，0，0），B（1，1，1）.

解　记P=x²+y+z，Q=y²+x+z，R=z²+x+y.易见，

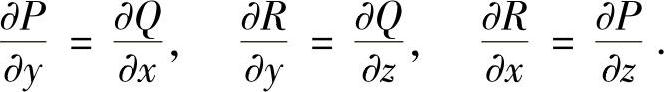
由此知，积分与路径无关.

由

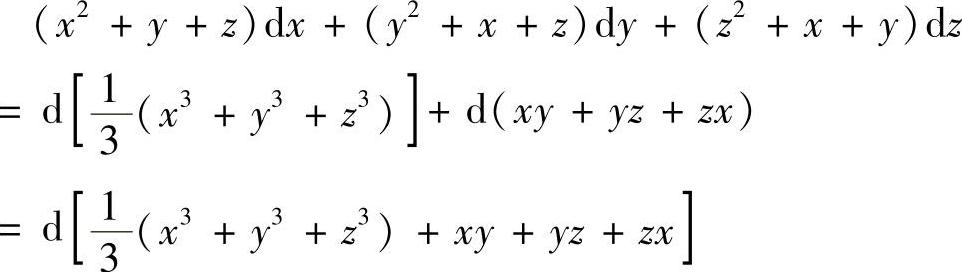
可知，原函数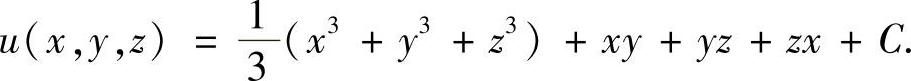故

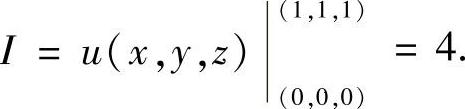
例7.77　设函数φ（y）具有连续导数，在围绕原点的任意分段光滑简单闭曲线L上，曲线积分

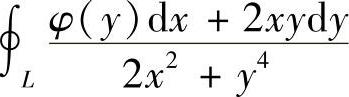
的值恒为同一常数.

（1）证明：对右半平面x>0内的任意分段光滑简单闭曲线C，有

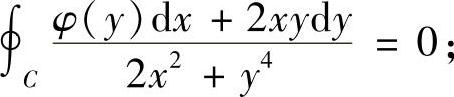
（2）求φ（y）的表达式.

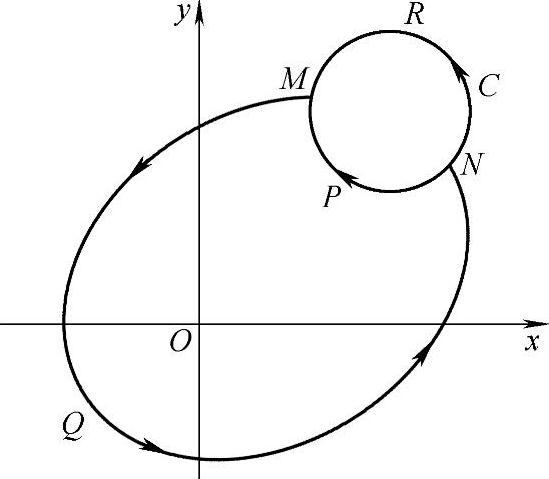
图7-7　例7.77图

证明（1）如图7-7所示，设C是x>0内的任一分段光滑简单闭曲线.在C上任取两点M，N，作围绕原点的闭曲线同时得到了另一条围绕原点的闭曲线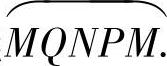由已知条件，有

于是

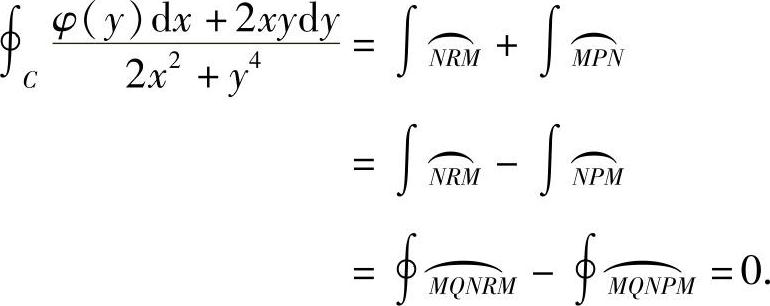
解 （2）记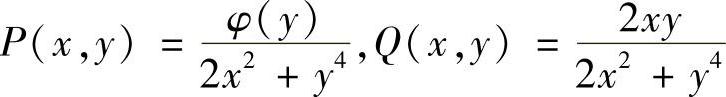，则P，Q在x>0上的单连通区域内有一阶连续编导数，且对任意分段光滑简单闭曲线C，有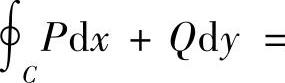0.它的等价条件是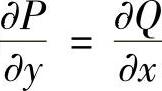，即

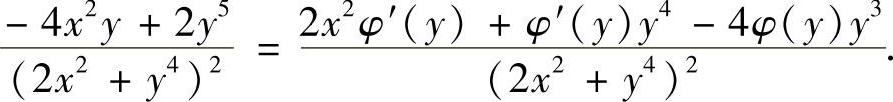
比较上式两边可得

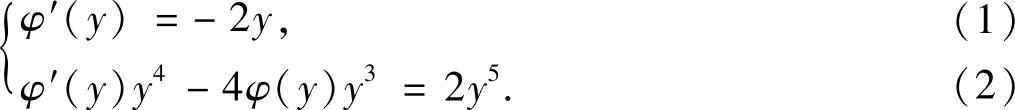
由式（1）得，φ（y）=-y²+c.将其代入式（2）可得c=0，从而φ（y）=-y².