考研数学分析总复习：特殊函数B函数与Γ函数

（1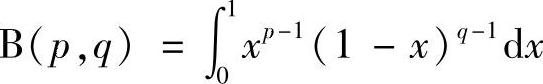），p>0，q>0称为Beta函数或第一类欧拉积分.它的等价形式有：

由此可得

B函数的性质：

1）B（p，q）函数在其定义域p>0，q>0上连续且有任意阶连续偏导数；

2）对称性：B（p，q）=B（q，p）；

3）递推关系式：

如果m，n都是自然数，则

（2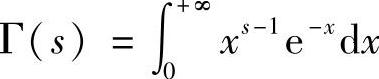），s>0称为Gamma函数或第二类欧拉积分.它的等价形式有：

由此可得

Γ函数的性质：

1）Γ（s）在其定义域s>0上连续，且有任意阶连续导数；

2）递推关系式：Γ（s+1）=sΓ（s），s>0.

如果n是自然数，则

Γ（n+1）=n！；

3）勒让德（Legendre）加倍公式：；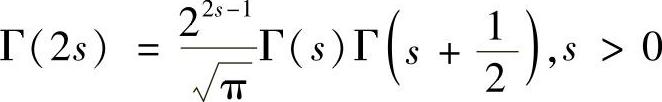

4）余元公式：；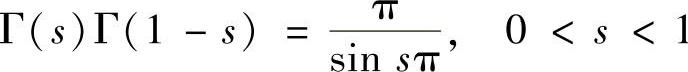

5）与B函数之间的关系

（3）几个重要的积分

例7.20　计算下列积分.

解　（1）令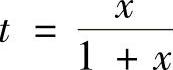，则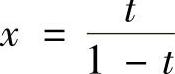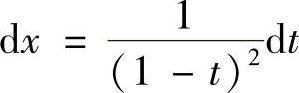，，代入原积分可得(https://www.xing528.com)

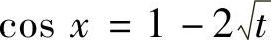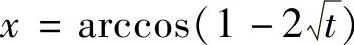（3）令，则，，代入原积分，有

（4）令t=x⁴，则

例7.21 计算下列积分.

解 （1）令x=1-t，则dx=-dt，代入原积分，有

所以

故

对上式右端第一个积分作变换：x=1+t，则

于是有

例7.22 求极限.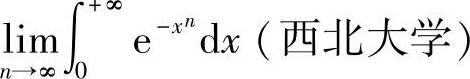

解 这个题目可用含参变量积分的连续性定理解，这里我们用Γ函数来解.

令t=xⁿ，则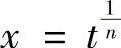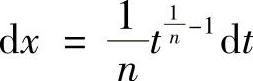，，代入原积分有

这里应用了Γ（s）在其定义域上的连续性.

例7.23 已知0≤h≤1，正整数n≥3，证明：

（中科大）.

证明 令t²=xh²，则，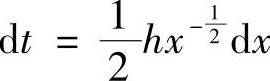

例7.24 设a>0，b>0，c>0，试证：

其中V为四面体，x≥0，y≥0，z≥0，x+y+z=1（郑州大学）.

证明 写出累次积分：

令y=（1-x）t，则