高等数学牛顿-莱布尼茨公式

由定理5.6容易证明下面的重要结论，它给出了在一定条件下，用原函数计算定积分的公式.

定理5.8 若函数f（x）在区间［a，b］上连续，函数F（x）是f（x）在区间［a，b］上的一个原函数，则

公式（5.18）称为牛顿-莱布尼茨公式.

证明 已知函数F（x）是f（x）的一个原函数，因为函数f（x）在区间［a，b］上连续，由定理6知，也是f（x）的一个原函数，所以这两个原函数之间只相差一个常数C，即

Φ（x）=F（x）+C，a≤x≤b

也就是

在上式中令x=a，得到C=-F（a），从而有=F（x）-F（a）.

在上式中令x=b，便得到=F（b）-F（a）.

公式（5.18）进一步揭示了定积分与被积函数的原函数或不定积分之间的联系.它表明一个连续函数的定积分等于被积函数的任一原函数在积分区间［a，b］上的增量.从而把求定积分的问题转化为求原函数即求不定积分的问题，这就给定积分的计算提供了一个有效而又简便的计算方法.(www.xing528.com)

为了方便起见，以后把F（b）-F（a）记为或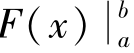，于是式（5.18）又可写为

下面举几个利用公式（5.18）来计算定积分的例子.

例5.8 计算5.1中的定积分

解 由于ex的一个原函数就是ex，所以利用牛顿-莱布尼茨公式，有

例5.9 计算定积分

应用牛顿-莱布尼茨公式必须注意定理的条件，即被积函数f（x）在区间［a，b］上连续.如果被积函数f（x）在区间［a，b］上有有限个第一类间断点，由定积分的充分条件可知，定积分存在.此时可利用定积分关于积分区间的可加性把区间［a，b］分成有限个使函数f（x）保持连续的小区间，在每个小区间上分别计算定积分，然后把结果相加.

解 由于函数f（x）是分段函数，因此Φ（x）的表达式要分段考虑，于是有