Matlab高效解法：一维热传导方程

设函数u(x)在切比雪夫点x=(x₀,x₁,…,x_N)T处的取值为向量u=(u₀,u₁,…,u_N)T。如果诺依曼边界条件仅约束了u′(1)的值（x=-1处为其他边界条件，如狄利克莱边界条件），有：

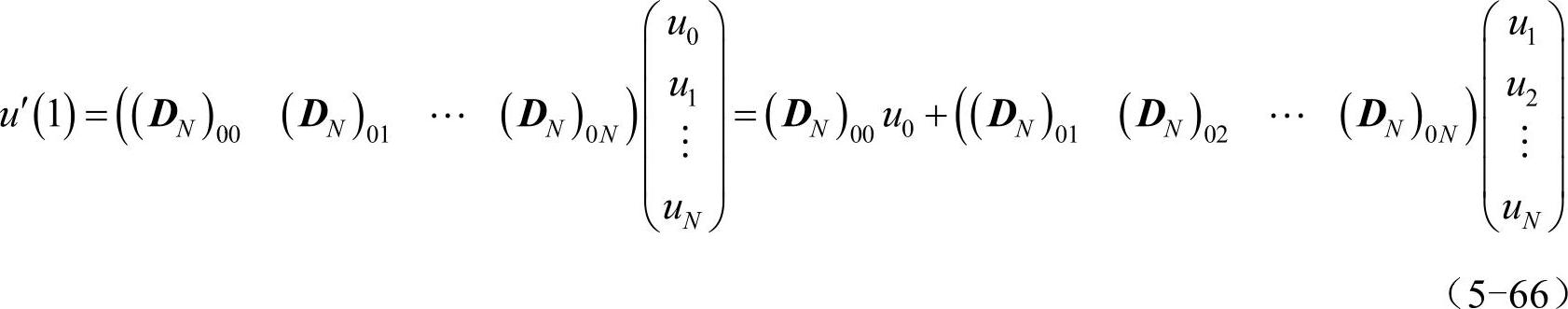
在u′(1)=0的边界条件下，u₀=u(1)与(u₁,u₂,…,u_N)^T的关系为：

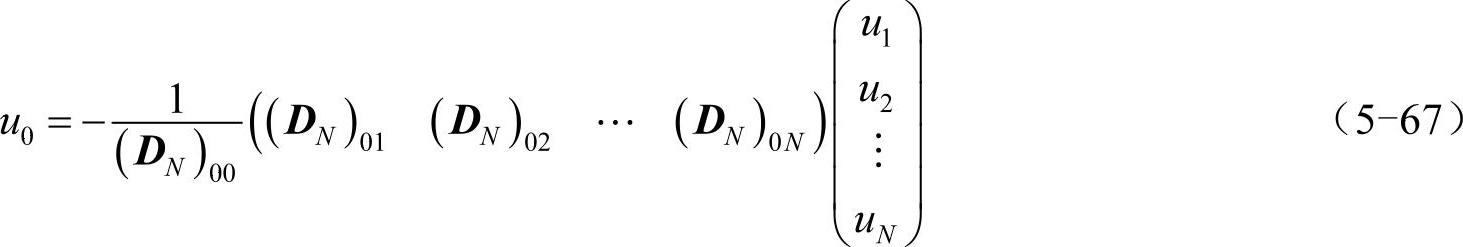
类似地，如果诺依曼边界条件同时约束了u′(±1)的值，有：

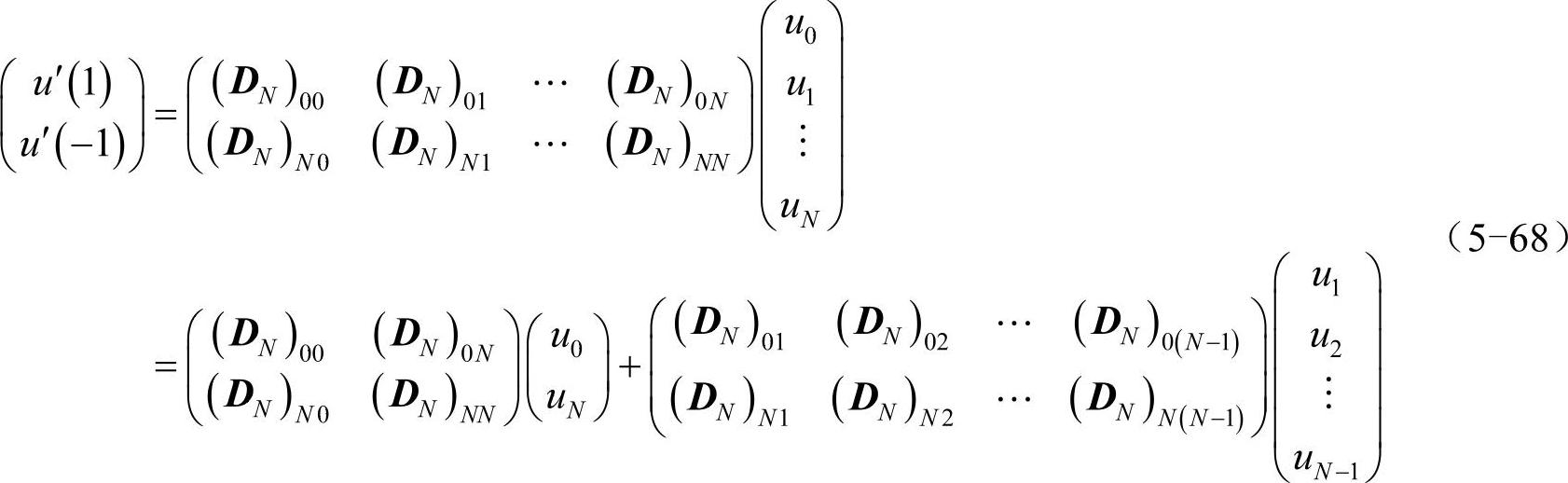
在u′(±1)=0条件下，(u₀,u_N)^T与(u₁,u₂,…,u_N-1)^T关系为：

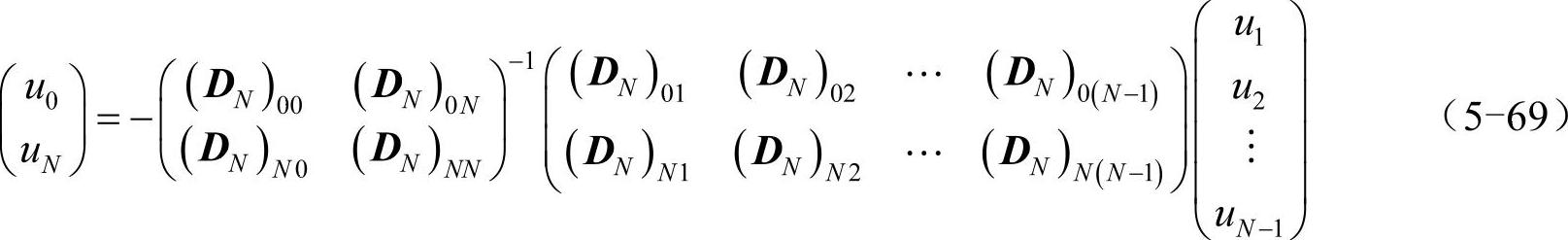
其中，u₀=u(1)，u_N=u(-1)。

式（5-67）和式（5-69）的意义在于：将边界条件u′(1)=0或u′(±1)=0转化为对u(1)或u(±1)的约束条件，这样就可以直接处理单边界或双边界上的诺依曼边界条件了。以一维热传导方程为例：

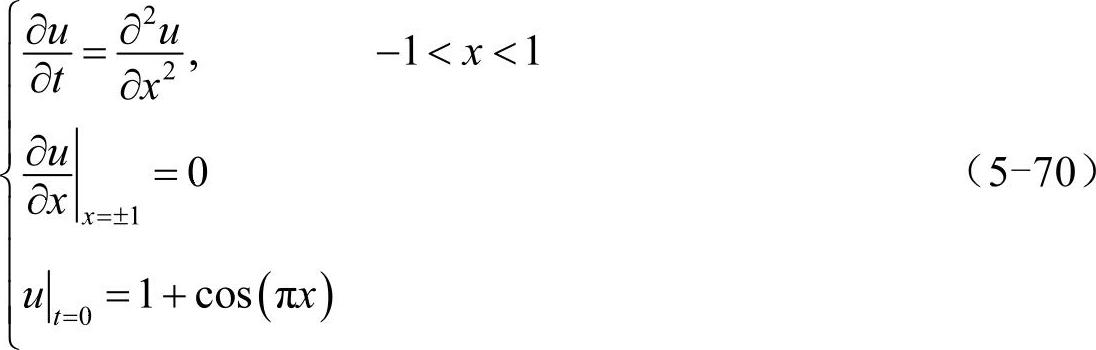
上式描述了均匀细杆上的热传导过程，u代表温度分布，t代表时间，x代表杆上的坐标，诺依曼边界条件∂u/∂x|_x=±1=0代表边界是绝热的。可以预料，若时间t足够长，杆上的温度将处处相等。

容易知道，边界条件可等价写为：

u在边界处的二阶混合偏导数∂(∂u/∂x)/∂t|_x=±1显然是连续的，且由物理意义可知∂u/∂t|_x=±1也是连续的，所以u的二阶混合偏导数的求导次序可以在边界处交换（证明从略）：(https://www.xing528.com)

那么，式（5-70）可等价写为式（5-73）。初始条件已经包含∂u/∂x|_x=±1,t=0=0，这里无需重复。

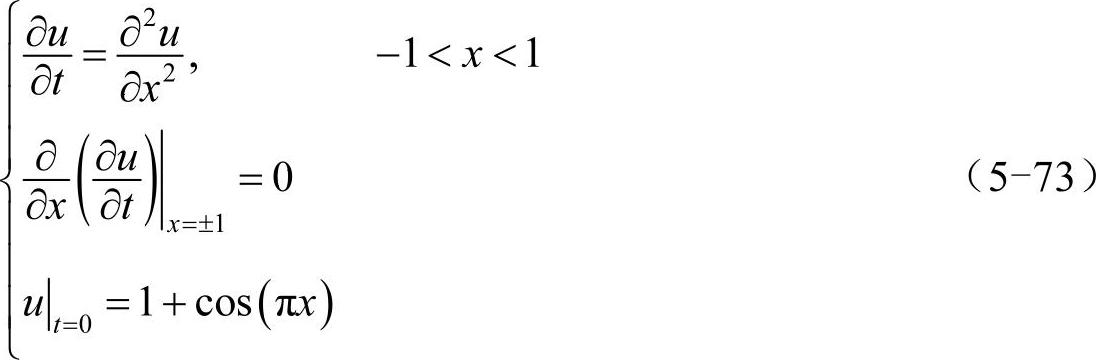
上式中的∂/∂t可用ode45函数计算，∂²/∂x²用矩阵D_N²计算，根据式（5-69）处理诺依曼边界条件（处理时将∂u/∂t看做u），代码如下：

程序5-19

主程序代码如下：

文件heat1D.m代码如下：

输出结果如图5-23所示：t=0时刻杆上的温度分布极不均匀，随着t的增加，热量从高温部分扩散到低温部分，杆上各处温度趋于某一定值。由于两端绝热（∂u/∂x|_x=±1=0），u对x在[-1,1]上的积分结果不随t变化。

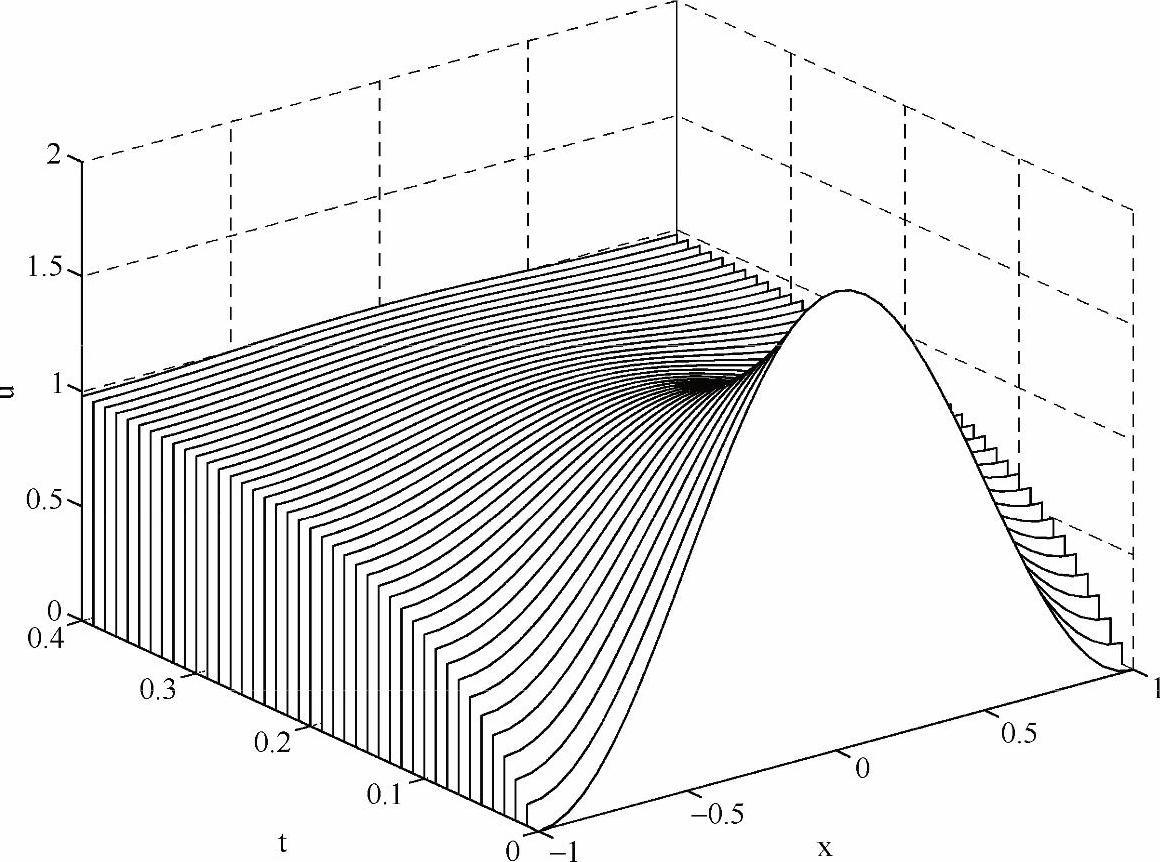
图5-23 两端绝热条件下一维热传导方程的解