根据5.1.1小节,对有限区间内的非周期函数进行数值求导的最佳方法是这样的:首先在计算区间内确定N+1个切比雪夫点x0,x1,…,xN,在这些点上对函数进行代数多项式插值,得到最高次幂小于或等于N的插值函数p(x),然后求插值函数在切比雪夫点处的导数p′(x0),p′(x1),…,p′(xN)。由于上述过程是线性的,可以写成矩阵形式,所以本小节的目标就是总结其中的规律并构造切比雪夫求导矩阵,将求导运算转化为矩阵运算。
选取计算区间为[-1,1],以便讨论。坐标被离散化为xj=cos(jπ/N),其中j=0,1,…,N,用x表示N+1维向量(x0,x1,…,xN)T。与第4章不同,这里的N是任意正整数而不仅是正偶数,区间内的离散点数为N+1个而不是N个,坐标x0,x1,…,xN是由大到小而不是由小到大,请注意区分。用u代表这些位置上的函数值组成的N+1维向量(u0,u1,…,uN)T,p(x)代表它的插值函数。定义DN为(N+1)×(N+1)切比雪夫求导矩阵,并使得下式成立:
p′(x)=DNu (5-5)
先来看N=1和N=2的情况,然后推广到一般情况。N=1时,只有2个插值点x0=1和x1=-1,以及相应的2个函数值u0和u1,则插值函数为:

对其求导,得:

为了满足式(5-5),构造2×2切比雪夫求导矩阵D1为:

N=2时,有3个插值点x0=1、x1=0和x2=-1,以及相应的3个函数值u0、u1和u2,则插值函数为:
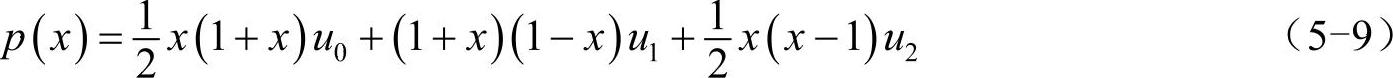
对其求导,得:
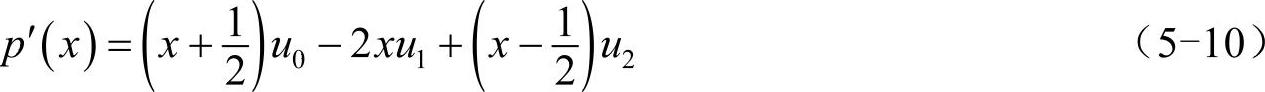
代入x0=1、x1=0和x2=-1就可以得到该位置的导数值。根据式(5-5),3×3切比雪夫求导矩阵D2为:

若继续如此计算更高阶的DN,将会找到其中的规律。下面略过这个过程,直接给出对于任意N的切比雪夫求导矩阵DN中每个元素的表达式:
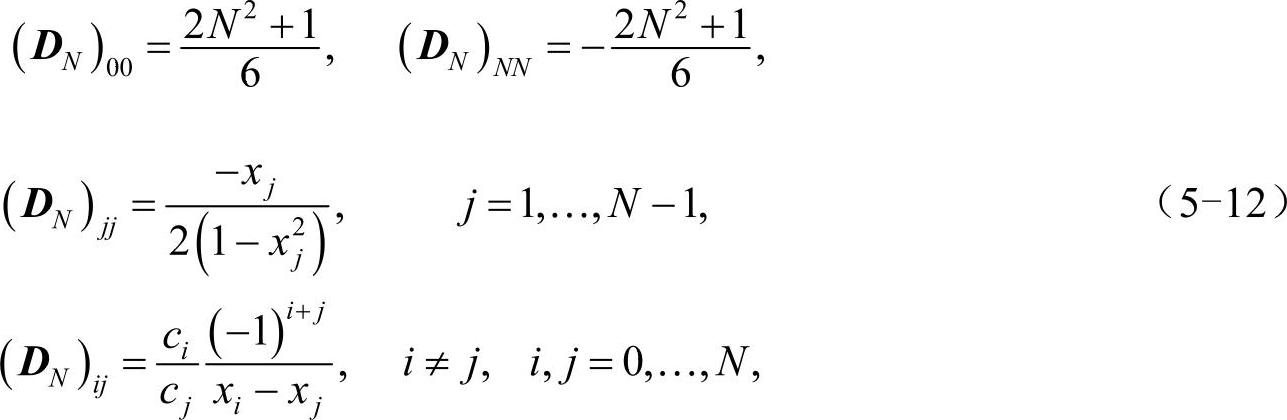
其中(DN)ij代表切比雪夫求导矩阵DN中第i+1行第j+1列的元素。且:

下式直观地给出了切比雪夫求导矩阵DN的结构:

由于后面的程序将反复用到切比雪夫求导矩阵DN和相应的切比雪夫点,所以下面给出函数cheb的定义文件cheb.m,只需输入N的值就能返回DN和相应的切比雪夫点,以便其他程序调用。
程序5-3
cheb.m文件代码如下:
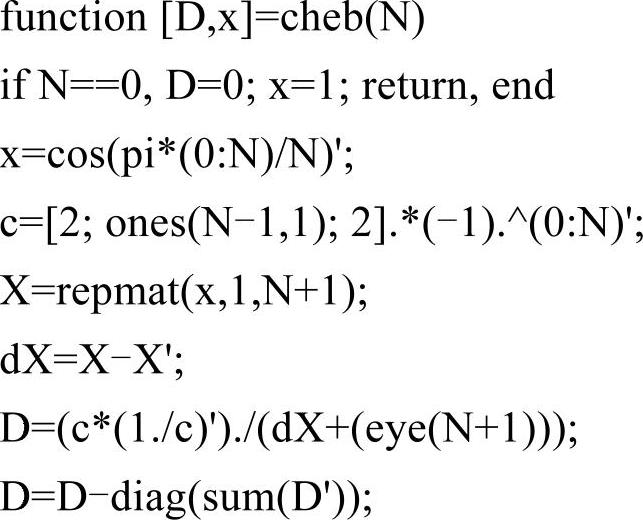
实际上,cheb.m并不是严格按照式(5-12)来计算DN的,对角线上的元素是由对角线以外的元素来计算的,即:(https://www.xing528.com)

这样就给出了存在舍入误差的情况下更具稳定性的DN。试想这个情形:对于离散函数值u=(1,1,…,1)T,它的插值函数为一常数p(x)=1,所以p′(x)=0。这就要求DN与(1,1,…,1)T的乘积必须是(0,0,…,0)T,于是就得到了式(5-15)。
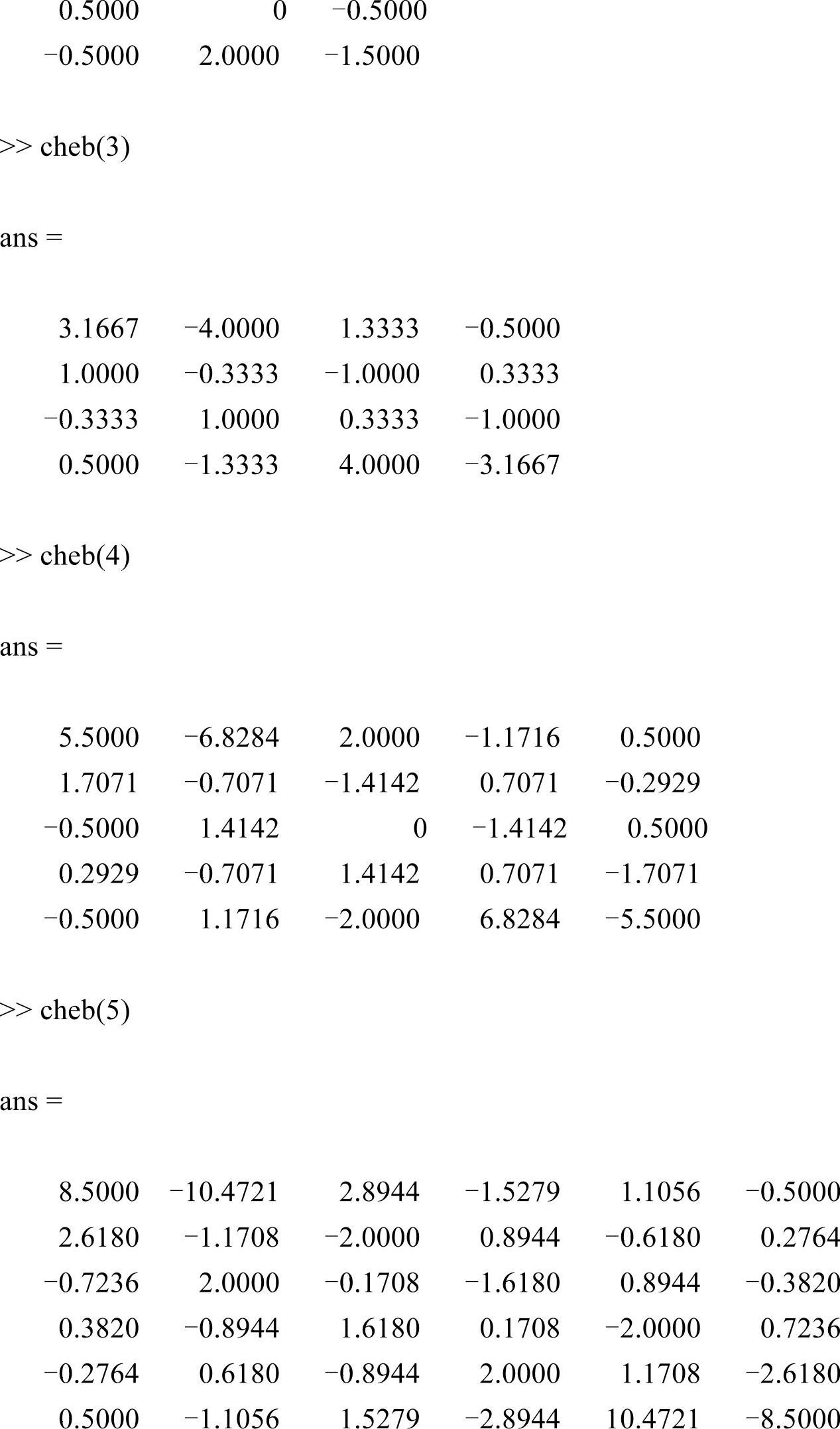
下面是N=1,2,3,4,5时cheb输出的结果,注意到DN是“中心对称”的,即:(DN)ij=-(DN)N-i,N-j。

DN是用于求1阶导数的切比雪夫求导矩阵,要得到用于求2阶导数的切比雪夫求导矩阵,一般有两种思路:(1)用精确的表达式计算。(2)直接对DN平方。为了简便,本书采用第2种思路,同样,还可以得到用于求高阶导数的切比雪夫求导矩阵:

因为DN的表达式是在区间[-1,1]上得到的,所以,在对其他区间上的函数求导前,还需要对DN进行缩放,即:∂/∂x→(2/L)DN,∂n/∂xn→[(2/L)DN]n。
下面的代码用切比雪夫求导矩阵计算u(x)=sech(x)和u(x)=esin(2x)在[-1,1]上的1、2阶导数,并与精确解进行比较。
程序5-4


程序输出结果如图5-4所示,曲线为精确的u(x)、u′(x)和u″(x),点分别为u(xj)及利用切比雪夫求导矩阵计算得到的u′(xj)和u″(xj)。可以看到,在N=32的条件下,误差在10-10至10-14数量级。
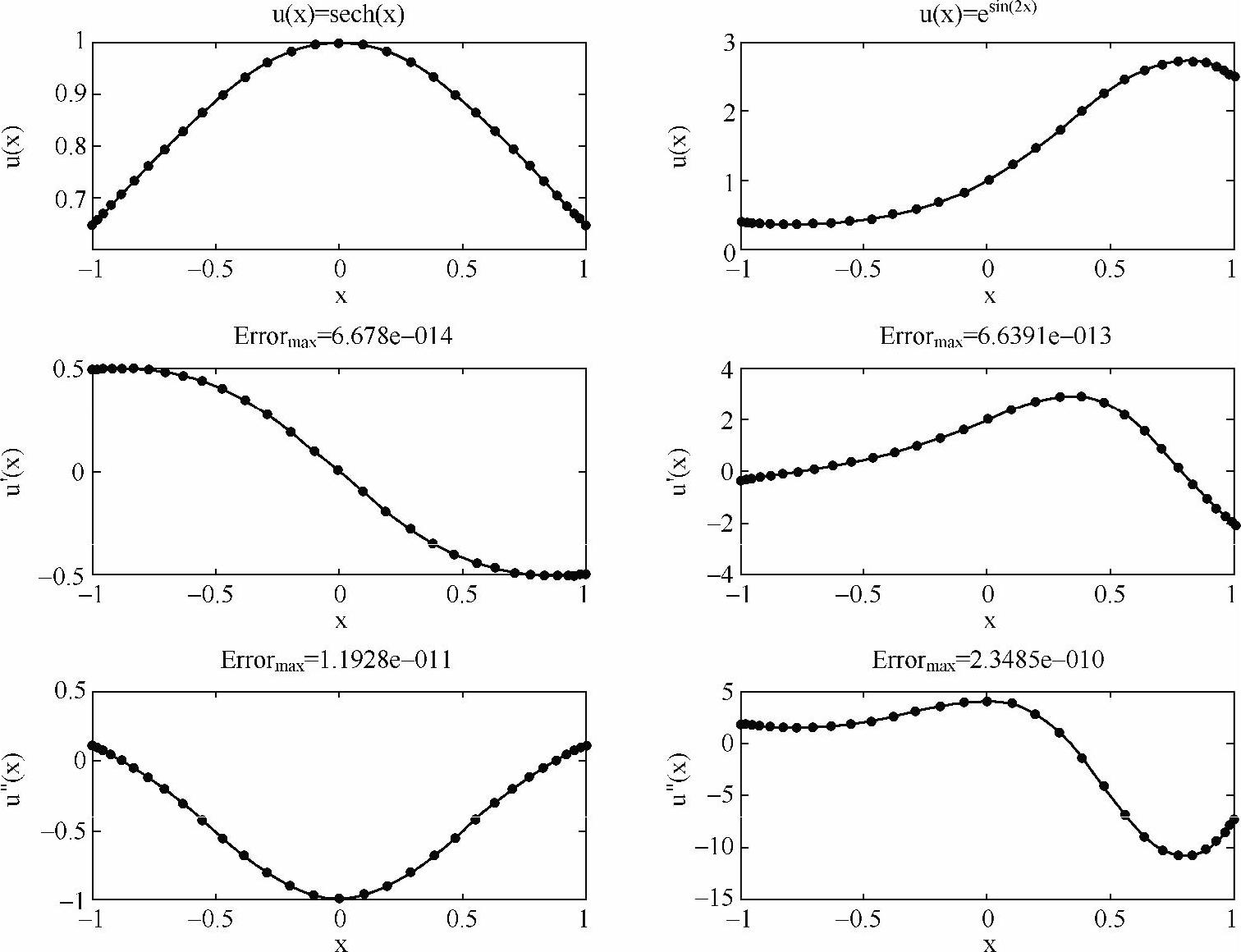
图5-4 用切比雪夫求导矩阵计算u(x)=sech(x)和u(x)=esin(2x)在[-1,1]上的 1、2阶导数的数值解(点)并与精确解(曲线)比较
对于二维问题,先用切比雪夫点分别在x、y方向上划分区间[-1,1],即x=(x0,x1,…,xN)T和y=(y0,y1,…,yN)T。于是在x-y平面的-1≤x,y≤1区域内得到了(N+1)2个点:(x0,y0),(x0,y1),…,(x0,yN),(x1,y0),…,(x1,yN),…,(xN,yN),如图5-5所示,左图中N=8,右图中N=16。
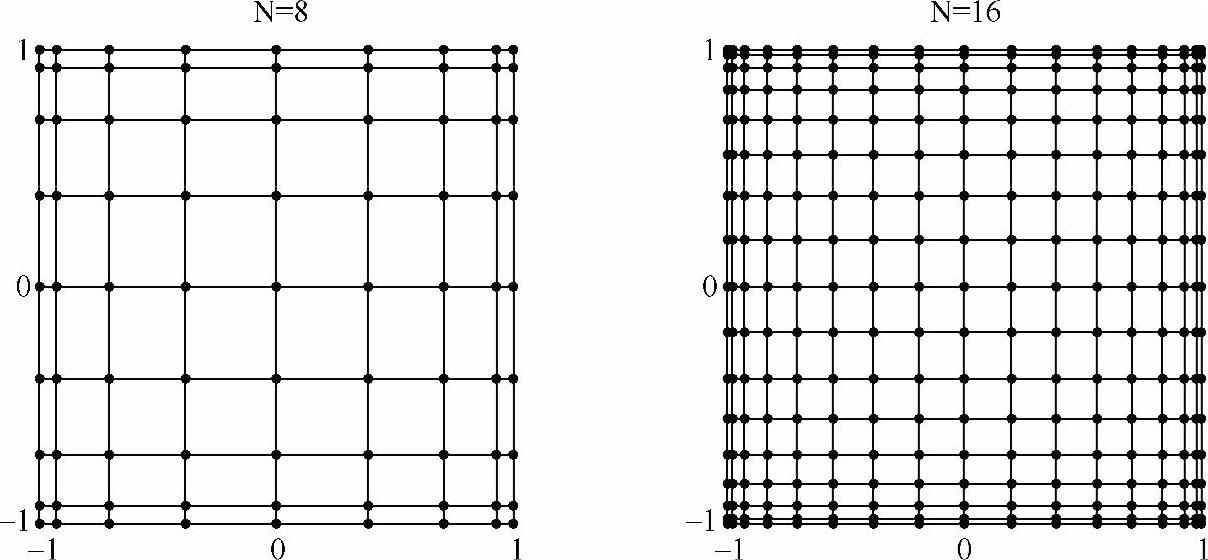
图5-5 用切比雪夫点划分二维区域
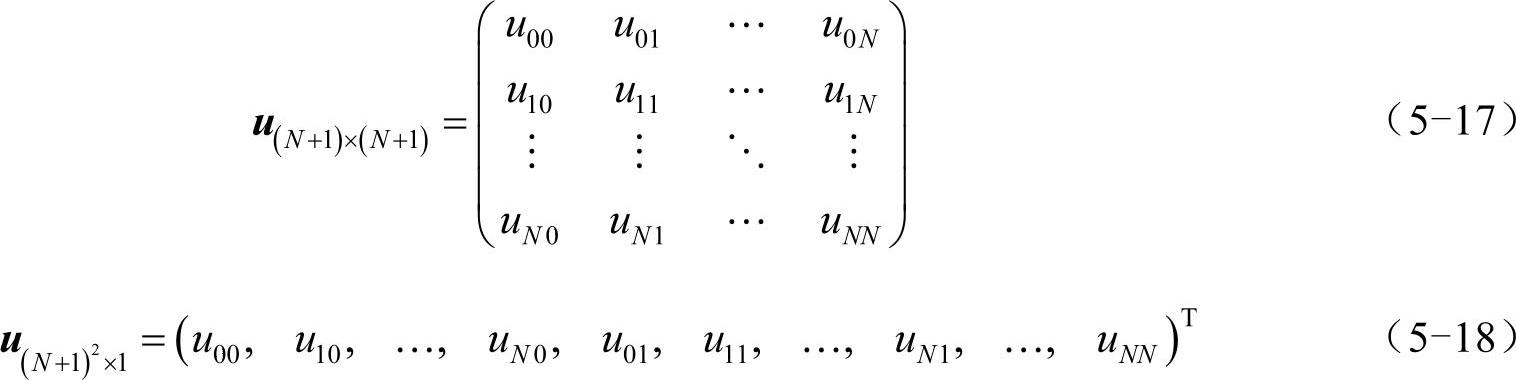
用N+1阶方阵或(N+1)2维向量u表示这些点上的函数值(可用Matlab的reshape函数在二者之间互相转换):
其中,元素uij对应的坐标是(xj,yi)。可将∂nu/∂yn和∂nu/∂xn写为矩阵形式:
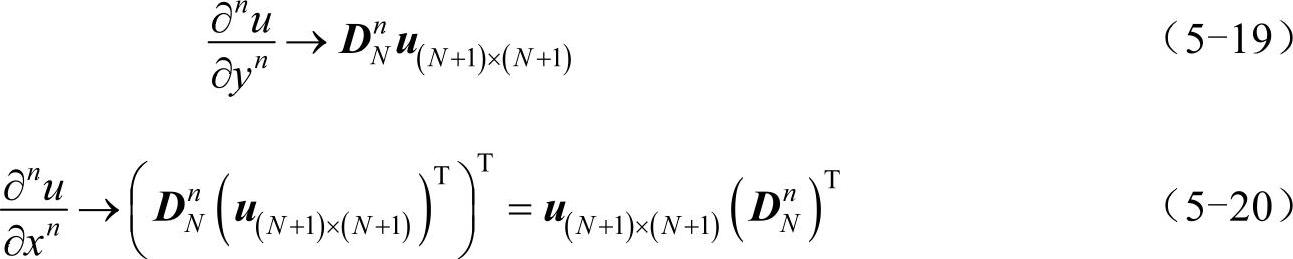
或者写为:
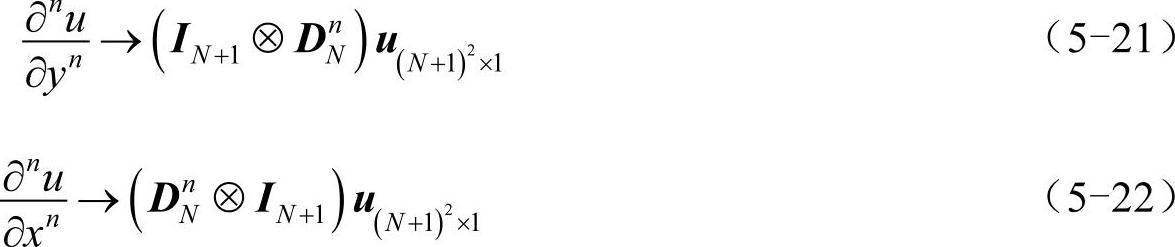
其中,IN+1为N+1阶单位矩阵。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




