Matlab谱方法：高效解法与实现

Matlab的ode系列函数（统称odesolver）专门用于求解形如式（1-53）的常微分方程的初值问题，或者求解形如式（1-54）的常微分方程组的初值问题。ode是常微分方程（ordinary differential equation）的英文缩写。

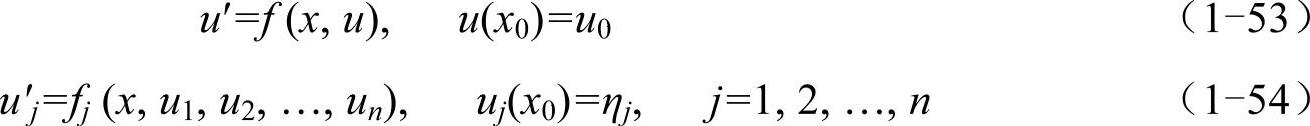
数值求解常微分方程（组）的初值问题一般需要两个文件：主程序文件（如main.m）和定义函数odefun的文件（即odefun.m）。简单来讲，主程序文件main.m包括变量的定义、初始化、odesolver的调用、计算结果的处理和显示。而文件odefun.m中定义的函数odefun用来给出u′(x)（或u_j′(x)）在任一位置的取值，也就是实现f(x,u)（或f_j(x,u₁,u₂,…,u_n)）。后面章节的代码示例可帮助读者更好地理解这两个文件的作用和关系。

ode系列函数的一般调用语法为：

[X,U]=odesolver(odefun,xspan,u0,options,parameter1,parameter2,…)

下面对每一项进行说明：

（1）“odesolver”是所使用的ode系列函数名称，可以是ode45、ode23、ode113、ode15s、ode23s、ode23t和ode23tb中的一个。

（2）“odefun”是定义了f(x,u)（或f_j(x,u₁,u₂,…,u_n)）的函数的句柄，可以是单引号括起来的函数名，也可以是前面加“@”的函数名。

（3）“xspan”为常微分方程（组）自变量x的取值范围。它可以是一个二维向量，如“[x0 xn]”。这种情况下，常微分方程（组）将在该区间上被求解，计算后所返回结果是u(x)（或u_j(x)）在这一区间内某些位置的取值，具体位置由odesolver自行决定。xspan也可以是一个n+1维向量，如“[x0,x1,…,xn]”，这样计算后将返回u(x)（或u_j(x)）在向量xspan中每个元素所对应位置处的数值结果，注意向量xspan中的元素必须按照从大到小或者从小到大的顺序排列。显然，xspan的第一个元素必然是初始条件的位置x₀。

（4）“u0”是一个数值（向量），代表常微分方程（组）初值问题的初始条件，即u(x)（或u_j(x)）在初始位置的取值。当然，初始条件个数等于常微分方程组的方程个数才能求解。

（5）“options”为可选项，它是一个能改变odesolver默认参数设置的结构体，由odeset函数生成。若不改变默认参数设置，可将其设为空，即“[]”。

（6）“parameter1,parameter2,…”为传递给odefun的参数，个数随意决定，是可选项。

（7）计算结果保存到“[X,U]”中，向量X包含一系列位置x₀,x₁,…,x_n，向量（矩阵）U包含u(x)（或u_j(x)）在这些位置的数值解。

使用ode系列函数时还需要定义odefun函数，一般这是一个单独的文件，文件名与函数名相同，即：odefun.m。与odesolver的调用形式相对应，该文件开头声明如下：

function du=odefun(x,u,dummy,parameter1,parameter2,…)

（1）“odefun”为函数名，可随意选取，但是必须与文件名相同。

（2）“x”为自变量。

（3）“u”是常微分方程（组）的u(x)（或u_j(x)）在x处的取值，是一个数值（向量）。

（4）“dummy”是一个用来占位的变量，无实际意义。如果调用odesolver时使用了options，就需要在这里加入一个无用的变量与之对应。dummy在英语中意为傀儡。

（5）“parameter1,parameter2,…”用于接收传递来的参数，注意前面必须有dummy占用一个位置才不会出错。

（6）“du”为函数odefun输出结果的变量名，可随意选取。

这里需要特别强调一下，如果调用odesolver时需要给函数odefun传递参数parameter1,parameter2,…，根据语法，这些参数是排在options后的，所以在options的位置必须有一变量，如无需改变odesolver的默认设置，options的位置只填入“[]”即可。相应地，函数odefun接收参数时也需要在该位置填入一无意义变量dummy。换句话说，由于options排在参数parameter1,parameter2,…之前，所以只要用到传参功能，即使不想通过options改变默认设置，也要占用该位置才不致出错。

若既不传递参数也不改变设置，那么调用odesolver和定义函数odefun的语句为：

[X,U]=odesolver(odefun,xspan,u0)

和

function du=odefun(x,u)

1.1.4小节介绍的龙格-库塔法计算公式实际上属于定步长算法，因为它的步长h为定值。步长h的选取对数值计算有很大影响，过大会导致误差较大，过小则会引起运算量增大以及舍入误差大量积累。这一不足的改进方法就是算法根据误差的情况来自动调整每一步的步长，在方程的解变化快的地方采用小步长，变化慢的地方采用大步长。较之定步长算法，这种变步长算法能更灵活地寻求运算量和误差之间的平衡。

然而，常用的变步长四、五阶龙格-库塔法只适用于非刚性（nonstiff）方程。对于所谓的刚性（stiff）方程，上述变步长算法为了保证精度，会自动采用非常短的步长计算。这就导致计算速度极慢以致无法接受，所以刚性方程由另外的变步长算法来进行数值计算。也就是说，刚性方程和非刚性方程对步长选取的要求存在差异，只能用不同的变步长算法来求解。

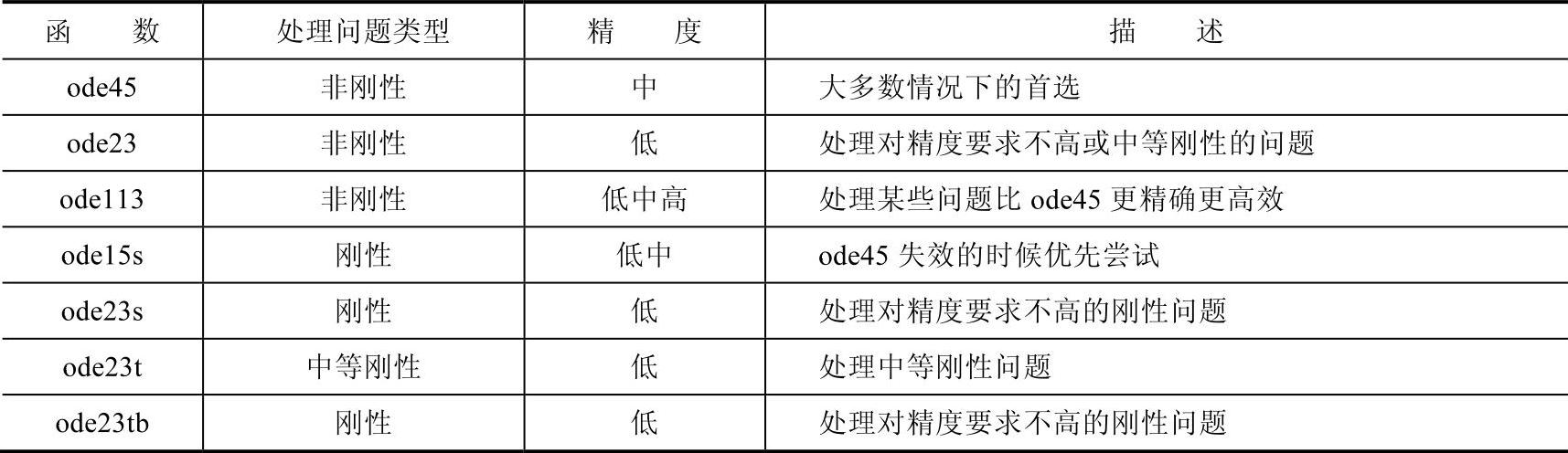
顾名思义，ode45使用的是变步长的四、五阶龙格-库塔法，它的精度适中，可用于求解大多数常微分方程（组），是odesolver中的首选。ode23采用变步长的二、三阶龙格-库塔算法，它的精度略差，但比ode45的计算速度更快。ode23和ode45都属于单步算法，而ode113用了Adams-Bashforth-Moulton多步算法，它的精度和速度在某些情况下会比ode45更高。前面提到的这三种odesolver都仅适用于非刚性方程（组）。针对刚性方程（组）只能用ode15s、ode23s、ode23t、ode23tb。如果不能判断常微分方程（组）是否刚性，优先推荐选用ode45求解，遇到运行失败或者迟迟不见输出结果的情况，再用ode15s，这样可以处理绝大多数的常微分方程（组）。仍不行的话就尝试其他的odesolver。表1-2给出了ode系列函数的基本介绍。

表1-2 ode系列函数简介

(www.xing528.com)

下面以初值问题（1-55）为例，示范几种数值方法的代码实现。

上式的解析解为：u=2e-3x+2x+1。这里分别用欧拉法、预测-校正法、ode45求解该问题，并分别计算三种方法的数值解与解析解的误差。代码如下：

程序1-1

在调用ode45时，因为表达式u′=-3u+6x+5比较简单，所以没有单独新建一个函数文件，而是使用了匿名函数（anonymous function）。定义匿名函数的语法为：

fhandle=@(arglist)expr

“fhandle”为函数句柄。“arglist”为该函数的参数列表，多个参数以逗号隔开。“expr”为该函数的表达式。代码中的“@(x,u)[-3^*u+6^*x+5]”与新建一个odefun.m文件，里面填上如下内容是等效的。

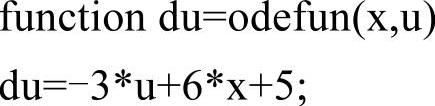
使用匿名函数可以减少一个函数文件，但仅针对函数表达式很简单的情况。由于本书后面所解决的问题都比较复杂，所以其余代码都将使用创建函数文件的方法。运行代码得到结果如图1-2所示。可以看到，在步长同为h=0.05的情况下，欧拉法的数值结果明显偏离了解析解，而预测-校正法、ode45的数值结果与解析解重合得较好。

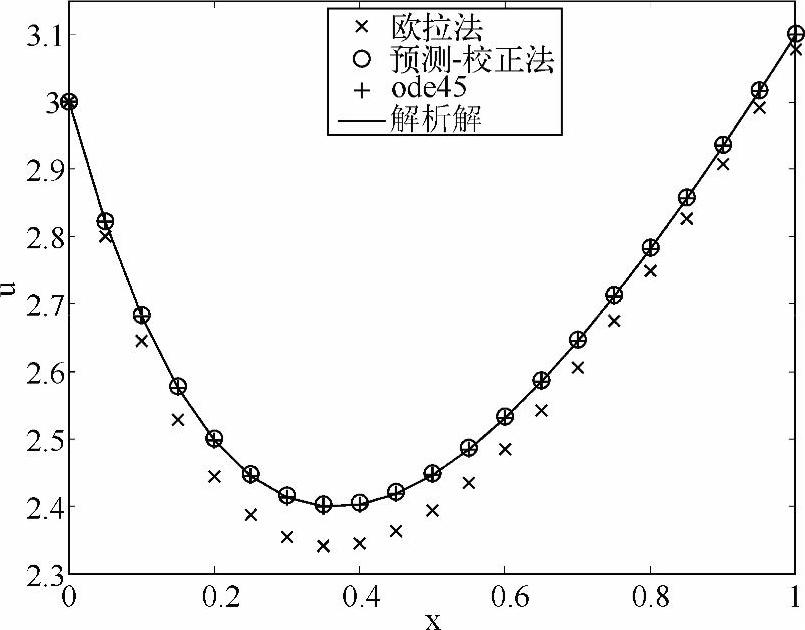
图1-2 用欧拉法、预测-校正法、ode45求出数值解，并与解析解相比较

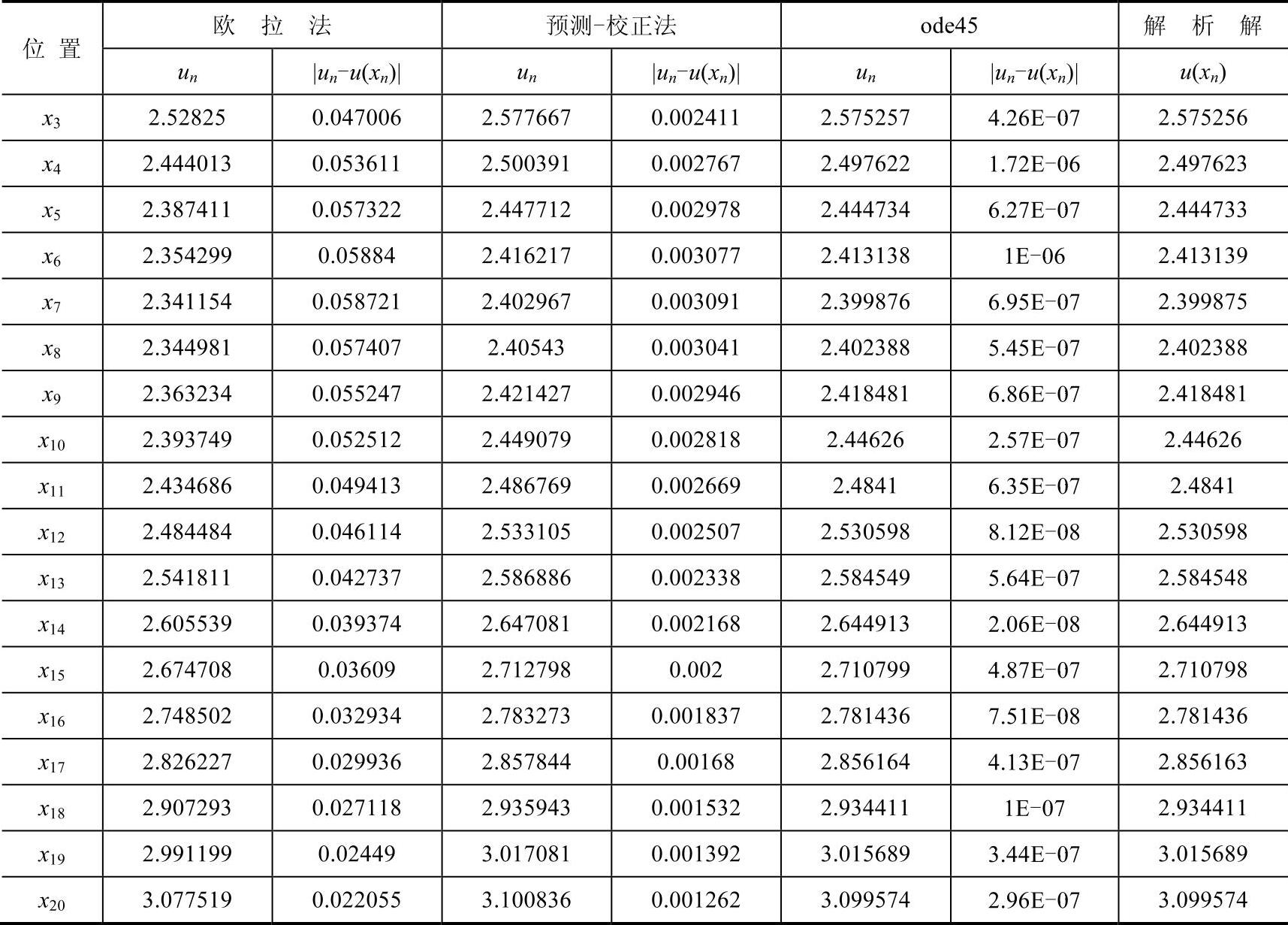
表1-3列出了三种方法在每个位置所得数值结果以及误差。显然，三者在误差上的关系有：欧拉法>预测-校正法>ode45，这与此前局部截断误差的分析结果是一致的。

表1-3 欧拉法、预测-校正法、ode45的数值结果与解析解的比较

（续）

接下来再给出一个数值求解刚性方程组的例子。van der Pol方程是Matlab帮助文件提到的一个很典型的刚性问题，表达式可写成如下形式：

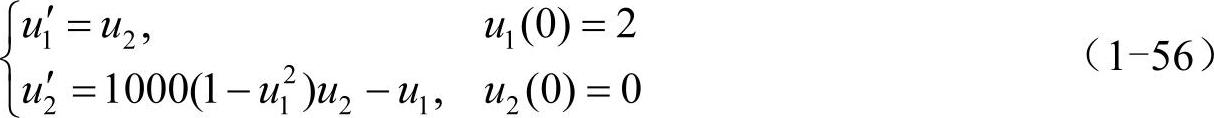
用专门处理刚性方程的ode15s在区间[0,3000]上数值求解u₁(x)，代码如下：

程序1-2

主程序代码如下：

文件vdp.m代码如下：

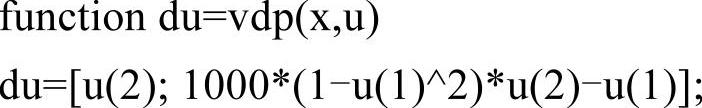
vdp.m文件中定义的vdp函数将u₁′、u₂′的值放在一个二维向量中输出。此外，存放计算结果的变量U是一个两列的矩阵，分别对应于u₁和u₂的数值结果。这是求解具有两个方程的方程组与求解一个单独方程的差别。程序输出如图1-3所示，可以看到u₁在某些位置的变化十分剧烈。如果将代码中的ode15s换成针对非刚性问题的ode45，CPU占用率将长时间维持在100%，并且迟迟得不到计算结果；而这对于ode15s只需要一瞬间，这说明处理刚性/非刚性方程时采用正确的方法可以事半功倍。

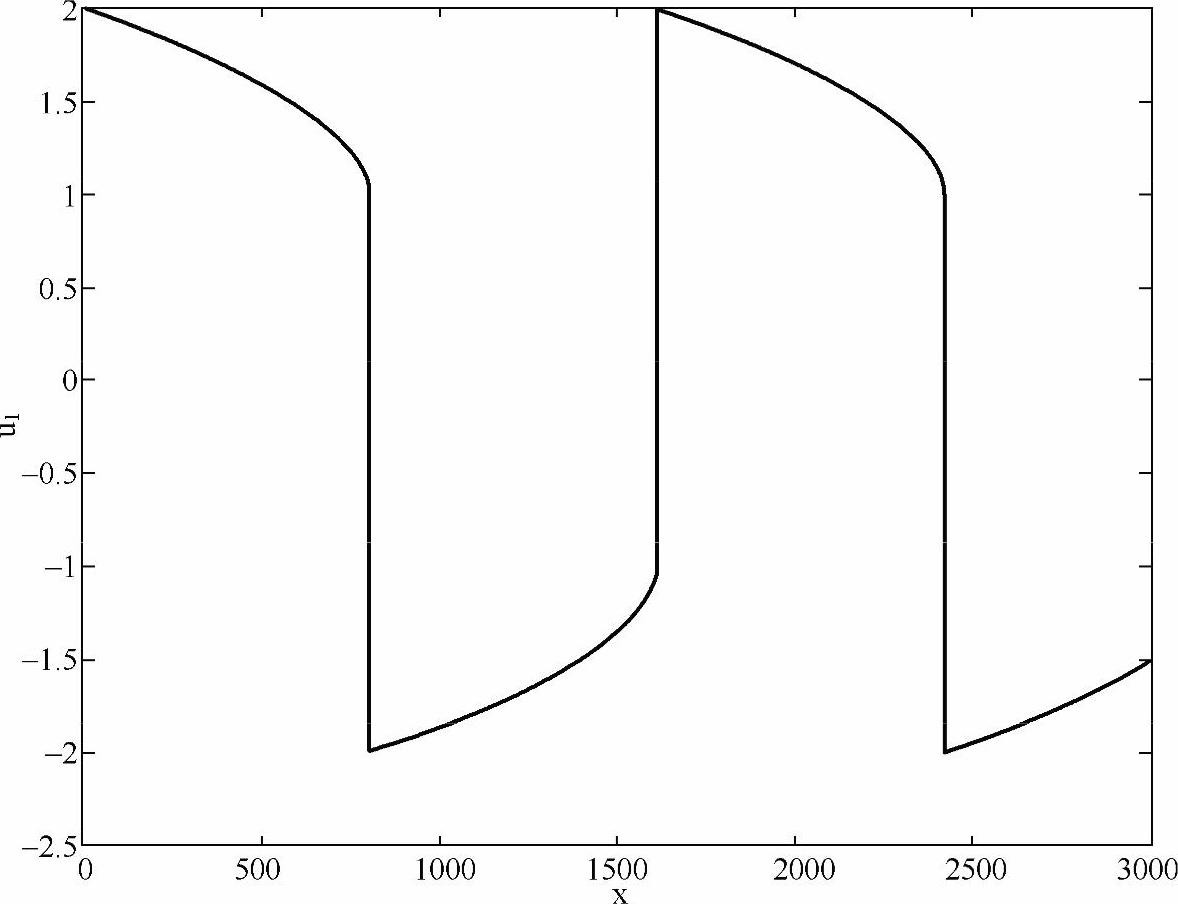
图1-3 刚性问题van der Pol方程的数值解