数理方程应用实例：分离变量法

分离变量法作为求解数学物理方程的基本方法之一，其基本思想是将多变量的偏微分方程转化为几个单变量的偏微分方程，以便逐一求解。18世纪初，傅里叶首先利用这一方法求解偏微分方程，也正是这种求解过程展示了傅里叶级数的作用与威力，故分离变量法也称为傅里叶方法。定解问题（1.20）描述的是一维细杆热传导过程，杆的一端为第一类边界条件，温度恒定，另一端为第三类边界条件，为对流换热边界条件，求此细杆内的温度分布。在热传导问题中，不同点的传热规律相同，不同的仅是温度，因此温度分布可以表示为

式中，X（x），T（t）分别表示仅与x有关和仅与t有关的函数。把式（1.21）代入定解问题（1.20）的方程，得到

等式只有在两边均等于常数时才成立。取常数为－λ，则有

这样，方程（1.22）就被分离为两个常微分方程，其中一个仅含有自变量t，另一个仅含有自变量x，我们可以通过求解这两个方程来决定T（t）及X（x），从而得到方程的特解。

根据边界条件，X（x）应当满足

（1）当λ＜0时，通解为

根据方程组（1.25），可得

只能C1＝C2＝0，所以λ＜0没有非平凡解。

（2）当λ＝0时，通解为

根据方程组（1.25），可得

因而C1＝C2＝0，所以λ＝0没有非平凡解。

（3）当λ＞0时，通解为

根据方程组（1.25），可得

为使X（x）为非平凡解，λ应满足

即λ应是下述超越方程的正解：

令

则变为

利用图解法或数值求解法可得出方程（1.33）的根。如图1.1所示，方程（1.33）由图解法可知，有可列无穷多个正根vk＞0（k＝1，2，…），满足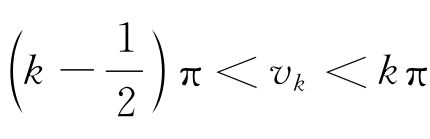。因此特征值问题存在无穷多个固有值

及相应的固有函数

把λ＝λk代入方程（1.23），可得

于是得到可分离变量的特解

由于方程及边界条件都是线性的，故可利用叠加原理构造级数形式的解：

图1.1　超越方程的解

根据初始条件，可得

为确定系数Ak，须先证明固有函数系在［0，l］上正交。设固有函数Xn和Xm分别对应于不同的固有值λn和λm，即

以Xm和Xn分别乘上面第一和第二式，两式相减后在［0，l］上积分，利用Xn和Xm都满足定解问题（1.20）中的边界条件，得到

由于λn≠λm，故得固有函数系的正交性：(www.xing528.com)

记

于是，在式（1.39）两边乘以，再进行积分，利用正交性即可得

将式（1.43）代入式（1.38），就得到初边值问题的形式解为

例1.3　一长度为l的均匀细棒，其周围以及两端x＝0、x＝l均为绝热，初始温度分布为u（x，0）＝f（x），求杆内的温度分布，并证明当f（x）等于常数u0时，恒有u（x，t）＝u0。

解　u（x，t）满足方程

由分离变量法

u（x，t）＝X（x）T（t）

则

（1）当λ＜0，通解为

则

由于

只能

C1＝C2＝0

所以，λ＜0没有非平凡解。

（2）当λ＝0，通解为

X（x）＝C1x＋C2

则C1＝0，C2为任意常数。所以

X（x）＝C2

则

u（x，t）＝C0

（3）当λ＞0，通解为

则

由初始条件

则

当f（x）＝u0时，