数理方程：格林函数概念及应用案例

由调和函数的基本积分公式（3.18）可知，一个调和函数u在区域Ω内的数值依赖于它本身及其外法线方向导数在边界Γ上的值。对于拉普拉斯方程的狄利克雷边值问题，u｜Γ已知，未知；对于拉普拉斯方程的诺伊曼边值问题，已知，u｜Γ未知。根据解的唯一性，拉普拉斯方程的任意边值问题都不能同时给出u｜Γ和的信息，因此若要利用公式（3.18）求解拉普拉斯方程的狄利克雷边值问题，需要消去积分表达式中的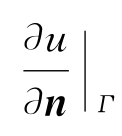，这就需要引进格林函数的概念。

假设函数u，v都是区域Ω内的调和函数，由格林第二公式可得

将此式与式（3.18）相加，可得

若调和函数v满足

则式（3.27）中含有的项就可以消去。

令

则式（3.27）可表示为

G（M，M0）即为拉普拉斯方程狄利克雷边值问题在区域Ω上的格林函数（或者称为狄利克雷问题的源函数）。由式（3.28）知G（M，M0）在边界Γ上恒等于零，因此，如果格林函数G（M，M0）已经知道，并且它到边界为止具有一阶连续偏导数，则对于拉普拉斯方程狄利克雷边值问题(www.xing528.com)

解可表示为

对于泊松方程狄利克雷边值问题

解可表示为

这种将边值问题的解用格林函数或者其导数的积分来表示的方法称为格林函数法。

采用格林函数法，对任意函数求拉普拉斯方程或泊松方程狄利克雷边值问题就转化为求此区域的格林函数。但要知道区域上的格林函数，却必须求解调和方程的一个特殊的狄利克雷问题：

虽然对于一般区域，求解问题（3.32）也是同样困难的，但格林函数法还是有意义的，这是因为：①格林函数仅依赖于区域，而与边界条件无关。一旦求得了某个区域上的格林函数，这个区域上一切狄利克雷问题的解的存在性也就得到了解决，且其解可用积分式表达出来。②对于某些特殊的区域如球、半空间等，格林函数可以用初等方法求得，而这些特殊区域上的狄利克雷问题常常起着重要的作用。