调和函数的基本性质及应用案例

利用格林公式可以推导出调和函数的积分表达式及一些基本性质。

1）调和函数的积分表达式

调和函数的积分表达式就是调用调和函数及取在区域边界Γ上的法向导数沿Γ的积分来表达调和函数在Ω内任意一点的值。设M0（x0，y0，z0）是区域Ω内的某一固定点，构造函数

函数除点M0外处处满足调和方程（3.2），称为三维调和方程的基本解。由于函数v在区域Ω内有奇异点M0，因此对区域Ω不能直接应用格林第二公式。为此，在区域Ω内建立一个以M0为中心、充分小正数ε为半径的球Kε，在Ω内挖去球Kε，则在剩下的区域Ω\Kε中函数v就是连续可导的了。在区域Ω\Kε上对上述函数u和v应用格林第二公式，可得

式中，Γε是球Kε的表面。在区域Ω\Kε内，Δu＝0，。在球面Γε上，由于

因此

式中，u*为函数u在球面Γε上的平均值。类似地，有

式中，为函数在球面Γε上的平均值。将上面两式代入式（3.16），得

令ε→0，由于u（x，y，z）是连续函数，所以；由于u（x，y，z）一阶连续可微，故有界，所以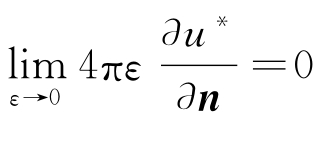。则式（3.17）转化为

式（3.18）即为调和函数的基本积分公式。

由式（3.18）可知，对于在Ω∪Γ上有连续一阶偏导数的调和函数u，其在区域Ω内任一点M0的值，可通过积分表达式（3.18）用这函数及其法向导数在区域边界Γ上的数值来表示。

上述推导是在假设点M0（x0，y0，z0）为区域Ω中的点而进行的。如果把M0点取在Ω之外或者取在Ω的边界Γ上，可以类似地得到另外两个式子。把它们与式（3.18）合并起来可写为

如果u在Ω∪Γ上有连续的一阶偏导数，而在区域Ω内，Δu＝F，则调和函数的基本积分公式为

对于二维情形，拉普拉斯方程的基本解为

相应地关于调和函数的基本积分公式为

式中，u（M）为平面区域Ω上的调和函数，在Ω∪Γ上有连续一阶偏导数，Γ为Ω的边界。

2）诺依曼内问题有解的必要条件

设函数u在以曲面Γ为边界的区域Ω内的调和函数，在Ω∪Γ上有连续一阶偏导数，则格林第二公式（3.14）中取u是所给的调和函数，取v≡1，则

由此可得诺依曼内问题（3.6）有解的必要条件为

事实上，此条件也是诺依曼内问题有解的充分条件。

3）调和函数的平均值公式

设函数u（M）在某区域Ω内调和，M0是Ω中的任一点，Γa表示以M0为中心、a为半径并且完全落在区域Ω内部的球面，根据式（3.20），且在Γa上，

则(www.xing528.com)

即

式（3.25）即为调和函数的球面平均值公式，表示调和函数在定义域Ω内某一点的值，等于它在该点为球心且包含于Ω的球面的平均值。

4）调和函数的极值原理

定理：假设函数u（x，y，z）在区域Ω内调和，如果u（x，y，z）不是常数，则u（x，y，z）在Ω内既达不到最大值，也达不到最小值。

证明　用反证法证明。设调和函数u（x，y，z）不恒等于常数，且在区域Ω上的上界为m（这里自然假设函数u（x，y，z）在区域Ω上有上界，在相反的情形下，定理是显然成立的），而u（x，y，z）在Ω内某点M0取值m，我们来引出矛盾。

以M0为球心、任意半径R作球K，使它完全落在区域Ω中。记K的球面为SR，在SR上必成立u≡m。事实上，如果u在球面SR上某一点其值小于m，则由函数的连续性，必可找到此点在球面SR上的一个邻域，在此邻域中u＜m。因此u在SR上的积分平均值

但由平均值公式，有

这就发生了矛盾。因此在球面SR上，u恒等于m。同理，在以M0为心、任意r（r≤R）为半径的球面上，u也恒等于常数m，因此，在整个球K上u恒等于常数m。

现在证明对Ω中的所有点u都恒等于常数m。任取一点M1∈Ω，在区域Ω中作联结M0及M1两点的折线γ，再用完全落在Ω中的有限个球K1，K1，…，Kn盖住γ，使得K1的球心为M0，K2的球心落在K1中，K3的球心落在K2中，…，Kn的球心落在Kn－1中（图3.1）。

根据上述证明方法，可以依次证明在所有这些球所包围的区域上u≡m，因此，特别有u（M1）＝m。由M1的任意性，就得到在整个区域上u（x，y，z）≡m，这和u不恒等于常数相矛盾。因此u不能在Ω内部取到其上界。因为－u也是调和函数，从它在Ω的内部不能取到它的上界，就得出u也不能在Ω内部取到其下界。这就证明了极值原理。

图3.1　调和函数极值原理证明示意图

推论1　在有限区域Ω内调和、在Ω∪Γ上为连续的函数必在边界Γ上取得其最大值和最小值。

推论2　设u及v都是区域Ω内的调和函数，且在Ω∪Γ连续。如果在Ω的边界Γ上成立着不等式u≤v，那么在Ω内上述不等式也成立；并且只有在u≡v时，在Ω内才会有等号成立的可能。

5）拉普拉斯方程解的唯一性问题

假使有两个调和函数u1（x，y，z）和u2（x，y，z），它们在有界区域Ω的边界Γ上完全相同，则它们的差u＝u1－u2在Ω中也满足调和方程，而在Γ上等于零。根据极值定理，函数u在区域Ω上最大值及最小值均为零，即u≡0。因此，u1≡u2，即狄利克雷内问题的解存在，必是唯一的。

设在区域Ω的边界Γ上给定了函数g和g*，而且在Γ上处处成立｜g－g*｜≤ε，这里ε是一个给定的正数。设u，u*分别是调和方程（3.1）在区域Ω上以g和g*为边界条件的狄利克雷内问题的解，那么调和函数u－u*在Γ上取值g－g*，则

因此，在Ω上各点有

｜u－u*｜≤｜g－g*｜≤ε

即狄利克雷内问题的解连续地依赖于所给的边界条件。

总的来说，狄利克雷内问题的解存在，必是唯一的，而且连续地依赖于所给的边界条件g。

同样可证，对于调和方程（3.2）的狄利克雷外问题的解如果存在，则必是唯一的。