区间估计的定义-《概率论与数理统计》

对于一个未知参数，人们只知道它的点估计有时还不能满意，还希望给出未知参数的一个范围，并希望知道这个范围包含参数真值的可信程度．为此，引进区间估计的有关概念．

定义7．3．1　设总体X的分布函数F（x；θ）含有一个未知参数θ，对于给定值α（0＜α＜1），若由样本X 1，X 2，…，X n确定的两个统计量和，对于θ∈Θ满足

则称为θ的置信水平为1-α的置信区间和分别称为置信水平为1-α的双侧置信区间的置信下限和置信上限，1-α称为置信水平．

式（7．3．1）的含义如下：若反复抽样多次（各次得到的样本的容量都相等），每个样本观察值确定一个区间，每个这样的区间要么包含θ的真值，要么不包含θ的真值，按伯努利大数定律，在这么多区间中，包含θ真值的约占100（1-α）／100，不包含θ真值的约占100α／100．例如，若α＝0．05，反复抽样100次，得到100个区间中，其中不包含θ真值的约5个．在例7．3．1后面，将结合具体问题给出解释．

例7．3．1　设X～N（μ，σ2），σ2为已知，X 1，X 2，…，Xn是来自X的样本，求μ的置信水平为1-α的置信区间．

解　由于为μ的无偏估计量，且有

按标准正态分布的上侧α分位点的定义，有

按定义7．3．1，我们就得到了μ的置信水平为1-α的置信区间

如果取α＝0．05，即1-α＝0．95，查表得．若σ＝1，n＝16，于是得到一个μ的置信水平为0．95的置信区间

如果＝5．20，代入得一个区间（4．71，5．69）．

若μ＝5．25，σ＝1，可以用随机模拟法产生100组N（5．25，1）的随机样本，每组样本包含50个观察值，现在画出100个μ＝5．25的置信水平为1-α＝0．95的置信区间，如图7-3所示．

同样，若μ＝5．25，σ＝1，可以用随机模拟法产生100组N（5．25，1）的随机样本，每组样本包含50个观察值，现在画出100个μ＝5．25的置信水平为1-α＝0．90的置信区间，如图7-4所示．

图7-3　100个置信水平为0．95的置信区间(www.xing528.com)

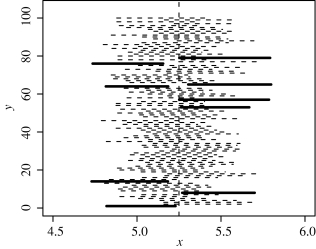
图7-4　100个置信水平为0．90的置信区间

从图7-3可以看出，100个区间中有94个包含参数真值5．25，另有6个区间不包含参数真值．这就是置信水平为1-α＝0．95的置信区间的一个解释．

从图7-4可以看出，100个区间中有91个包含参数真值5．25，另有9个区间不包含参数真值．这就是置信水平为1-α＝0．90的置信区间的一个解释．

然而，置信水平为1-α的置信区间并不是唯一的．如对以上的例7．3．1，若给定α＝0．05，则

这样，我们又得到了μ的另一个置信水平为1-α的置信区间

在式（7．3．3）中，令α＝0．05，再比较由式（7．3．4）给出的μ的置信水平为0．95的置信区间的长度．

由式（7．3．3）给出的置信区间的长度为

由式（7．3．4）给出的置信区间的长度

显然，，即由式（7．3．3）给出的区间比由式（7．3．4）给出的区间短．当然，对于同一个置信水平，区间的长度越短越好．

通过以上的例子，可以看到寻找未知参数θ的置信区间的具体做法如下：

（1）寻找一个样本X 1，X 2，…，Xn的函数W＝W（X 1，X 2，…，Xn；θ），它包含待估参数θ，而不包含其他未知参数，并且W的分布已知且不依赖任何未知参数（当然不依赖于待估参数θ）．

（2）对于给定的置信水平1-α，定出两个常数a，b，使

（3）若能从a＜W（X 1，X 2，…，X n；θ）＜b得到等价的不等，其中都是统计量，那就是θ的置信水平为1-α的置信区间．

函数W（X 1，X 2，…，Xn；θ）的构造，通常从θ的点估计着手．常用的正态总体参数的置信区间可以用上述步骤推得．