实用微积分：一、二元函数的极值解析

定义 设函数z=f（x，y）在点（x0，y0）的某个邻域内有定义，如果对于该邻域内异于（x0，y0）的点（x，y）都有

则称f（x0，y0）为函数f（x，y）的极大值或极小值.极大值与极小值统称为极值，使函数取得极值的点（x0，y0）称为极值点.

例如，函数f（x，y） =x2+y2在点（0，0）处的函数值f（0，0） =0，而当（x，y） ≠（0，0）时，f（x，y） =x2+y2＞0，所以在点（0，0）处函数取得极小值0，又如，可以看出，f（x，y） =1-x2-y2在点（0，0）处取得极大值1.

在一般情况下，函数的极值并不容易看出，因此与一元函数一样，需要研究二元函数极值存在的必要条件和充分条件.

定理1 （极值存在的必要条件） 设函数z=f（x，y）在点P0（x0，y0）处有极值，且在点P0（x0，y0）处的偏导数存在，则函数z=f（x，y）在点P0（x0，y0）处的两个偏导数必为零，即

如何判断驻点是不是极值点呢？在一元函数极值中，有一种方法是用函数在驻点处的二阶导数的符号去判断的.对于二元函数，也有类似的方法.

定理2 （极值存在的充分条件） 设P0（x0，y0）为函数z=f（x，y）的驻点，且在点P0（x0，y0）的某邻域内，z=f（x，y）具有二阶连续偏导数.记A=f″xx（x0，y0），B=f″xy（x0，y0），C=f″yy（x0，y0），Δ=B2-AC，则：

（1）当Δ＜0 时，函数z=f（x，y）在点P0（x0，y0） 处有极值，且当A＜0 时，有极大值，当A＞0 时，有极小值；

（2）当Δ＞0 时，函数z=f（x，y）在点P0（x0，y0）处没有极值；

（3）当Δ=0 时，函数z=f（x，y） 在点P0（x0，y0） 处可能有极值，也可能没有极值.

根据定理1 和定理2，若函数z=f（x，y）的二阶偏导数连续，则可按下列步骤求函数的极值：

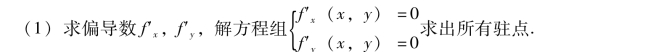(www.xing528.com)

（2）对于每一个驻点（x0，y0），求出二阶偏导数的值A，B，C.

（3）确定Δ=B2-AC的符号，按定理2 的结论判定f（x0，y0）是否是极值，是极大值还是极小值.对于有多个驻点的情形，步骤（3）可列表进行.

【例1】 求函数f（x，y） =x3+y3-3xy的极值.

解 （1）求偏导数，得f′x（x，y） =3x2-3y，f′y（x，y） =3y2-3x

解方程组

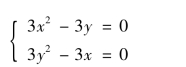
得驻点P1（0，0）和P2（1，1）；

（2）求二阶偏导数，得f″xx=6x，f″xy=-3，f″yy=6y；

（3）列表判定（表6-2）.

表6-2

因此，f（x，y）有极小值f（1，1） =-1.