普通聚落的发展规律：比例发展模型

在上一章中，我们假设城市在狩猎采集社会出现是由于人类归属于一个聚落以繁衍后代和自我防御的需要，同时也是为了实现社会交流和劳动分工以改善物质条件，也就是为了发挥集聚经济效应。关于生命起源本身，传统的观点大致认为，生命起初是由于一次偶然的电击引发了同质的“原始汤”中的化学反应，从而催生了多种多样的核苷酸，这些核苷酸继而构成了生命的基石——RNA（核糖核酸）和DNA（脱氧核糖核酸）。同理，我们可以推测，社会和城市起初是一些随机分布的家庭单元，各自之间的活动间距取决于狩猎和采集所能获得的食物量。这些单元，当然，出于生存的需要会有往来，但是这个时期主要的模式还是家庭单元之间互相争夺领地，因为领地大小关乎生存。渐渐地人们就意识到，相较于竞争，合作能带来更大的生存希望，所以人们建立了村庄和乡落，最初的目的在于保障自身的防御力量，随着时间的推移，由此带来的社会交往慢慢地推动了劳动分工，并带来了财富的增长。

我们将从上一章中提及的模型讲起，在这个模型中，人口单元——家庭、聚落或者群体，随机发展但是基本与它们自身的规模成比例。类似于“原始汤”，在最初毫无差别的聚落中，一些单元比另一些获得了更快的发展，这仅仅是因为它们总是能抢占先机，而其他的单元则落后于潮流，最终往往不幸消失。就这样，那些我们称之为城市的大规模聚落出现在了地图上，而正是这些聚落构成了城镇网。等级是这一结构中不可或缺的一部分，但是在我们说明等级如何在这一发展过程中出现之前，我们先退一步来说明在这个人类创造的世界里城市如何根据规模组织起来。在这里我们把等级定义为基于规模的自然排序，其中规模可以通过多种不同的方式来测算。在城镇中，规模大小往往取决于人口、家庭或者劳动力的数量，但也有可能取决于占地面积，能源消耗或者是区域影响力。让我们先看看最简单的一种可能性：同样规模的聚落在一个平面上随机分布。在这样的世界里，聚落的存在是个随机事件。这个模型与上一章所介绍模型的一大区别就在于这一模型中的城市和聚落都是基于空间意义上的网格的。我们将会看到，这对于理解等级结构如何演化出城市系统或中心地是十分关键的。

我们假设在这一过程中，一个地区是随机发展的，但是其发展速度与自身规模是成比例的。那么，假如一个地区i在t时规模为Pi（t），发展速度λi（t+1）是随机的，则该地发展或衰退后的规模可以表示为：

方程5.1与方程4.3是相同的，所以如果用迭代法解方程5.1，就可以测算出不同时间段所对应的发展速度。这些数据反映了任一地区或者网格i在随机发展过程中成比例扩大的趋势。这个结论初看时会觉得出乎意料，但是深思之后，就会觉得合乎情理。

在一个包含许多地区的地域体系中，在任一时间t，所有地点，从小到大，发展速度都是一致的，有可能都是负值，也有可能都是正值。然而，随着时间的推移，一个不断扩张的地区获得持续高速发展的机会就会越来越小。同样，如果一个地区规模不断减小，其衰退的速度也会随时间推移而放缓，当然在这一情况下，如果一个地区变得太小了，那么可以说它就是消失了。所以这一发展或衰退的过程存在着一种内在的不对称性。事实上，越来越少的地方会变得极其之小，而我们往往也会降低判定一个地方消失的标准。如果我们把这个发展过程应用于少数几个对象上，然后从一个给定的区间内选择随机发展速度，反复代入方程5.1，我们就能够很轻易地得出结果。规模变大的对象数量会越来越小，大多数保持在规模较小的水平，而有一部分则直接消失了，但是问题的关键在于：这样的规模分布中有没有什么规律？在上一章中，我们把这一现象解释为人口规模的比例定律，即规模大的对象数量会远远小于规模小的对象，现在，基于我们的网格，我们来看个例子，虽然不是实例，但是却形象地说明了这一点。(www.xing528.com)

我们的例子基于一个21×21的网格，最初设定的人群均匀地分布在网格里的441个对象，也就是地区里，其中Pi（t）=1，∀i，t=0。发展速度λi（t+1）是从区间-0.1＜λi（t+1）＜0.1中随机选择的任一数值。方程5.1的比例发展模型能迅速地将对象按规模大小分类，当t=100时，频率分布很明显就是对数正态分布。事实上，这个模型我反复运行了1 000次，形象地说就是运行了一千年。在这1 000年的模拟中，对象之间在相对规模上有很大的变动。当然，这一点在第4章中我们也用实例说明了，所以在这里我们要探究这一变动的意义。与往常一样，我们根据规模大小对频率进行分类，然后将它们按顺序绘制在图上，由此对这些规模分布进行特征提取。这种位序-规模分布（即齐普夫分布）事实上是非累进式的，我们在第4章中已经通过方程4.5到4.9得出了这一结论。在图5.1中，我们绘制了t=1 000时的位序-规模分布。很明显，这是一个对数正态分布，是人口规模对位序的对数变换。

实际上，很多之前的学者都证明了这种随机发展会导致规模呈对数正态分布（Pumain，2000）。吉布列（Gibrat，1931）是第一个提出关于城市和收入分布理论的学者，但是尤尔（Yule，1925）比吉布列更早了解这一模型及其结果。如果我们继续延长时间，取大于1 000的t值，就会发现人口会越来越趋于汇合，并且最终，我们假设，在这样的离散系统里，所有活动都会聚集到一个中心点上。然而，这样的模拟系统，实际上为不可分割性所局限。因而，为了完善原有的模型，我们有必要引入一个规模阈值，一旦低于这个阈值，人口就不会再减少。这样，无论何时人口单元i低于这个阈值，都会被恢复到阈值，这一机制可以起到防范和补足的效果。这也可以看成是，在一个旧城市消失的同时引进了一个新城市，这就构成了一个完美平衡的生灭过程。用数学语言表示为：

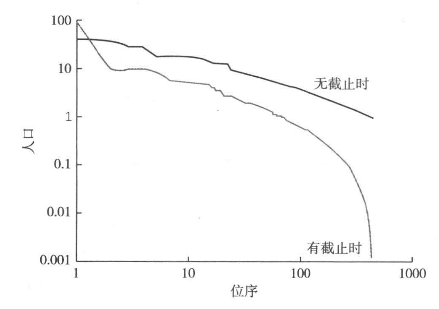
图5.1　通过比例效应和幂律比例缩放并设置最小阈值得出对数正态分布

观察图5.1中的对数正态分布，我们可以看到两个部分，长尾部分几乎呈线性，短尾部分则代表规模较小的聚落点。我们很容易会认为，长尾部分可以用一条直线，或者一种比例关系去逼近，然而事实上，如果我们采用上述机制设定阈值，那么单纯从表面上看，我们就已经有效地截掉了短尾部分。运用相同的速度参数，再次运行方程5.2，当t=1000时，我们就可以得到图5.1中的“近似”线性分布，这与我们上一章中谈到的图4.2b颇为相似。很明显，设置阈值是有作用的，现在我们得出的就不再是呈对数正态分布的曲线了，而是成比例关系的，因为它可以用幂律逼近，其中人口规模Pi（t）与位序ri（t）成反比，表示为，γ=（α-1）-1，就是所谓的比例参数。注意，这一比例关系与方程4.5到4.9推导得出的结论一致，其中α就是概率密度函数参数，与城市规模的频率成比例。当城市在等级结构中上升或下降时，我们很可能把长尾部分看成“稳定状态”。确实，理论家如加贝克斯（Gabaix，1999）曾指出，吉布列过程就是这样的，不断聚合到一点，最后形成一个纯粹的比例法则（齐普夫法则），其中参数α=2，γ=1。注意，我们这里使用长尾和短尾这些术语只是为了更为形象地描述图5.1中的位序-规模分布，在其他语境中，这些术语使用的情况刚好是相反的（Anderson，2006）。