基于不同方法的水资源配置优化模型及解决方案

(一)线性规划

线性规划一般是用来解决约束条件为线性等式或不等式、目标函数为线性函数的最优化问题。这种方法一般多用于解决水资源的分配型问题、存储型问题等。

1.问题的提出

在水资源优化配置过程中,经常会面临两类问题:一是如何在既定任务下寻求完成任务且使系统费用最小或者净效益最大的水资源最优分配方案;二是如何在有限的水资源条件下寻求最有效的资源开发利用模式。

【例21-1】 有甲、乙两个水库同时向A、B、C三个城市供水,单位水费如表21-1所示。甲、乙水库的日供水能力为28万m3/d和35万m3/d,A、B、C三个城市的日需水量分别为10万m3/d、15万m3/d和20万m3/d。试确定满足三个城市用水需求条件下使输水费用最小的水资源分配方案。

表21-1　水库单位输水费用　单位:元/m3

解:设甲水库向三城市日供水量分别为x11、x12、x13,乙水库向三城市供水量分别为x21、x22、x23,则供水量满足下述约束条件:

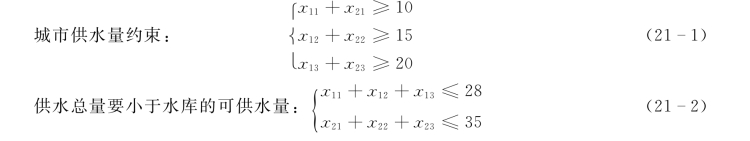
水库向各个城市供水量应大于等于零,即

并使输水总费用最小:

【例212】 水库可分配水资源量为5个单位,拟供给甲乙两个灌区,两灌区的最大需水量分别为4个单位和3个单位,当两个灌区单位水量可获得的灌溉效益分别为2和3时,问如何配水可以使获得的效益最大?

解:设甲乙两个灌区分配的水量分别为x1和x2两个单位,则该问题满足下述约束条件:

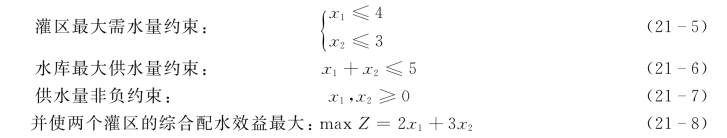
2.线性规划的数学模型

设X=(x1,x2,…,xn)T为n维实欧氏空间E n内的一点,则线性规划的数学模型可以写成下述一般形式:

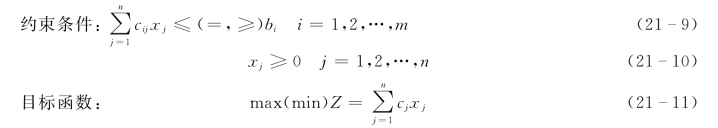
从上述例题及标准模型可知,对于一个实际的水资源优化配置问题建立LP数学模型时,需先根据问题条件要求选择一组非负的决策变量x1,x2,…,xn,然后按照问题要求建立目标函数关系式。根据客观条件的限制,如水资源量、供水工程规模、水环境标准等,建立约束方程,由此共同构成LP数学模型。目前情况下,线性规划模型的通用解法是单纯形法、修正单纯形法、对偶单纯形法、多项式算法等。由于具体的解法过程复杂、内容太长,限于篇幅原因,本节就不介绍具体的模型解答过程了。

(二)动态规划

动态规划(Dynamic Programming,简称DP)是20世纪50年代初期由美国数学家贝尔曼等人提出并逐渐发展起来的数学分支,它是一种解决多阶段决策过程最优化的数学规划法。DP的数学模型和求解方法比较灵活,无论对于系统是连续或离散的、线性或非线性的、确定性的或随机性的,只要能构成多阶段决策过程,便可以用DP推求其最优解。因而在水资源系统分析领域具有广泛的应用,比LP、NLP等方法更有成效。它在广泛应用中的主要障碍是“维数灾”。

1.动态规划的基本原理与思路

在客观事物中,存在这么一类问题:可以按照时间或空间特性将其划分为若干个互相联系的阶段;在每个阶段都需要做出决策,并且一个阶段的决策将影响下阶段的状态;所有阶段决策构成一个决策序列,称为策略;每个策略都对应一个效果;所选择的策略应该使整个过程获得最优结果。这类问题称为多阶段决策过程,DP就是按照上述思路寻求问题最优解的工具。由于各阶段决策与时间进程有关,故称为动态规划。当DP应用在水资源优化配置中,例如水库的优化调度、以灌溉为目标的年调节水库调度问题,就是一个运用最优化原理进行控制的多阶段决策过程。一年可以按时间分为若干阶段,在每个阶段,以水库蓄水量(或者水位)为状态变量,以放水量为决策变量,把灌溉效益作为目标函数。在满足约束条件下确定各个阶段的放水量,即组成一个决策序列。如果所选定的各时段放水量能使全年灌溉效益最大,这就是一个最优策略,即最优调度方案。(董子敖,1989;许自达,1984)

(1)多阶段决策过程。设某系统随空间或时间变化,其演变过程可以划分为若干个阶段,系统在各个阶段的状态由状态序列{s1,s2,…,sn,sn+1,…,sN+1}来表征。若n+1阶段的状态sn+1是由n阶段的状态sn经过转移而形成,即

该式称为状态转移方程。并且这种转移是在一定约束下进行选择的,则相应状态转移的选择就是决策dn,转移过程就是决策的结果。每个阶段都要做出一种决策,从而使整个过程获得最优结果。这一过程就称为多阶段决策过程,或称为序列过程,如图21-1所示。因此,多阶段决策过程应看成是阶段、状态、决策以及和它们相关联的效果的综合体。

(2)最优化原理与递推方程。作为水库优化调度的多阶段决策过程,在供水期初与供水期末之间各个阶段可有许多状态和不同决策,构成众多的策略,即有众多的调度方案。如果采用枚举法,逐一计算各个方案的总效益,从而选择总效益为最大的优化调度方案,显见是非常繁琐甚至是难以实行的。鉴于枚举方案的不可行性,DP以最优化原理为基础,在此基础上使用递推方程作为DP的基本方程,来解决动态规划问题。

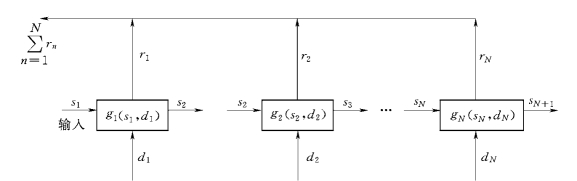
图21-1　N阶段决策过程的状态转移图

最优化原理是贝尔曼提出的DP的基本原理,其表述为:“一个过程的策略具有这样的性质,即不论初始状态和初始决策如何,对于初始决策所构成的下一个状态来说,其后的所有决策必须构成一个最优策略”。而动态规划法的求解过程正是基于此原理,把一个具体问题表述为使过程状态序贯转移,相应效益指标函数递推变化的递推方程,即利用n阶段与n+1阶段间的如下关系:

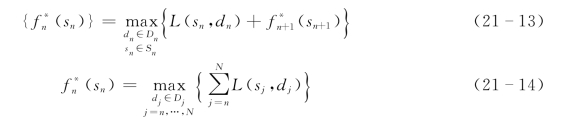
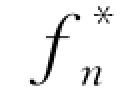(sn)表示对由任一阶段n上的任一可行状态sn开始的后部子过程(余留过程),使用可行决策序列dj,所得到的最大效益。L(sn,dn)表示每一阶段的效益。

总之,用DP求解问题时,要首先选定系统状态转移方向,该方向可以与系统实际运动方向一致,也可以相反。然后逆着选定的系统状态转移方向,使用递推方程由计算用的终端向始端进行递推计算,逐阶段地找出最优决策。这种规划过程称为“逆序”决策过程。

2.动态规划的数学模型与解法

DP的数学模型一般由系统方程、目标函数、约束条件和边界条件等几个部分组成。在建立模型时,首先将研究的问题根据其时间或空间特点划分阶段,形成多阶段决策过程,并相应的选取阶段变量、状态变量和决策变量。

(1)动态规划的数学模型。

1)系统方程。系统方程即上面所说的状态转移方程,它是包括阶段变量、状态变量和决策变量三种变量的一组关系式。对于具有一个状态变量、一个决策变量的一维多阶段决策过程,系统方程可以写为:

式中:sn为阶段n的状态变量;dn为阶段n的决策变量;g(sn,dn)为状态转移函数。

例如单一水库调度问题,由于其属于一维状态,其系统方程就可以直接写为:

式中:sn、sn+1为n时段和n+1时段初水库蓄水量;In、dn、Wn为n时段内水库来水量、放水量和蒸发渗漏损失量。

对于多水库、多时段优化调度的水资源配置来说,相当于具有m维状态向量、q维决策向量的系统,方程可以写为:

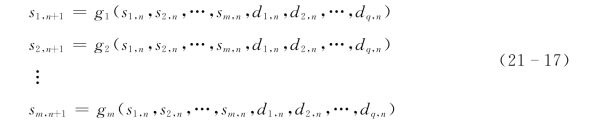
2)目标函数。DP和其他数学规划方法一样,其数学模型同样要包括目标函数。目标函数的最优准则可以是效益最大化,也可以是费用最小化或其他指标。目标函数值决定于系统中的状态变量和决策变量,设以F表示目标函数,则

式中:L为每一阶段的效益(或费用);F为系统的总效益(或总费用)。

若为灌溉效益最大化目标函数,则

若为消耗费用最小化目标函数,则

3)约束条件。对状态变量和决策变量的约束可以根据实际的限制条件给出。(www.xing528.com)

第n阶段的状态向量sn约束于集合Sn,记为:

式中:Sn为第n阶段的可行状态集合。

在第n阶段状态sn时所采用的决策向量dn约束于集合Dn(sn),记为:

4)边界条件。指初始状态:

或终末状态:

式中:C1和CN均为已知常数。

DP就是要在系统方程、约束条件、边界条件约束下寻求目标函数最优值和相应的最优决策序列。

动态规划并没有固定的标准解法程序,主要是重复使用递推方程,逐段寻优。由递推方程21-13可知,动态规划法实质上就是将一个n阶段决策过程的实际问题,化为n个形式与性质相同而又相互联系的单阶段决策的子问题。每个子问题又都是求变量极值,于是重复地解n个比较简单的求极值问题,逐步保留子问题的最优策略而求得全周期的最优策略。

需要指出的是,尽管动态规划法适用于解决各种各样的多阶段决策过程问题,但是当变量个数较多的时候,需要冗长的计算时间和很大的计算机内存,如下式表示:

式中:Ti为第i状态变量的离散点数;m为状态向量维数,即状态变量个数。

设Ti均等于100,当m=5时,Tn=1010,这个数目已经超过现有一般计算机的内存能力。因此,我们需要寻求降维的算法。目前的解法大体上有:格点法、拉格朗日乘数法(函数近似法)、逐次逼近法和增量动态规划法等。而根据输入的不同又有确定性动态规划、随机性动态规划和模糊动态规划等。

(2)实例分析。

【例21-3】 某灌区内有N种作物,自水库引水灌溉,在中等干旱年,水库可提供水量为Q,如以水量xn供给第n种作物,所得到的净效益为rn(xn)。问水资源Q在N种作物之间如何分配,才能使总的净效益最大。

解:这是一个具有N个决策变量的最优分配问题,由于灌溉水量与其所产生的效益之间的非线性关系较为复杂,而且某个阶段的一种作物的用水量直接影响了后一阶段另一作物的用水量,所以该问题是一个动态的多阶段水资源优化配置决策问题,这样便可以使用DP求解。

1)阶段变量。每种作物作为一个用水单位,可以看作一个阶段,共有N个阶段,阶段变量n=1,2,…,N。

2)状态变量和决策变量。状态变量为各个阶段可用于分配的有效水量,以q表示;决策变量为供给每种作物的水量,即各阶段的供水量,以xn表示。

3)系统方程。根据状态变量和决策变量之间关系推得该问题的系统方程(即状态转移方程)为:

4)目标函数。设F*(Q)为以水资源Q分配给N种作物而获得的最大总净效益,则:

5)约束条件。供给各种作物水量之和不超过水资源总量Q

供给第n种作物的水量xn不能超过在第n阶段可用于分配的有效水量,而且非负数

qn不能超过水资源总量Q,也是非负数

6)初始条件。

采用逆序递推求解上述数学模型,其递推方程为

此例是一个一维求效益最大值的问题,按照递推方程的算法,编程即可求得本例的最优分配方案,具体计算过程不再赘述。

(3)求解算法—逐次优化算法。逐次优化算法(The Progressive Optimization Algorithm,简称POA),由Howson和Sancho(1975)提出,也是求解多阶段决策问题的一种优化方法。这种方法是对多阶段动态规划在计算上的改进,能达到动态规划的求解目的。同时,在对大系统多目标问题进行求解时,避免了“维数灾”障碍。

逐次优化算法的原理为:“最优路径具有这样的特性,每次决策集合相对于它的初始值和终止值来说都是最优的”。水库调度过程是“完全各态历经的马尔柯夫过程”(杨侃等,1996)。优化后的稳定调度线与初始状态无关。算法的主要思想是将一个多阶段的决策过程划为一系列相对独立的二阶段过程,并按一定顺序或时序,从第一个或最后一个阶段开始,逐次求出相邻两阶段的最优决策,并经历各阶段,从而得出整个系统的最优决策。

应用动态规划法时,要将状态空间离散化,若划分过细,会出现“维数灾”的问题。POA法的寻优思路与动态规划法较为相似,但又严格区别于动态规划法,它是将一个多阶段的决策过程划为一系列相对独立的二阶段优化过程,并按一定顺序或时序,从第一个或最后一个阶段开始,逐次求出相邻两阶段的最优决策,并经历各阶段,从而得到整个系统的最优决策。POA算法概念明确,使用简便,不需离散状态变量,因而计算速度快,且不会出现“维数灾”。(王浩等,2002)

(三)多目标优化

水资源系统优化管理过程中所面临的决策问题,大多存在着多个不同目标,目标之间既“不可公度”又常常相互矛盾,属于多目标决策(Multi-objective Decision Masking)问题。由于多目标决策问题不存在类似单目标优化问题那样的最优解,只存在着非劣解,决策者根据其偏好在非劣解中选择满意解或最佳均衡解,从而使得前述单目标决策方法因忽视了客观事物普遍存在的多目标性而存在局限性。因此,有必要运用多目标决策理论和方法研究许多多目标水资源优化决策问题。下面我们通过一个简化了的水库优化调度模型简单地介绍多目标优化模型的应用。

多目标优化问题是向量优化问题,其解为非劣解集。解决多目标优化的基本思想,是将多目标问题化为单目标问题,进而使用较为成熟的单目标优化技术。将多目标转为单目标一般有多种方法,可归纳为以下三类途径:①评价函数法。它是根据问题的特点和决策者的意图,构造一个把多个目标转化为单个目标的评价函数,化为单目标优化问题。这类方法有:线性加权和法、极大极小法、理想点法等。②交互规划法。它是一类不直接使用评价函数的表达式,而是以分析者和决策者始终交换信息的人机对话式求解过程。这类方法有:逐步宽容法、权衡比较替代法、逐次线性加权和法等。③混合优选法:对于同时含有极大化和极小化目标的问题,可以将极小化目标转化为极大化目标再求解。但也可以不转换,而采用分目标乘除法、功效函数法和选择法等直接求解。

【例21-4】 某水库为多目标综合利用水资源系统,其优化调度应使系统达到城市供水量最大、灌溉缺水量最小、年发电量最大和弃水量最小等目标要求。据此,可拟定以下3个目标函数:

城市供水目标:

农业灌溉目标:

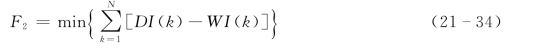
年发电量目标:

式中:WC(k)、WI(k)分别为城市和灌溉供水;DI(k)为灌溉需水量;N(k)为年发电量。对于上述水库兴利优化调度模型,如果直接采用多维多目标动态规划或其他方法求解,则可能因为目标、状态、和决策变量较多地占用计算机内存和时间,因而有必要先做适当处理,将多目标问题转化为单目标,再进行求解。考虑到城市供水的要求保证率最高,灌溉用水要求保证率略微降低,而水库发电的要求级别相对较低,因此将水库优化调度目标定为年城市供水量最大(式21-33),而将水库发电量与灌溉供水当作约束条件进行处理。

这样,水库优化调度的目标函数就可以描述为:在满足水库蓄水要求、水库发电规划目标与农业用水保证率条件下,使水库的城市供水量最大。

除了以上通过调整目标函数,将两个目标函数转化为约束条件的方法之外,该模型还可以通过将3类目标函数转化为用货币指标表示的经济目标,如水资源综合利用净效益最大、水库运行费用最小等。理论上,在水资源多目标优化分析过程中,最理想的目标被公认为经济准则。但是理想的经济目标往往在实际中难以用货币尺度合理度量,因此目前在资源系统优化配置中也经常用的是非经济目标,如供水量最大、弃水量最小、供水系统运行费用最小等。虽然非经济目标不尽合理,但概念明确,计算简便,使用方便。