复数的基本运算的分析介绍

对正弦交流电路进行分析，就需要对正弦量进行加、减、乘、除运算。用一般的运算方法比较烦琐，但用数学中的复数概念，可以方便地解决正弦量之间的计算问题。

1.复数的表示

1）代数表示

复数在数学中的代数形式用A＝a＋bi表示。其中a为实部，b为虚部，，称为虚单位。但在电工学中，i已表示电流，为避免混淆，复数常用A＝a＋jb表示。

2）图形表示

取一个直角坐标系，横轴称实轴，用来表示复数的实部；纵轴称虚轴，用来表示复数的虚部。两轴所在的平面称为复平面。对每一个复数而言，都可以在这个复平面上找到唯一对应的点；反过来，每一个复平面上的点可以对应唯一的一个复数。

复数还可以用复平面上的矢量来表示。

例6－1　在图6－1中标出复数5＋j4对应复平面上的点P1，以及复数－4＋j3对应的点P2和复数－3－j2对应的点P3。同时用复矢量来表示复数5＋j4和－4＋j3。

标注方法：

在横轴上找对复数的实部分量，在纵轴上找对复数的虚部分量，并分别作虚线，如5＋j4示例。两线的交点即复数在复平面上唯一对应的点（请读者自行标注3个点于图6－1中）。从原点0指向该点的矢量即为复矢量。

由以上示例可知，任意一个复数A＝a＋jb都可以对应一个复矢量OP，如图6－2所示。矢量的长度r称为复数的模，模总取正值。矢量与实轴正方向的夹角θ，称为复数A的幅角。它们和复数的实部、虚部分量之间满足

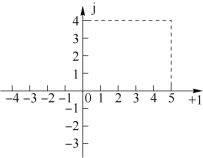
图6－1　复数与复平面上对应的点

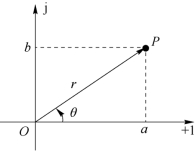
图6－2　复矢量表示复数

根据三角函数关系，可知

a是复数A的实部，也是复数A的模在实轴上的投影；b则是它的虚部，也是该复数的模在虚轴上的投影。

因而复数也可以写成

式（6－4）指出，复数除了有代数表示形式外，还有三角函数的表示形式，它与代数形式的转换关系满足式（6－1）和式（6－2）及式（6－3）。

2.复数的形式

复数除了代数形式、三角函数形式外，根据欧拉公式，即

式（6－4）又可以写成

该形式称为复数的指数形式。

对应于极坐标，复数还可以写成

例6－2　写出复数5＋j4和复数－3－j2的三角函数形式、指数形式和极坐标形式。

解：（1）5＋j4的模

5＋j4的幅角

则其三角函数形式为：6.4cos38.7°＋j6.4sin38.7°

指数形式为：6.4ej38.7°

极坐标形式为：6.438.7°

（2）－3－j2的模

－3－j2的幅角θ＝arctan

直接求反函数可得角度33.7°。由于复数－3－j2的矢量位于第三象限，如例6－1中应标注的位置，因此利用tan（π＋α）＝tanα，以及三角函数中正负角度的概念，将幅角写成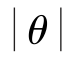≤180°的形式，最终确定幅角θ＝－146.3°

则其三角函数形式为：3.6cos（－146.3°）＋j3.6sin（－146.3°）

指数形式为：3.6ej（－146.3°）

极坐标形式为：

例6－3　写出－1、j、－2j的极坐标形式。

解：－1的虚部为零，对应的矢量与复平面上横轴的负半轴重合，其极坐标形式为：

同理，j的实部为零，其矢量与复平面上纵轴的正半轴重合，其极坐标形式为：(www.xing528.com)

－2j的矢量与复平面上纵轴的负半轴重合，模为2，其极坐标形式为：

练一练：

写出复数－4＋j3的三角函数形式和极坐标形式。

（1）计算复数的模。

（2）计算复数的幅角，注意复矢量所在的象限。

（3）写出复数的三角函数形式。

解题微课

（4）写出复数的极坐标形式。

3.复数的运算

1）复数的加、减法

例6－4　有两复数求A－B。

解题步骤如下。

（1）两个极坐标形式的复数之间做减法。如果直接按极坐标反映的矢量形式相减，则并不简便。因而要先将复数化作代数形式。

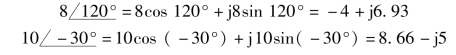
（2）两者代数相减。

（3）将代数形式的结果转换回极坐标形式。

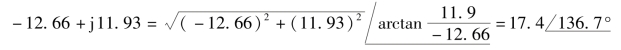
通过上述举例可知，复数要化为代数形式相加减。现设有两个复数：

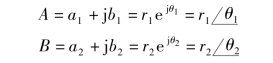
在复数相加减时，将实部与实部相加减，虚部与虚部相加减。因此，有

2）复数的乘、除法

例6－5　有两复数A＝8＋j6，B＝6－j8。求A·B与A/B。

解题步骤如下。

（1）两个代数形式的复数做乘除法。若直接乘除，则不简便，因而先将复数化作极坐标形式。

（2）复数相乘：模相乘，幅角相加。

（3）复数相除：模相除，幅角相减。

通过上述举例可知，复数要化为极坐标形式相乘除。在乘除时，模与模相乘除，幅角与幅角相加减。如式（6－8）和式（6－9），即

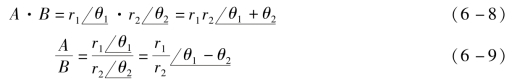
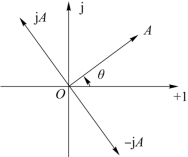
图6－3　例6－6矢量图

三者的矢量图如图6－3所示。

通过该例题可知，一个复数乘以j，相当于把这个复数矢量在复平面逆时针方向旋转了90°；而乘以－j，则相当于把该矢量顺时针方向旋转了90°。同理可知，当一个复数乘以－1时，相当于将该复数矢量旋转了180°。

像这样模等于1、幅角为θ的复数，当它与其他任意复数相乘时，都不会改变模的值，但能改变幅角。实际上就是将该任意复数的复矢量从原来位置逆时针方向旋转了θ角。用来表示这种模为1的复数，并称它们为旋转因子。

练一练：

有两复数，求I1＋I2和I1I2。

（1）将两复数转换成代数形式。

（2）复数相加。

（3）复数相乘。