流动应力方程简介

有限元法被广泛应用于复杂的金属成形过程分析，例如大变形、基于变形历史和复杂接触边界的大变形问题。在求解过程中，须将材料的真实应力-应变曲线写成数学表达式，即流动应力方程，也称作本构方程。在确定流动应力方程时应尽可能符合材料的实际情况，同时表达式应尽可能简单，以便求解复杂的实际问题时不会出现大的数学困难。

众所周知，应力应变关系曲线通常包括两个部分：一个是线弹性部分；另一个是非线性的塑性变形部分。目前已有许多近似的本构方程被用来描述材料的应力应变曲线，其中式（5-11）～式（5-17）被广泛地应用于金属成形过程模拟，这些方程适用于低应变速率和常温下的变形过程，即忽略了在塑性变形过程中由温度升高带来的对流动应力的影响。

Hollomon方程为 σ＝Kεⁿ （5-11）

Ludwik方程为 σ＝σ₀+Kεⁿ （5-12）

Swift方程为 σ＝a（ε-b）ⁿ （5-13）

Voce方程为 σ＝σ_s-（σ_s-σ₀）e^-nε （5-14）

Samanta方程为 σ＝σ₀+cln ε （5-15）

Hockett-Sherby方程为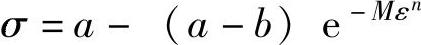 （5-16）

Ghosh方程为 σ＝a（b+ε）ⁿ-c （5-17）

在上述流动应力方程中，有许多待定常数，这些未知数可以通过材料的拉伸实验来确定。最普遍的拉伸实验即单向拉伸实验，它通过在一个普通的拉伸测试机器上用同种条件下的单轴加载，然后用伸长计测量某一固定标距内的试件伸长量来实现。这种测量的缺点是它假设的材料均匀性只在达到最大载荷前才满足，在达到最大载荷后会发生塑性失稳和应力集中，进而产生分散性缩颈，最终导致试件断裂。而在薄板变形时往往集中性失稳才是导致破裂的主因，当试件的宽度下降时出现分散性失稳而非集中性失稳，事实上集中性失稳发生时试件的宽度减薄量很小，而在失稳的区域厚度变化却非常剧烈，很快发生破裂。为了精确地描述材料的这一变形行为，人们想到了一些特殊的方法，例如J.Kajberg通过对平面内位移场逐点进行数字散斑摄影（DSP）来捕捉材料的变形过程，然后在假设体积不可压缩的情况下，由微分方法得到塑性应变。通过运用逆向模型，包括对单向拉伸实验的有限元分析，而使材料参数逼近目标函数的最小值，这个目标函数是基于实验和有限元计算所得的位移和应变场的差值。(www.xing528.com)

下面分别用式（5-11）～式（5-17）中的流动应力方程对热轧酸洗钢板QStE340TM的单向拉伸真实应力应变曲线进行拟合。以Hollomon流动应力方程为例，其拟合步骤为：用软件OriginPro7.5对材料的单向拉伸所得到的真实应力应变值进行拟合，可得到两个参数值——K、n，然后代入σ＝Kεⁿ，可得到一个以ε为自变量，σ为因变量的关系式。从而给定一个ε的变化区域，就能绘制出一条应力应变曲线。以同样的方式拟合出其他六种方程中的待定系数项，可以得到七条曲线。与实验值作比较，即得到图5-2～图5-4。

可以看到，从屈服到强度极限的一段，除45度方向的Samanta方程拟合结果有些差别，各方程得到的拟合结果都十分相近。过了强度极限后，Voce曲线逐渐趋向水平，Hockett-Sherby与Samanta变化也趋于平缓。

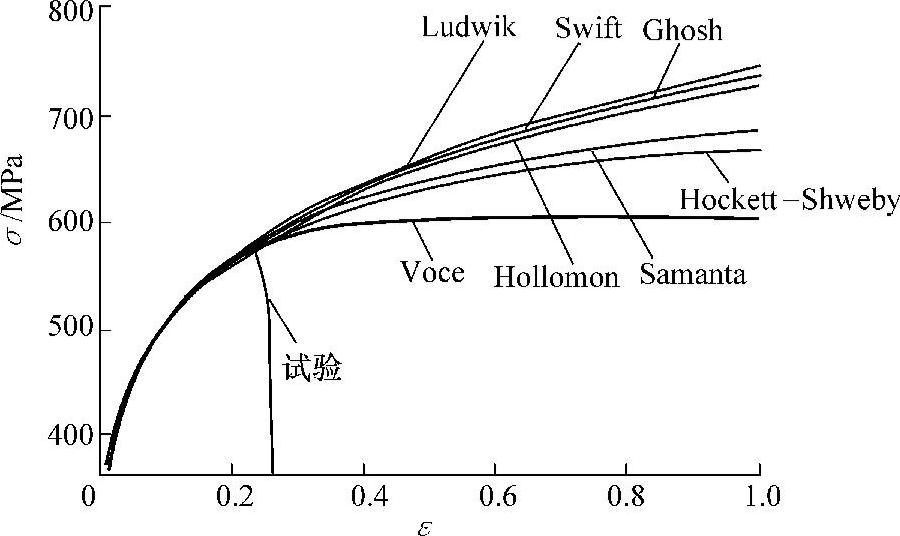
图5-2 不同本构方程对与轧制方向成0°的QStE340TM试件单向拉伸数据的拟合

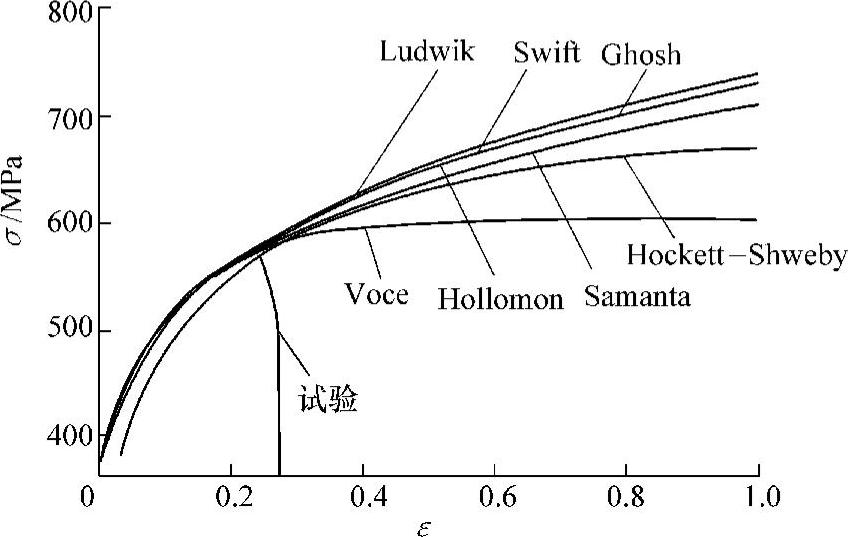
图5-3 不同本构方程对与轧制方向成45°的QStE340TM试件单向拉伸数据的拟合

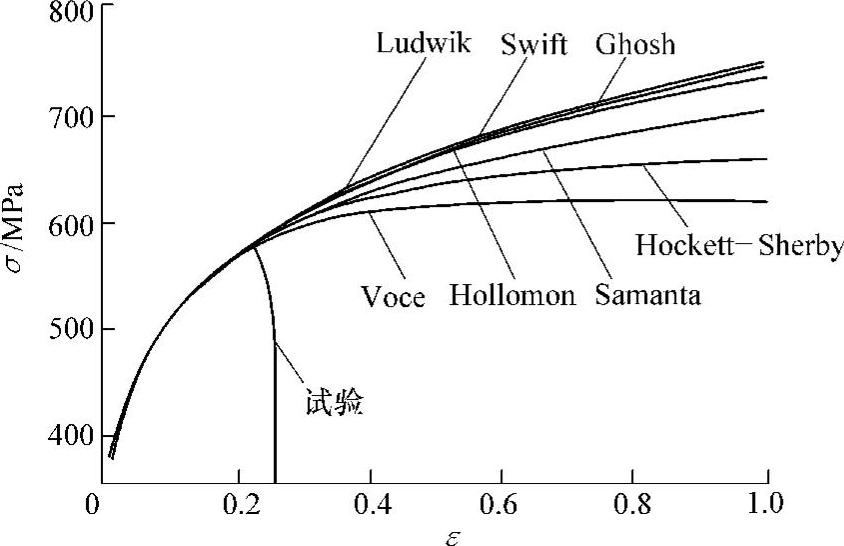
图5-4 不同本构方程对与轧制方向成90°的QStE340TM试件单向拉伸数据的拟合

由图5-2～图5-4可知，在变形量较小时，不同流动应力方程的区别并不明显，但对于大变形过程，流动应力方程的选取将会对计算结果产生影响。